5  Primeiras extensões aos tipos básicos do C++

Quando se fala de uma linguagem de programação como o C++ não se fala apenas da linguagem em si, com o seu léxico, sintaxe, gramática e semântica.  Fala-se também de um conjunto de ferramentas acessíveis ao programador que, não fazendo parte da linguagem propriamente dita, estão acessíveis em qualquer implementação da linguagem.  Ao conjunto dessas ferramentas adicionais chama-se biblioteca padrão (standard library).  Dela fazem parte, por exemplo, os canais cin e cout, que permitem leituras e escritas do teclado e para o ecrã.  Assim, em rigor, o programador tem à sua disposição não apenas o C++ em si mas o C++ equipado com a biblioteca padrão.  Para o programador, no entanto, tudo funciona como se a linguagem em si incluísse essas ferramentas.  Isto é, para o programador o que está acessível não é o C++, mas um "C++ ++" de que fazem parte todas as ferramentas da biblioteca.

A tarefa de um programador é resolver problemas, usando um computador (pelo menos), através da escrita de programas numa linguagem de programação dada.  Depois de especificado o problema com exactidão, o programador inteligente começa por procurar, na linguagem básica, na biblioteca padrão e noutras quaisquer bibliotecas existentes, ferramentas que resolvam o problema na totalidade ou quase: esta procura evita as perdas de tempo associadas ao reinventar da roda ainda infelizmente tão em voga *.  Se não existirem ferramentas disponíveis, então há que construí-las.  Ao fazê-lo, o programador está a expandir mais uma vez a linguagem disponível, que passa a dispor de ferramentas adicionais (digamos que "incrementa" de novo a linguagem para "C++ ++ ++").

Há essencialmente duas formas de construir ferramentas adicionais para uma linguagem.  A primeira passa por equipar a linguagem com operações adicionais, na forma de funções e procedimentos, usando os tipos existentes (e.g., int, char, bool ou double).  A segunda passa por adicionar tipos à linguagem.  Para que esses novos tipos tenham algum interesse, é fundamental que tenham operações próprias, que têm de ser concretizadas pelo programador.  Assim, a segunda forma de expandir a linguagem passa necessariamente pela primeira.

Neste capítulo ver-se-ão as formas mais básicas de acrescentar tipos, e respectivas operações, ao C++, nomeadamente através das matrizes (agregados de variáveis do mesmo tipo indexáveis por um índice) e dos enumerados (tipos que tomam um conjunto discreto, e normalmente pequeno, de diferentes valores).  No próximo capítulo abordar-se-ão as classes, que é o mecanismo por eleição no C++ para construção de novos tipos com o consequente aumento de funcionalidade da linguagem.

*  Por outro lado, é importante notar que se pede muitas vezes ao estudante que reinvente a roda.  Acontece que fazê-lo é um passo fundamental para o treino na resolução de problemas concretos.  Convém portanto que o estudante se disponha a essa tarefa que, fora do contexto da aprendizagem, é inútil.  Mas convém também que não se deixe viciar na resolução por si próprio de todos os pequenos problemas que já foram resolvidos milhares de vezes.  É importante saber fazer um equilíbrio entre a curiosidade intelectual de resolver esses problemas e o pragmatismo de procurar um solução já pronta.  Durante a vida académica, a balança deve pender fortemente no sentido da curiosidade intelectual.  Finda a vida académica,  o equilíbrio deve pender mais para o pragmatismo.

5.1  Enumerações ou tipos enumerados

Além dos tipos de dados pré-definidos no C++, os chamados tipos básicos, podem-se criar tipos de dados adicionais.  Essa é, como se verá mais tarde, uma das tarefas fundamentais da programação centrada nos dados.  Para já, abordar-se-ão extensões simples aos tipos do C++: os tipos enumerados.

Uma variável de um tipo enumerado pode conter um número limitado de valores, que se enumeram na definição do tipo.  Por exemplo:

enum DiaDaSemana {
    segunda_feira,
    terça_feira,
    quarta_feira,
    quinta_feira,
    sexta_feira,
    sábado,
    domingo
};
define um tipo enumerado com sete valores possíveis, um para cada dia da semana *.  O novo tipo utiliza-se como habitualmente em C++.  Pode-se, por exemplo, definir variáveis do novo tipo:
DiaDaSemana dia;
Pode-se atribuir atribuir à nova variável dia qualquer dos valores listados na definição do tipo enumerado DiaDaSemana:
dia = terça_feira;
Cada um dos valores associados ao tipo DiaDaSemana (viz. segunda_feira, ..., domingo) é utilizado no código C++ como um valor literal para esse tipo, tal como 10 é um valor literal do tipo int ou 'a' é um valor literal do tipo char.  Como se trata de um tipo definido pelo utilizador, não é possível, sem mais esforço, ler valores desse tipo do teclado ou escrevê-los no ecrã usando os métodos habituais (viz. os operadores de extracção e inserção em canais: cin >> e cout <<).  Mais tarde ver-se-á como se pode "ensinar" o computador a ler e escrever tipos enumerados de dados (Secção 7.3).

Na maioria dos casos os tipos enumerados são usados para tornar mais claro o significado dos valores atribuídos a uma variável, pois segunda_feira tem claramente mais significado que 0!  Mas, na realidade, os valores de tipos enumerados são representados como inteiros atribuídos sucessivamente a partir de zero.  Assim, segunda_feira tem representação interna 0, terça_feira tem representação 1, etc.  De facto, se se tentar imprimir segunda_feira o resultado será 0, que é a sua representação na forma de um inteiro.  É possível atribuir inteiros arbitrários a cada um dos valores de uma enumeração, pelo que podem existir representações idênticas para valores com nome diferentes:

enum DiaDaSemana { // agora com nomes alternativos...
    primeiro = 0,  // inicialização redundante: o primeiro valor é sempre 0.
    segunda = primeiro,
    segunda_feira = segunda,
    terça,
    terça_feira = terça,
    quarta,
    quarta_feira = quarta,
    quinta,
    quinta_feira = quinta,
    sexta,
    sexta_feira = sexta,
    sábado,
    domingo,
    último = domingo,
};
Se um operando de um tipo enumerado ocorrer numa expressão, o C++ geralmente convertê-lo-á num inteiro.  Essa conversão também se pode explicitar, escrevendo int(segunda_feira), por exemplo.  As conversões opostas também são possíveis, usando-se DiaDaSemana(2), por exemplo, para obter quarta_feira.  Na próxima secção ver-se-á como redefinir os operadores do C++ para operarem sobre tipos enumerados sem surpresas desagradáveis para o programador (que acontece quando se incrementa uma variável do tipo DiaDaSemana que contém o valor domingo?).

* Na realidade os enumerados podem conter valores que não correspondem aos especificados na sua definição [1, página 77].

5.2  Sobrecarga de operadores

Da mesma forma que se podem sobrecarregar nomes de funções, i.e., dar o mesmo nome a funções que, tendo semanticamente o mesmo significado, operam com argumentos de tipos diferentes (ou em diferente número), também é possível sobrecarregar o significado dos operadores usuais do C++ de modo a que tenham um significado especial quando aplicados a tipos definidos pelo utilizador.  Se se pretender, por exemplo, sobrecarregar o operador ++ prefixo (incrementação prefixa) para funcionar com o tipo DiaDeSemana definido acima, pode-se definir um procedimento com uma sintaxe especial:
DiaDaSemana operator ++ (DiaDaSemana& dia)
{
    if(dia == último)
        return dia = primeiro;
    else
        return dia = DiaDeSemana(int(dia) + 1);
}
onde se substituiu o habitual nome da função (ou procedimento) pela palavra chave operator seguida do operador C++ a sobrecarregar *.

Assim, a incrementação de uma variável do tipo DiaDeSemana conduz sempre ao dia da semana subsequente.  Note-se que se utilizou primeiro e último e não segunda_feira e domingo, pois dessa forma pode-se mais tarde decidir que a semana começa ao Domingo sem ter de alterar o procedimento acima, alterando apenas a definição da enumeração.

Este tipo de sobrecarga, como é óbvio, só pode ser feito para novos tipos definidos pelo programador.  Esta restrição evita redefinições abusivas do significado do operador + quando aplicado a tipos básicos como o int, por exemplo, que poderiam ter resultados trágicos.

* Em todo o rigor o operador de incrementação prefixa deveria devolver uma referência para um DiaDaSemana.  Veja-se a secção Operador ++ prefixo para a classe Racional.

5.3  Matrizes

Muitas vezes é necessário guardar e manipular conjuntos de variáveis do mesmo tipo.  Se fosse necessário, por exemplo, calcular a média de três valores de vírgula flutuante introduzidos pelo utilizador de um programa e escrever cada um desses valores dividido pela média calculada, ter-se-ia de escrever:
#include <iostream>
using namespace std;

int main()
{
    // Leitura:
    cout << "Introduza três valores: ";
    double a, b, c;
    cin >> a >> b >> c;

    // Cálculo da média:
    const double média = (a + b + c) / 3.0;

    // Divisão pela média:
    a /= média;
    b /= média;
    c /= média;

    // Escrita do resultado:
    cout << a << ' ' << b << ' ' << c << endl;
}

Se se pretendesse dividir, já não três, mas 100 ou mesmo 1000 valores pela sua média, esta abordagem seria no mínimo pouco elegante, já que seriam necessárias tantas variáveis quantos os valores a ler do teclado.  A linguagem C++ resolve este tipo de problemas fornecendo o conceito de matriz (array em inglês): uma matriz é um agregado de elementos do mesmo tipo que podem ser indexados por valores inteiros.  Cada elemento de uma matriz pode ser interpretado e usado como outra variável qualquer.  A conversão do programa acima para ler 1000 em vez de três valores seria:
#include <iostream>

using namespace std;

int main()
{
    const int número_de_valores = 1000;

    // Leitura:
    cout << "Introduza " << número_de_valores << " valores: ";
    double valores[número_de_valores]; // definição da matriz com 1000 elementos
                                       // do tipo double.
    for(int i = 0; i != número_de_valores; ++i)
        cin >> valores[i];             // lê o i-ésimo valor do teclado.

    // Cálculo da média:
    double soma = 0.0;
    for(int i = 0; i != número_de_valores; ++i)
        soma += valores[i];            // acrescenta o i-ésimo valor à soma.
    const double média = soma / número_de_valores;

    // Divisão pela média:
    for(int i = 0; i != número_de_valores; ++i)
        valores[i] /= média;           // divide o i-ésimo valor pela média.

    // Escrita do resultado:
    for(int i = 0; i != número_de_valores; ++i)
        cout << valores[i] << ' ';     // escreve o i-ésimo valor.
    cout << endl;
}

Note-se a utilização de uma constante para representar o número de valores a processar.  Alterar o programa para processar não 1000 mas 10000 valores é, neste caso, trivial: basta redefinir a constante.  A alternativa seria fazer substituições automáticas no texto do programa, o que poderia ter consequências desastrosas se o valor literal 1000 fosse utilizado no programa num contexto diferente.

Note-se que o nome de uma constante atribui um significado a um valor.  Por exemplo, definir num programa de gestão de uma disciplina as constantes:

const int número_máximo_de_alunos_por_turma = 50;
const int peso_do_trabalho_na_nota_final = 50;
permite escrever o código sem qualquer utilização explícita do valor 50.  A utilização explícita do valor 50 obrigaria a inferir o seu significado exacto (número máximo de alunos ou peso do trabalho na nota final) a partir do contexto, tarefa que nem sempre é fácil e que se torna mais difícil à medida que os programas se vão tornando mais extensos.

5.3.1  Definição de matrizes

Para utilizar uma matriz de variáveis é necessário defini-la *.  A sintaxe da definição de matrizes em C++ é simples:
tipo nome[número_de_elementos];
em que tipo é o tipo de cada elemento da matriz, nome é o nome da matriz, e número_de_elementos é o número de elementos ou dimensão da nova matriz.  Por exemplo:
int mi[10];    // matriz com 10 int.
char mc[80];   // matriz com 80 char.
float mf[20];  // matriz com 20 float.
double md[3];  // matriz com 3 double.
O número de elementos de uma matriz tem de ser um valor conhecido durante a compilação do programa (i.e., um valor literal ou uma constante).  Não é possível (para já) criar uma matriz usando um número de elementos variável.  Mas é possível (e em geral aconselhável) usar constantes em vez de valores literais para indicar a sua dimensão:
int n = 50;
const int m = 100;
int matriz_de_inteiros[m];   // ok, m é uma constante.
int matriz_de_inteiros[300]; // ok, 300 é um valor literal.
int matriz_de_inteiros[n];   // errado, n não é uma constante.
Note-se que nem todas as constantes têm um valor conhecido durante a compilação: a palavra chave const limita-se a indicar ao compilador que o objecto a que diz respeito não poderá ser alterado.  Por exemplo:
// Valor conhecido durante a compilação:
const int número_máximo_de_alunos = 10000;
int alunos[número_máximo_de_alunos]; // ok.

int número_de_alunos_lido;
cin >> número_de_alunos_lido;
// Valor desconhecido durante a compilação:
const int número_de_alunos = número_de_alunos_lido;

int alunos[número_de_alunos]; // erro!

* Ou melhor, é necessário que ela esteja declarada, podendo a sua definição estar noutro local.

5.3.2  Indexação de matrizes

Seja a definição
int m[10];
Para atribuir o valor 5 ao sétimo elemento da matriz pode-se escrever:
m[6] = 5;
Ao valor 6, colocado entre [], chama-se índice.  Ao escrever numa expressão o nome de uma matriz seguido de [] com um determinado índice está-se a efectuar uma operação de indexação, i.e., a aceder a um dado elemento da matriz indicando o seu índice.

Os índices das matrizes são sempre números inteiros e começam sempre em zero.  Assim, o primeiro elemento da matriz m é m[0], o segundo m[1], e assim sucessivamente.  Embora esta convenção pareça algo estranha a início, ao fim de algum tempo torna-se muito natural.  Recorde-se os problemas de contagem de anos que decorreram de chamar ano 1 ao primeiro ano de vida de Cristo e a consequente polémica acerca de quando ocorre de facto a mudança de milénio *...

Como é óbvio, os índices usados para aceder às matrizes não necessitam de ser constantes: podem-se usar variáveis, como aliás se pode verificar no exemplo da leitura de 1000 valores apresentado atrás.  Assim, o exemplo anterior pode-se escrever:

int a = 6;
m[a] = 5; // atribui o inteiro 5 ao 7º elemento da matriz.
Usando de novo a analogia das folhas de papel, uma matriz é como um bloco de notas em que as folhas são numeradas a partir de 0 (zero).  Ao se escrever m[6] = 5, está-se a dizer algo como "substitua-se o valor que está escrito na folha 6 (a sétima) do bloco m pelo valor 5".  Abaixo mostra-se uma representação gráfica da matriz m depois desta atribuição (por ? representa-se um valor arbitrário, também conhecido por "lixo"):
Gráfico de matriz

Porventura uma das maiores deficiências da linguagem C++ está no tratamento das matrizes, particularmente na indexação.  Por exemplo, o código seguinte não resulta em qualquer erro de compilação nem tão pouco na terminação do programa com uma mensagem de erro, isto apesar de tentar atribuir valores a posições inexistentes da matriz (as posições com índices -1 e 4):

int a = 0;
int m[4];
int b = 0;
m[-1] = 1;  // erro! só se pode indexar de 0 a 3!
m[4] = 2;   // erro! só se pode indexar de 0 a 3!
cout << a << ' ' << b << endl;
O que aparece provavelmente escrito no ecrã é, em alguns compiladores, 
2 1
ou, noutros compiladores, 
1 2
dependendo da arrumação que o compilador dá às variáveis a, m e b na memória.  O que acontece é que as variáveis são arrumadas na memória (neste caso na pilha ou stack) do computador por ordem de definição, pelo que as "folhas de papel" correspondentes a a e b seguem ou precedem (conforme a direcção de crescimento da pilha) as folhas do "bloco de notas" correspondente a m.  Assim, a atribuição m[-1] = 1; coloca o valor 1 na folha que precede a folha 0 de m na memória, normalmente a folha de b (a pilha normalmente cresce "para baixo", como se verá na disciplina de Arquitectura de Computadores).

Esta é uma fonte muito frequente de erros no C++, pelo que se recomenda extremo cuidado na utilização de matrizes.  Uma vez que muitos ciclos usam matrizes, este é mais um argumento a favor do desenvolvimento disciplinado de ciclos e da explicitação de asserções (ver Usando instruções de asserção).

* Note-se que o primeiro ano antes do nascimento de Cristo é o ano -1: não há ano zero!  O problema é mais frequente do que parece.  Em Portugal, por exemplo, a numeração dos andares começa em R/C, ou zero, enquanto nos EUA começa em um (e que número terá o andar imediatamente abaixo?).  Ainda no que diz respeito a datas e horas, o primeiro dia de cada mês é 1, mas a primeira hora do dia (e o primeiro minuto de cada hora) é 0.  E já agora, porque se usam as expressões "de hoje a oito dias" e "de hoje a quinze dias" em vez de "daqui a sete dias" ou "daqui a 14 dias"?  Ou será que "amanhã" é sinónimo de "de hoje a dois dias" e "hoje" o mesmo que "de hoje a um dia"?

5.3.3  Inicialização de matrizes

Tal como para as variáveis simples, também as matrizes só são inicializadas implicitamente quando são estáticas *.  Matrizes automáticas, i.e., locais a alguma função (e sem o qualificador static) não são inicializadas: os seus elementos contêm inicialmente valores arbitrários (vulgo lixo).  Mas é possível inicializar explicitamente as matrizes.  Para isso, colocam-se os valores com que se pretende inicializar os elementos da matriz entre {}, por ordem e separados por vírgulas.  Por exemplo:
int m[4] = {10, 20, 0, 0};
O C++ permite ainda que se especifiquem menos valores de inicialização do que o número de elementos da matriz.  Nesse caso, os elementos não inicializados são automaticamente inicializados com 0 (zero), ou melhor, com o valor por omissão correspondente ao seu tipo (o valor por omissão dos tipos aritméticos é zero, o dos booleanos é falso, o dos enumerados é zero, mesmo que este valor não seja tomado por nenhum dos seus valores literais enumerados, e o das classes, ver Secção 6.4.7, é o valor construído pelo construtor por omissão).  Ou seja,
int m[4] = {10, 20};
tem o mesmo efeito que a primeira inicialização.  Pode-se aproveitar este comportamento algo obscuro para forçar a inicialização de uma matriz inteira com zeros:
int grande[100] = {}; // inicializa toda a matriz com 0 (zero).
Mas, como este comportamento é tudo menos óbvio, recomenda-se que se comentem bem tais utilizações.

Quando a inicialização é explícita, o C++ permite que se omita a dimensão da matriz, sendo esta inferida a partir do número de inicializadores.  Por exemplo:

int m[] = {10, 20, 0, 0};
tem o mesmo efeito que as definições anteriores.

* Na realidade as variáveis de tipos definidos pelo utilizador ou os elementos de matrizes com elementos de um tipo definido pelo utilizador (com excepção dos tipos enumerados) são sempre inicializadas, ainda que implicitamente (nesse caso são inicializadas com o construtor por omissão, ver Secção 6.4.7).  Só variáveis automáticas ou elementos de matrizes automáticas de tipos básicos do C++ ou de tipos enumerados não são inicializadas implicitamente, contendo por isso lixo se não forem inicializadas explicitamente.

5.3.4  Matrizes multidimensionais

Em C++ não existe o conceito de matrizes multidimensionais.  Mas a sintaxe de definição de matrizes permite a definição de matrizes cujos elementos são outras matrizes, o que acaba por ter quase o mesmo efeito prático.  Assim, a definição: 
int m[3][4];
é interpretada como significando int (m[3])[4], o que significa "m é uma matriz com três elementos, cada um dos quais é uma matriz com quatro elementos inteiros".  Ou seja, graficamente:

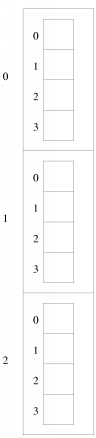
Embora sejam na realidade matrizes de matrizes, é usual interpretarem-se como matrizes multidimensionais (de resto, será esse o termo usado daqui em diante).  Por exemplo, a matriz m acima é interpretada como:











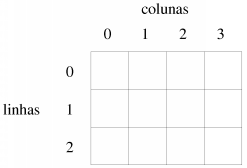
A indexação destas matrizes faz-se usando tantos índices quantas as "matrizes dentro de matrizes" (incluindo a exterior), ou seja, tantos índices quantas as dimensões da matriz.  Para m conforme definida acima:

m[1][3] = 4;       // atribui 4 ao elemento na linha 1, coluna 3 da matriz.
int i = 0, j = 0;
m[i][j] = m[1][3]; // atribui 4 à posição (0,0) da matriz.
A inicialização destas matrizes pode ser feita como indicado, tomando em conta, no entanto, que cada elemento da matriz é por sua vez uma matriz e por isso necessita de ser inicializado da mesma forma.  Por exemplo, a inicialização:
int m[3][4] = {
    {1, 2, 3, 4},
    {5, 6}
};
leva a que o troço de programa *
for(int i = 0; i != 3; ++i) {
    for(int j = 0; j != 4; ++j)
        cout << setw(2) << m[i][j];
    cout << endl;
}
escreva no ecrã
 1 2 3 4
 5 6 0 0
 0 0 0 0
* O manipulador setw() serve para indicar quantos caracteres devem ser usados para escrever o próximo valor inserido no canal.  Por omissão são acrescentados espaços à esquerda para perfazer o número de caracteres indicado.  Para usar este manipulador é necessário fazer #include <iomanip>.  Este assunto será visto em maior pormenor no Capítulo 7.

5.3.5  Matrizes como parâmetros de funções

É possível usar matrizes como parâmetros de funções.  O programa para o cálculo da média poderia ser modularizado de modo a usar funções e procedimentos do seguinte modo:
#include <iostream>

using namespace std;

const int número_de_valores = 1000;

// Preenche a matriz com valores lidos do teclado:
void lêMatriz(double m[número_de_valores])
{
    for(int i = 0; i != número_de_valores; ++i)
        cin >> m[i]; // lê o i-ésimo elemento do teclado.
}

// Devolve a média dos valores na matriz:
double médiaDaMatriz(const double m[número_de_valores])
{
    double soma = 0.0;
    for(int i = 0; i != número_de_valores; ++i)
        soma += m[i]; // acrescenta o i-ésimo elemento à soma.
    return soma / número_de_valores;
}

// Divide todos os elementos da matriz por divisor:
void normalizaMatriz(double m[número_de_valores], const double divisor)
{
    for(int i = 0; i != número_de_valores; ++i)
        m[i] /= divisor; // divide o i-ésimo elemento.
}

// Escreve todos os valores no ecrã:
void escreveMatriz(const double m[número_de_valores])
{
    for(int i = 0; i != número_de_valores; ++i)
        cout << m[i] << ' '; // escreve o i-ésimo elemento.
}

int main()
{
    // Leitura:
    cout << "Introduza " << número_de_valores << " valores: ";
    double valores[número_de_valores]; // definição da matriz com número_de_valores
                                       // elementos do tipo double.
    lêMatriz(valores);

    // Cálculo da média:
    const double média = médiaDaMatriz(valores);

    // Divisão pela média:
    normalizaMatriz(valores, média);

    // Escrita do resultado:
    escreveMatriz(valores);
    cout << endl;
}

Passagens por referência

Para o leitor mais atento o programa acima tem, aparentemente, um erro.  É que, nos procedimentos onde se alteram os valores da matriz (nomeadamente lêMatriz() e normalizaMatriz()), a matriz parece ser passada por valor e não por referência, visto que não existe na declaração dos parâmetros qualquer & (ver Passagem de argumentos por valor e por referência).  O que acontece é que o C++ passa todas as matrizes por referência e o & é, portanto, redundante *.  Assim, os dois procedimentos referidos alteram de facto a matriz que lhes é passada como argumento.

Esta é uma característica desagradável do C++, porque introduz uma excepção à semântica das chamadas de funções e procedimentos.  Esta característica mantém-se porque o C++ pretende manter compatibilidade com versões antigas da linguagem, que a herdaram do C.

* Mas poder-se-ia ter explicitado a referência escrevendo void lêMatriz(double (&m)[número_de_valores]) (os () são fundamentais), muito embora isso não seja recomendado, pois sugere que na ausência do & a passagem se faz por valor, o que não é verdade.

Dimensão das matrizes parâmetro

Há uma outra característica do tratamento das matrizes pelo C++ que pode causar alguma confusão.  Se um parâmetro de uma função ou procedimento for uma matriz, então a sua dimensão é simplesmente ignorada pelo compilador.  Assim, o compilador não verifica a dimensão das matrizes passadas como argumento, limitando-se a verificar o tipo dos seus elementos.  Esta característica está relacionada com o facto de o C++ não verificar a validade dos índices em operações de indexação, e com o facto de estarem proibidas a maior parte das operações sobre matrizes tratadas como um todo (ver Secção 5.3.6).  Assim, para o compilador de C++, lêMatriz(double m[número_de_valores]) e lêMatriz(double m[]) têm exactamente o mesmo significado *.

Este facto pode ser usado a favor do programador (se ele tiver cuidado), pois permite-lhe escrever procedimentos e funções que operam sobre matrizes de dimensão arbitrária, desde que a dimensão das matrizes seja também passada como argumento *.  Assim, na versão do programa que se segue todas as funções e procedimentos são razoavelmente genéricos, pois podem trabalhar com matrizes de dimensão arbitrária:

#include <iostream>

using namespace std;

// Preenche a matriz com n valores lidos do teclado:
void lêMatriz(double m[], const int n)
{
    for(int i = 0; i != n; ++i)
        cin >> m[i]; // lê o i-ésimo elemento do teclado.
}

// Devolve a média dos n valores na matriz:
double médiaDaMatriz(const double m[], const int n)
{
    double soma = 0.0;
    for(int i = 0; i != n; ++i)
        soma += m[i];        // acrescenta o i-ésimo elemento à soma.
    return soma / n;
}

// Divide todos os n valores da matriz por divisor:
void normalizaMatriz(double m[n], const int n, const double divisor)
{
    for(int i = 0; i != n; ++i)
        m[i] /= divisor;     // divide o i-ésimo elemento.
}

// Escreve todos os  n valores da matriz no ecrã:
void escreveMatriz(const double m[n], const int n)
{
    for(int i = 0; i != n; ++i)
        cout << m[i] << ' '; // escreve o i-ésimo elemento.
}

int main()
{
    const int número_de_valores = 1000;

    // Leitura:
    cout << "Introduza " << número_de_valores << " valores: ";
    double valores[número_de_valores]; // definição da matriz com número_de_valores
                                       // elementos do tipo double.
    lêMatriz(valores, número_de_valores);

    // Cálculo da média:
    const double média = médiaDaMatriz(valores, número_de_valores);

    // Divisão pela média:
    normalizaMatriz(valores, número_de_valores, média);

    // Escrita do resultado:
    escreveMatriz(valores, número_de_valores);
}

* Note-se que esta equivalência se deve ao compilador ignorar a dimensão de uma matriz indicada como parâmetro de uma função ou procedimento.  Isto não acontece se a passagem por referência for explicitada conforme indicado em nota anterior: nesse caso a dimensão não é ignorada e o compilador verifica se o argumento respectivo tem tipo e dimensão compatíveis.
* Na realidade o valor passado como argumento não precisa de ser o tamanho real da matriz: basta que seja menor ou igual ao tamanho real da matriz.  Isto permite processar apenas parte de uma matriz.
O caso das matrizes multidimensionais
É de notar que a linguagem C++ ignora apenas a primeira dimensão das matrizes multidimensionais definidas como parâmetros de funções ou procedimentos.  Assim, é impossível escrever
double determinante(const double m[][], const int linhas, const int colunas)
{
    ...
}
com a esperança de definir uma função para calcular o determinante de uma matriz bidimensional de dimensões arbitrárias...  É obrigatório indicar as dimensões de todas as matrizes excepto a mais "exterior":
double determinante(double m[][10], int linhas)
{
    ...
}
Ou seja, a flexibilidade neste caso resume-se a que a função pode trabalhar com um número arbitrário de linhas *.

* Na realidade nem isso, porque o determinante de uma matriz só está definido para matrizes quadradas...

5.3.6  Restrições na utilização de matrizes

Para além das incongruências e restrições já referidas relativamente à utilização de matrizes em C++, existem outras restrições que é importante conhecer.

Devolução de matrizes em funções

Não é possível devolver matrizes (directamente) em funções.  Esta restrição desagradável obriga à utilização de procedimentos para processamento de matrizes.

Operações proibidas

Também não são permitidas as atribuições ou comparações entre matrizes.  Estas operações têm de ser realizadas através da aplicação sucessiva da operação em causa a cada um dos elementos da matriz.

5.3.7  Algoritmos com matrizes

A título de exemplo desenvolvem-se nesta secção quatro algoritmos usando ciclos, em quatro funções, operando com matrizes: um para calcular a soma dos elementos de uma matriz, outro para encontrar o índice do seu maior elemento (ou de um dos seus maiores elementos), outro para verificar se os elementos de uma matriz estão todos dentro de um dado intervalo, e o último para encontrar o índice da segunda ocorrência de um dado valor numa matriz.

Soma dos elementos de uma matriz

O objectivo da função é calcular a soma dos valores dos primeiros n elementos de uma matriz m.  O primeiro passo consiste em escrever a estrutura da função.  Como é necessário no final devolver a soma dos elementos, define-se logo uma variável soma para guardar o seu valor.  Usa-se uma variável com o mesmo nome da função para que a CO do ciclo e a CO da função sejam idênticas:
int soma(const int m[], const int n)
{
    int soma = ??;
    // Aqui ficará o algoritmo propriamente dito.
    return soma;
}
O passo seguinte é a determinação da PC e da CO.  Este passo é fundamental, pois consiste em especificar o problema sem quaisquer ambiguidades.  Neste caso as condições são ambas simples, pelo que se apresentam sem comentários *
// PC: n >= 0
// CO: soma = (S j : 0 <= j < n : m[j])
int soma(const int m[], const int n)
{
    int soma = ??;
    ...
    return soma;
}
O passo seguinte consiste em, tendo-se percebido que a solução pode passar pela utilização de um ciclo, determinar uma condição invariante CI apropriada por enfraquecimento da CO.  Neste caso pode-se simplesmente substituir o limite superior do somatório (a constante n) por uma variável i inteira, acrescentando uma gama de valores apropriada para a mesma.  Assim, a estrutura da função fica:
// PC: n >= 0
// CO: soma = (S j : 0 <= j < n : m[j])
int soma(const int m[], const int n)
{
    int soma = ??;
    int i = ??;

    // CI: soma = (S j : 0 <= j < i : m[j]) e 0 <= i <= n
    while(G) {
        passo
    }
    return soma;
}

Identificada a CI, é necessário escolher uma guarda G tal que seja possível demonstrar que CI e ¬GimplicaCO.  Ou seja, escolher uma G que, quando o ciclo terminar, conduza à CO*.  Neste caso é evidente que a escolha correcta para ¬G é i = n, ou seja, G: i <> n.  Logo:
// PC: n >= 0
// CO: soma = (S j : 0 <= j < n : m[j])
int soma(const int m[], const int n)
{
    int soma = ??;
    int i = ??;

    // CI: soma = (S j : 0 <= j < i : m[j]) e 0 <= i <= n
    while(i != n) {
        passo
    }
    return soma;
}

De seguida deve-se garantir, por escolha apropriada das instruções de inicialização inic, que a CI é verdadeira no início do ciclo.  Como sempre, devem-se escolher as instruções mais simples que conduzem à veracidade de CI.  Neste caso é fácil verificar que se deve inicializar i com zero e soma também com zero (recorde-se de que a soma de zero elementos é, por definição, zero).  Ou seja:
// PC: n >= 0
// CO: soma = (S j : 0 <= j < n : m[j])
int soma(const int m[], const int n)
{
    int soma = 0;
    int i = 0;

    // CI: soma = (S j : 0 <= j < i : m[j]) e 0 <= i <= n
    while(i != n) {
        passo
    }
    return soma;
}

Como se pretende que o algoritmo termine, deve-se agora escolher um progresso que o garanta (o passo é normalmente dividido em duas partes, o progresso prog e a acção acção).  Sendo i inicialmente zero, e sendo n >= 0 (pela PC), é evidente que uma simples incrementação da variável i conduzirá à falsidade da G, e portanto à terminação do ciclo, ao fim de exactamente n iterações do ciclo:
// PC: n >= 0
// CO: soma = (S j : 0 <= j < n : m[j])
int soma(const int m[], const int n)
{
    int soma = 0;
    int i = 0;

    // CI: soma = (S j : 0 <= j < i : m[j]) e 0 <= i <= n
    while(i != n) {
        acção
        ++i;
    }
    return soma;
}

Finalmente, é necessário construir uma acção que garanta a veracidade da CI depois do passo, apesar do progresso entretanto realizado.  Sabe-se que CI e G são verdadeiras antes do passo, logo, é necessário encontrar uma acção tal que:
// CI e G: soma = (S j : 0 <= j < i : m[j]) e 0 <= i <= n e i <> n, ou seja,
// soma = (S j : 0 <= j < i : m[j]) e 0 <= i < n.
acção
++i; // o mesmo que i = i + 1;
// implica CI: soma = (S j : 0 <= j < i : m[j]) e 0 <= i <= n.
De seguida verifica-se qual a pré-condição mais fraca do progresso que garante que a CI é recuperada:
// soma = (S j : 0 <= j < i + 1 : m[j]) e 0 <= i + 1 <= n, ou seja,
// soma = (S j : 0 <= j < i + 1 : m[j]) e -1 <= i < n.
++i; // o mesmo que i = i + 1;
// CI: soma = (S j : 0 <= j < i : m[j]) e 0 <= i <= n.
Note-se que, se i >= 0, então o último termo do somatório pode ser extraído:
// soma = (S j : 0 <= j < i : m[j]) + m[i] e 0 <= i < n
// implica soma = (Sj : 0 <= j < i + 1 : m[j]) e -1 <= i < n.
++i; // o mesmo que i = i + 1;
// CI: soma = (S j : 0 <= j < i : m[j]) e 0 <= i <= n.
Conclui-se que a acção deverá ser escolhida de modo a que:
// soma = (S j : 0 <= j < i : m[j]) e 0 <= i < n.
acção
// implica soma = (Sj : 0 <= j < i : m[j]) + m[i] e 0 <= i < n.
o que se consegue facilmente com a acção:
soma += m[i];
A função completa é então:
// PC: n >= 0
// CO: soma = (S j : 0 <= j < n : m[j])
int soma(const int m[], const int n)
{
    int soma = 0;
    int i = 0;

    // CI: soma = (S j : 0 <= j < i : m[j]) e 0 <= i <= n
    while(i != n) {
        soma += m[i];
        ++i;
    }
    return soma;
}

Pode-se ainda converter o ciclo de modo a usar a instrução for:
// PC: n >= 0
// CO: soma = (S j : 0 <= j < n : m[j])
int soma(const int m[], const int n)
{
    // CI: soma = (S j : 0 <= j < i : m[j]) e 0 <= i <= n
    int soma = 0;
    for(int i = 0; i != n; ++i)
        soma += m[i];
    return soma;
}
Note-se que se manteve CI como um comentário antes do ciclo, pois é muito importante para a sua compreensão (embora, neste caso particular, por tão simples, talvez se pudesse eliminá-lo).  A CI no fundo reflecte o como o ciclo, e a função, funcionam, ao contrário da PC e da CO, que se referem àquilo que o ciclo, ou a função, faz.  A PC e a CO são úteis para o programador utilizador da função, enquanto a CI é útil para o programador fabricante e para o programador "assistência técnica", que pode precisar de verificar a correcta implementação do ciclo.

Note-se que o ciclo desenvolvido corresponde a parte da função médiaDaMatriz() usada em exemplos anteriores.

* Em todo o rigor a PC deveria indicar claramente que n é inferior ou igual à dimensão da matriz.  Para não sobrecarregar a notação assume-se que tal se verifica de aqui em diante.
* Não esquecer que CI será válida, por construção, no início, durante, e no final do ciclo (por isso se chama condição invariante), e que, quando o ciclo termina, tem de se ter forçosamente que a G é falsa, ou seja, que ¬G é verdadeira.

Índice do maior elemento de uma matriz

O objectivo é construir uma função que devolva um dos índices do máximo valor contido nos primeiros  n elementos de uma matriz m.  Como não se especifica qual dos índices devolver caso existam vários elementos com o valor máximo, arbitra-se que a função deve devolver o primeiro desses índices.  Assim, a estrutura da função é:
// PC: n > 0
// CO: 0 <= índiceDoMáximo < n e (Q j : 0 <= j < n : m[j] <= m[índiceDoMáximo]) e
//    (Q j : 0 <= j < índiceDoMáximo : m[j] < m[índiceDoMáximo])
int índiceDoMáximo(const int m[], const int n)
{
    ...
}
Ou seja, o índice devolvido tem de pertencer à gama de índices válidos para a matriz, o valor de m no índice devolvido tem de ser maior ou igual aos valores de todos os elementos da matriz (estas condições garantem que o índice devolvido é um dos índices do valor máximo na matriz) e os valores dos elementos com índice menor do que o índice devolvido têm de ser estritamente menores que o valor da matriz no índice devolvido (ou seja, o índice devolvido é o primeiro dos índices dos elementos com valor máximo na matriz).  Note-se que a PC, neste caso, impõe que n não pode ser zero, pois não tem sentido falar do máximo de um conjunto vazio.

É evidente que a procura do primeiro máximo de uma matriz pode recorrer a um ciclo.  A estrutura do ciclo é pois:

int índice = ??;
inic
while(G) {
    passo
}
// CO: 0 <= índice < n e (Q j : 0 <= j < n : m[j] <= m[índice]) e
//    (Q j : 0 <= j < índice: m[j] < m[índice])
onde a CO do ciclo se refere à variável índice, a ser devolvida pela função no seu final.

Os dois primeiros passos da construção de um ciclo, obtenção da CI e da G, neste caso, são idênticos aos do exemplo anterior (substituição da constante n por uma nova variável i):

int índice = ??;
int i = ??;
// CI: 0 <= índice < i e (Q j : 0 <= j < i : m[j] <= m[índice]) e
//    (Q j : 0 <= j < índice: m[j] < m[índice]) e 0 <= i <= n
while(i != n) {
    passo
}
// CO: 0 <= índice < n e (Q j : 0 <= j < n : m[j] <= m[índice]) e
//    (Q j : 0 <= j < índice: m[j] < m[índice])
Ou seja, a variável índice contém sempre o índice do primeiro elemento cujo valor é o máximo dos valores contidos nos i primeiros elementos da matriz.

A inicialização a usar também é simples, embora desta vez não se possa inicializar i com 0, pois nesse caso não se poderia atribuir qualquer valor a índice!   Assim, a solução é inicializar i com 1 e índice com 0.  Analisando os termos da CI um a um, verifica-se que:

  1. 0 <= índice < i: é verdadeira.
  2. (Q j : 0 <= j < i : m[j] <= m[índice]): como j só pode tomar o valor 0, é também verdadeira.
  3. (Q j : 0 <= j < índice : m[j] < m[índice]): como j não pode tomar qualquer valor, o quantificador tem, por definição, o valor verdadeiro.
  4. 0 <= i <= n: é verdadeira porque a PC obriga n a ser maior que 0.
Esta inicialização é necessária porque não existe máximo de um conjunto vazio, pelo que é necessário inicializar i com 1 e não com 0.  O ciclo fica pois:
int índice = 0;
int i = 1;
// CI: 0 <= índice < i e (Q j : 0 <= j < i : m[j] <= m[índice]) e
//    (Q j : 0 <= j < índice: m[j] < m[índice]) e 0 <= i <= n
while(i != n) {
    passo
}
// CO: 0 <= índice < n e (Q j : 0 <= j < n : m[j] <= m[índice]) e
//    (Q j : 0 <= j < índice: m[j] < m[índice])
O passo seguinte é a determinação do progresso.  Mais uma vez usa-se a simples incrementação de i em cada passo, que conduz forçosamente à terminação do ciclo.  Ou seja:
int índice = 0;
int i = 1;
// CI: 0 <= índice < i e (Q j : 0 <= j < i : m[j] <= m[índice]) e
//    (Q j : 0 <= j < índice: m[j] < m[índice]) e 0 <= i <= n
while(i != n) {
    acção
    ++i;
}
// CO: 0 <= índice < n e (Q j : 0 <= j < n : m[j] <= m[índice]) e
//    (Q j : 0 <= j < índice: m[j] < m[índice])


A parte mais interessante deste exemplo é a que falta: que acção se deve utilizar para manter a condição invariante verdadeira apesar do progresso?  A acção tem de ser tal que:

// CI e G: 0 <= índice < i e (Q j : 0 <= j < i : m[j] <= m[índice]) e
//       (Qj : 0 <= j < índice: m[j] < m[índice]) e 0 <= i <= ne i <> n, ou seja,
// 0 <= índice < ie (Q j : 0 <= j < n : m[j] <= m[índice]) e
// (Q j : 0 <= j < índice: m[j] < m[índice]) e 0 <= i < n.
acção
++i;
// implica CI: 0 <= índice < i e (Q j : 0 <= j < i : m[j] <= m[índice]) e
//        (Qj : 0 <= j < índice: m[j] < m[índice]) e 0 <= i <= n.
Mais uma vez começa-se por encontrar a pré-condição mais fraca do progresso:
// 0 <= índice < i + 1 e (Q j : 0 <= j < i + 1 : m[j] <= m[índice]) e
//    (Q j : 0 <= j < índice: m[j] < m[índice]) e 0 <= i + 1 <= n, ou seja,
// 0 <= índice <= ie (Q j : 0 <= j < i +1 : m[j] <= m[índice]) e
//    (Q j : 0 <= j < índice: m[j] < m[índice]) e -1 <= i < n.
++i; // o mesmo que i = i + 1;
// CI: 0 <= índice < i e (Q j : 0 <= j < i : m[j] <= m[índice]) e
//    (Q j : 0 <= j < índice: m[j] < m[índice]) e 0 <= i <= n.
Note-se que, se i >= 0, então o último termo do primeiro quantificador universal pode ser extraído:
0 <= índice <= i e (Qj : 0 <= j < i : m[j] <= m[índice]) em[i] <= m[índice] e
   (Q j : 0 <= j < índice: m[j] < m[índice]) e 0 <= i < n.
implica 0 <= índice <= i e (Q j : 0 <= j < i +1 : m[j] <= m[índice]) e
      (Q j : 0 <= j < índice: m[j] < m[índice]) e -1 <= i < n.
Conclui-se que a acção deverá ser escolhida de modo a que:
// 0 <= índice < ie (Q j : 0 <= j < i : m[j] <= m[índice]) e
// (Q j : 0 <= j < índice: m[j] < m[índice]) e 0 <= i < n.
acção
// implica 0 <= índice <= i e (Q j : 0 <= j < i : m[j] <= m[índice]) em[i] <= m[índice] e
//       (Qj : 0 <= j < índice: m[j] < m[índice]) e 0 <= i < n.
É claro que a acção deverá afectar apenas a variável índice, pois a variável i é afectada pelo progresso.  Mas como?  Haverá alguma circunstância em que não seja necessária qualquer alteração da variável índice, ou seja, em que a acção possa ser a instrução nula?  Comparando termo a termo as asserções antes e depois da acção, conclui-se que isso só acontece se m[i] <= m[índice].  Mas então a acção deve consistir numa instrução de selecção!  Ou seja:
// 0 <= índice < ie (Q j : 0 <= j < i : m[j] <= m[índice]) e
// (Q j : 0 <= j < índice: m[j] < m[índice]) e 0 <= i < n.
if(m[i] <= m[índice])
    // G1: m[i] <= m[índice]
    ; // instrução nula.
else
    // G2: m[i] > m[índice]
    instrução2
// implica 0 <= índice <= i e (Q j : 0 <= j < i : m[j] <= m[índice]) em[i] <= m[índice] e
//       (Qj : 0 <= j < índice: m[j] < m[índice]) e 0 <= i < n.
Resta saber que instrução deve ser usada para resolver o problema no caso em que m[i] > m[índice].  Falta, pois, falta determinar uma instrução2 tal que:
// 0 <= índice < ie (Q j : 0 <= j < i : m[j] <= m[índice]) e
// (Q j : 0 <= j < índice: m[j] < m[índice]) e 0 <= i < nem[i] > m[índice]
instrução2
// implica 0 <= índice <= i e (Q j : 0 <= j < i : m[j] <= m[índice]) em[i] <= m[índice] e
//       (Qj : 0 <= j < índice: m[j] < m[índice]) e -1 <= i < n.
Antes da instrução, índice contém o índice do primeiro elemento contendo o maior dos valores de entre os elementos com índices entre 0 e i exclusive.  Por outro lado, o elemento de índice i contém um valor superior ao valor do elemento de índice índice.  Logo, há um elemento entre 0 e i inclusive com um valor superior a todos os outros: o elemento de índice i.  Assim, a variável índice deverá tomar o valor i, de modo a continuar a ser o índice do maior do elemento com o maior dos valores inspeccionados, sendo portanto a instrução a usar:
índice = i;
A ideia é que, quando se atinge um elemento com valor maior do que aquele que se julgava até então ser o máximo, deve-se actualizar o índice do máximo.

Para verificar que assim é, calcule-se a pré-condição mais fraca que conduz à asserção final pretendida:

// 0 <= i <= ie (Q j : 0 <= j < i : m[j] <= m[i]) e m[i] <= m[i] e (Q j : 0 <= j < i: m[j] < m[i]) e 0 <= i < n, ou
// seja, (Q j : 0 <= j < i: m[j] < m[i]) e 0 <= i < n.
índice = i;
// implica 0 <= índice <= i e (Q j : 0 <= j < i : m[j] <= m[índice]) em[i] <= m[índice] e
//       (Qj : 0 <= j < índice: m[j] < m[índice]) e 0 <= i < n.
Como (riscados os termos que não são necessários para verificar a implicação)
0 <= índice < ie (Q j : 0 <= j < i : m[j] <= m[índice]) e
(Q j : 0 <= j < índice: m[j] < m[índice])e 0 <= i < n e m[i] > m[índice]
implica (Q j : 0 <= j < i: m[j] < m[i]) e 0 <= i < n,
é evidente que a atribuição resolve o problema.  Assim, a acção do ciclo é a instrução de selecção
if(m[i] <= m[índice])
    // G1: m[i] <= m[índice]
    ; // instrução nula.
else
    // G2: m[i] > m[índice]
    índice = i;
que pode ser simplificada para uma instrução condicional mais simples
if(m[i] > m[índice])
    índice = i;
O ciclo completo fica então:
int índice = 0;
int i = 1;
// CI: 0 <= índice < i e (Q j : 0 <= j < i : m[j] <= m[índice]) e
//    (Q j : 0 <= j < índice: m[j] < m[índice]) e 0 <= i <= n
while(i != n) {
    if(m[i] > m[índice])
        índice = i;
    ++i;
}
// CO: 0 <= índice < n e (Q j : 0 <= j < n : m[j] <= m[índice]) e
//    (Q j : 0 <= j < índice: m[j] < m[índice])
que pode ser convertido para um ciclo for:
int índice = 0;
// CI: 0 <= índice < i e (Q j : 0 <= j < i : m[j] <= m[índice]) e
//    (Q j : 0 <= j < índice: m[j] < m[índice]) e 0 <= i <= n
for(int i = 1; i != n; ++i)
    if(m[i] > m[índice])
        índice = i;
// CO: 0 <= índice < n e (Q j : 0 <= j < n : m[j] <= m[índice]) e
//    (Q j : 0 <= j < índice: m[j] < m[índice])
A função completa é:
// PC: n > 0
// CO: 0 <= índiceDoMáximo < n e (Q j : 0 <= j < n : m[j] <= m[índiceDoMáximo]) e
//    (Q j : 0 <= j < índiceDoMáximo : m[j] < m[índiceDoMáximo])
int índiceDoMáximo(const int m[], const int n)
{
    int índice = 0;
    // CI: 0 <= índice < i e (Q j : 0 <= j < i : m[j] <= m[índice]) e
    //    (Qj : 0 <= j < índice: m[j] < m[índice]) e 0 <= i <= n
    for(int i = 1; i != n; ++i)
        if(m[i] > m[índice])
            índice = i;
    return índice;
}

Elementos de uma matriz num intervalo

Pretende-se escrever uma função que devolva o valor lógico verdadeiro se e só se os valores dos n primeiros elementos de uma matriz m estiverem entre mínimo e máximo (inclusive).  Neste caso a estrutura da função, a PC e a CO são mais fáceis de escrever:
// PC: n >= 0
// CO: dentro = (Q j : 0 <= j < n : mínimo <= m[j] em[j] <= máximo)
bool dentro(const int m[], const int n, const int mínimo, const int máximo)
{
    ...
}
Uma vez que esta função devolve um valor booleano, que apenas pode ser V ou F, vale a pena verificar em que circunstâncias cada uma das instruções de retorno
return false;
return true;
resolve o problema.  Começa por se verificar a pré-condição mais fraca da primeira destas instruções:
// F = (Q j : 0 <= j < n : mínimo <= m[j] em[j] <= máximo), ou seja,
// (E j : 0 <= j < n : mínimo > m[j] ou m[j] > máximo).
return false;
// CO: dentro = (Q j : 0 <= j < n : mínimo <= m[j] em[j] <= máximo)
Ou seja, deve-se devolver F se existir um elemento da matriz fora da gama pretendida.

Depois verifica-se a pré-condição mais fraca da segunda das instruções de retorno:

// V = (Q j : 0 <= j < n : mínimo <= m[j] em[j] <= máximo), ou seja,
// (Q j : 0 <= j < n : mínimo <= m[j] e m[j] <= máximo).
return true;
// CO: dentro = (Q j : 0 <= j < n : mínimo <= m[j] em[j] <= máximo)
Ou seja, deve-se devolver V se todos os elementos da matriz estiverem na gama pretendida.

Que ciclo resolve o problema?  Onde colocar, se é que é possível, estas instruções de retorno?  Seja a condição invariante do ciclo:

CI: (Q j : 0 <= j < i : mínimo <= m[j] e m[j] <= máximo) e 0 <= i <= n.
onde i é uma variável introduzida para o efeito.  Esta CI afirma que todos os elementos inspeccionados até ao momento (com índices inferiores a i) estão na gama pretendida.  Note-se que esta CI foi obtida intuitivamente, e não através da metodologia de Dijkstra.  Em particular, esta CI obriga o ciclo a terminar duma forma não usual se se encontrar um elemento fora da gama pretendida, como se verá mais abaixo.

Se a guarda for

G: i <> n,
então no final do ciclo tem-se CI e ¬G, ou seja
CI e ¬G: (Q j : 0 <= j< i : mínimo <= m[j] em[j] <= máximo) e 0 <= i <= nei = n,
que implica
(Q j : 0 <= j < n : mínimo <= m[j] e m[j] <= máximo).
Logo, a instrução
return true;
deve terminar a função.

Que inicialização usar?  A forma mais simples de tornar verdadeira a CI é inicializar i com 0, pois o quantificador "qualquer que seja" sem qualquer termo tem valor lógico V.  Pode-se agora acrescentar à função o ciclo parcialmente desenvolvido:

// PC: n >= 0
// CO: dentro = (Q j : 0 <= j < n : mínimo <= m[j] em[j] <= máximo)
bool dentro(const int m[], const int n, const int mínimo, const int máximo)
{
    int i = 0;
    // CI: (Q j : 0 <= j < i : mínimo <= m[j] em[j] <= máximo) e 0 <= i <= n
    while(i != n) {
        // CIeG: (Q j : 0 <= j < i : mínimo <= m[j] e m[j] <= máximo) e 0 <= i <= ne i <> n, ou seja,
        // (Qj : 0 <= j < i : mínimo <= m[j] em[j] <= máximo) e 0 <= i < n.
        passo
    }
    return true;
}
Que progresso usar?  Pelas razões habituais, o progresso mais simples a usar é:
++i;
Resta determinar a acção de modo a que a CI seja de facto invariante.  Ou seja, é necessário garantir que
// CI e G: (Qj : 0 <= j < i : mínimo <= m[j] em[j] <= máximo) e 0 <= i < n.
acção
++i;
// implica CI: (Q j : 0 <= j < i : mínimo <= m[j] em[j] <= máximo) e 0 <= i <= n.
Verificando qual a pré-condição mais fraca que, depois do progresso, conduz à veracidade da CI, conclui-se:
// (Q j : 0 <= j < i + 1 : mínimo <= m[j] em[j] <= máximo) e 0 <= i + 1 <= n, ou seja,
// (Q j : 0 <= j < i + 1 : mínimo <= m[j] em[j] <= máximo) e -1 <= i < n.
++i; // o mesmo que i = i + 1;
// CI: (Q j : 0 <= j < i : mínimo <= m[j] em[j] <= máximo) e 0 <= i <= n.
Note-se que, se i >= 0, então o último termo do quantificador universal pode ser extraído:
// (Q j : 0 <= j < i : mínimo <= m[j] em[j] <= máximo) emínimo <= m[i] em[i] <= máximo e 0 <= i < n.
// implica (Q j : 0 <= j < i + 1 : mínimo <= m[j] em[j] <= máximo) e -1 <= i < n.
++i; // o mesmo que i = i + 1;
// CI: (Q j : 0 <= j < i : mínimo <= m[j] em[j] <= máximo) e 0 <= i <= n.
Conclui-se facilmente que, se mínimo <= m[i] em[i] <= máximo, então não é necessária qualquer acção para que a CI se verifique depois do progresso.  Isso significa que a acção consiste numa instrução de selecção:
// CI e G: (Qj : 0 <= j < i : mínimo <= m[j] em[j] <= máximo) e 0 <= i < n.
if(mínimo <= m[i] && m[i] <= máximo)
    // G1: mínimo <= m[i] e m[i] <= máximo
    ;
else
    // G2: mínimo > m[i] ou m[i] > máximo
    instrução2
++i;
// implica CI: (Q j : 0 <= j < i : mínimo <= m[j] em[j] <= máximo) e 0 <= i <= n.
Resta pois verificar que instrução deve ser usada na alternativa da instrução de selecção.  Para isso começa por se verificar que, antes dessa instrução, se verificam simultaneamente CI e G e G2, ou seja,
CI e G e G2: (Q j : 0 <= j < i : mínimo <= m[j] e m[j] <= máximo) e 0 <= i <= n e i <> n
          e (mínimo > m[i] ou m[i] > máximo)
que é o mesmo que,
CI e G e G2: (Q j : 0 <= j < i : mínimo <= m[j] e m[j] <= máximo) e 0 <= i < n
          e (mínimo > m[i] ou m[i] > máximo)
Traduzindo para português vernáculo: "os primeiros i elementos da matriz estão dentro da gama pretendida mas o i+1-ésimo (de índice i) não está".  É claro portanto que
CI e G e G2 implica (E j : 0 <= j < i + 1 : mínimo > m[j] ou m[j] > máximo) e 0 <= i < n
         implica (E j : 0 <= j < n : mínimo > m[j] ou m[j] > máximo)
Ou seja, existe pelo menos um elemento com índice entre 0 e i inclusive que não está na gama pretendida e portanto o mesmo se passa para os elementos com índices entre 0 e n exclusive.

Logo, a instrução alternativa da instrução de selecção deve ser return false;, pois termina imediatamente a função (e portanto o ciclo), devolvendo o valor apropriado (ver pré-condição mais fraca desta instrução mais atrás).

Assim, a função fica:

// PC: n >= 0
// CO: dentro = (Q j : 0 <= j < n : mínimo <= m[j] em[j] <= máximo)
bool dentro(const int m[], const int n, const int mínimo, const int máximo)
{
    int i = 0;
    // CI: (Q j : 0 <= j < i : mínimo <= m[j] em[j] <= máximo) e 0 <= i <= n
    while(i != n) {
        if(mínimo <= m[i] && m[i] <= máximo)
            // G1: mínimo <= m[j] em[j] <= máximo
            ;
        else
        // G2: mínimo > m[j] ou m[j] > máximo
            return false;
        ++i;
    }
    return true;
}
Ou, trocando as instruções controladas pela instrução de selecção (e convertendo-a numa instrução condicional) e convertendo o ciclo while num ciclo for:
// PC: n >= 0
// CO: dentro = (Q j : 0 <= j < n : mínimo <= m[j] em[j] <= máximo)
bool dentro(const int m[], const int n, const int mínimo, const int máximo)
{
    // CI: (Q j : 0 <= j < i : mínimo <= m[j] em[j] <= máximo) e 0 <= i <= n
    for(int i = 0; i != n; ++i)
        if(mínimo > m[i] || m[i] > máximo)
            return false;
    return true;
}

Segundo elemento de uma matriz com um dado valor

O objectivo agora é encontrar o índice do segundo elemento com valor k numa matriz m com n elementos.  Neste caso a PC é um pouco mais complicada do que para os exemplos anteriores, pois tem de se garantir que existem pelo menos dois elementos com o valor pretendido, o que, por si só, implica que a matriz tem de ter pelo menos dois elementos.  A CO é mais simples.  Diz que o índice a devolver deve corresponder a um elemento com valor k e que no conjunto dos elementos com índice menor existe apenas um elemento com valor k (diz ainda que o índice deve ser válido, neste caso maior do que 0, porque têm de existir pelo menos dois elementos com valores iguais até ao índice).  Assim, a estrutura da função é:
// PC: n >= 2 e (N j : 0 <= j < n : m[j] = k) >= 2
// CO: (N j : 0 <= j < índiceDoSegundo : m[j] = k) = 1 e m[índiceDoSegundo] = k
//    e 0 < índiceDoSegundo < n
int índiceDoSegundo(const int m[], const int n, const int k)
{
    ...
}
Para resolver este problema é necessário um ciclo, que pode ter a seguinte estrutura:
// PC: n >= 2 e (N j : 0 <= j < n : m[j] = k) >= 2
int i = ??;
inic
while(G) {
    passo
}
return i;
// CO: (N j : 0 <= j < i : m[j] = k) = 1 e m[i] = k e 0 < i < n
onde a CO do ciclo se refere à variável i, a ser devolvida pela função no seu final.

Neste caso não existe na CO do ciclo um quantificador onde se possa substituir (com facilidade) uma constante por uma variável.  Assim, a determinação da CI pode ser tentada factorizando a CO, que é uma conjunção, em CI e ¬G.  Uma observação atenta das condições revela que a escolha apropriada é

CI: (N j : 0 <= j < i : m[j] = k) = 1 e  0 < i < n
¬G: m[i] = k
Que significa esta CI?  Apenas que, durante todo o ciclo, tem de se garantir que o número de elementos da matriz com índices entre 0 e i exclusive e com valor k é sempre 1.

O ciclo pode-se agora escrever como:

// PC: n >= 2 e (N j : 0 <= j < n : m[j] = k) >= 2
int i = ??;
inic
CI: (N j : 0 <= j < i : m[j] = k) = 1 e  0 < i < n
while(m[i] != k) {
    passo
}
// CO: (N j : 0 <= j < i : m[j] = k) = 1 e m[i] = k e 0 < i < n
return i;
Um problema com a escolha que se fez para a CI é que, aparentemente, não é fácil fazer a inicialização.  Em vez de atacar imediatamente esse problema, assume-se daqui em diante que a inicialização está feita (ver em E a inicialização? como se pode inicializar).  O passo seguinte, portanto, é determinar o passo do ciclo.  Antes do passo tem-se CI e G, ou seja:
CI e G: (N j : 0 <= j < i : m[j] = k) = 1 e  0 < i < n e m[i] <> k
Mas
(N j : 0 <= j < i : m[j] = k) = 1 e m[i] <> k
é o mesmo que
(N j : 0 <= j < i + 1 : m[j] = k) = 1
pois, sendo m[i] <> k, pode-se estender a gama de valores de j sem afectar a contagem de afirmações verdadeiras.  Ou seja:
CI e G: (N j : 0 <= j < i + 1 : m[j] = k) = 1 e  0 < i < n.
Atente-se bem na expressão acima.  Será que pode ser verdadeira quando i atinge o seu maior valor superior i = n - 1?  O segundo termo da conjunção é claramente verdadeiro para i = n - 1, pois n > 1 pela PC.  E o primeiro termo?  Sendo i = n - 1, o primeiro termo fica:
(N j : 0 <= j < n : m[j] = k) = 1
o que não pode acontecer, dada a PC!  Logo i <> n - 1, e portanto
CI e G: (N j : 0 <= j < i + 1 : m[j] = k) = 1 e  0 < i < n - 1.
O passo tem de ser escolhido de modo a garantir a invariância de CI, ou seja, de modo a garantir que
// CI e G: (Nj : 0 <= j < i + 1 : m[j] = k) = 1 e  0 < i < n - 1
passo
// implica CI: (N j : 0 <= j < i : m[j] = k) = 1 e  0 < i < n
Começa por se escolher um progresso apropriado.  Qual a forma mais simples de garantir que a guarda se torna falsa ao fim de um número finito de passos?  Simplesmente incrementando i.  Se i atingisse alguma vez o valor n (índice para além do fim da matriz) sem que a guarda se tivesse alguma vez tornado falsa, isso significaria que a matriz não possuía dois elementos pelo menos com o valor k, o que violaria a PC!  Logo, o ciclo tem de terminar antes de i atingir n, ao fim de um número finito de passos, portanto.  O passo do ciclo pode então ser escrito como:
// CI e G: (Nj : 0 <= j < i + 1 : m[j] = k) = 1 e  0 < i < n - 1
acção
++i;
// implica CI: (N j : 0 <= j < i : m[j] = k) = 1 e  0 < i < n
ou, determinando a pré-condição mais fraca do progresso que conduz à verificação da CI no seu final,
// CI e G: (Nj : 0 <= j < i + 1 : m[j] = k) = 1 e  0 < i < n - 1
acção
// (N j : 0 <= j < i + 1 : m[j] = k) = 1 e  0 < i + 1 < n, ou seja,
// (N j : 0 <= j < i + 1 : m[j] = k) = 1 e  -1 < i < n - 1
++i;
// implica CI: (N j : 0 <= j < i : m[j] = k) = 1 e  0 < i < n
Assim sendo, a acção terá de ser escolhida de modo a garantir que
// CI e G: (Nj : 0 <= j < i + 1 : m[j] = k) = 1 e  0 < i < n - 1
acção
// implica (N j : 0 <= j < i + 1 : m[j] = k) = 1 e  -1 < i < n - 1
Mas isso consegue-se sem necessidade de qualquer instrução, pois
0 < i < n - 1 implica -1 < i < n - 1.
Logo, o ciclo necessário é:
// PC: n >= 2 e (N j : 0 <= j < n : m[j] = k) >= 2
int i = ??;
inic
CI: (N j : 0 <= j < i : m[j] = k) = 1 e  0 < i < n
while(m[i] != k)
    ++i;
// CO: (N j : 0 <= j < i : m[j] = k) = 1 e m[i] = k e 0 < i < n
return í;
E a inicialização?
A inicialização do ciclo anterior é um problema por si só, com as mesmas pré-condições, mas com uma outra condição objectivo, igual à condição invariante do ciclo já desenvolvido.  Isto é, o problema a resolver é:
// PC: n >= 2 e (N j : 0 <= j < n : m[j] = k) >= 2
int i = ??;
inic
// CI: (N j : 0 <= j < i : m[j] = k) = 1 e  0 < i < n
Ou seja, pretende-se que i seja maior do que o índice da primeira ocorrência de k na matriz.  A solução para este problema é mais simples se se reforçar a condição objectivo um pouco mais.  Em particular, pode-se impor que i seja o índice imediatamente após a primeira ocorrência de k.  Isto é:
// PC: n >= 2 e (N j : 0 <= j < n : m[j] = k) >= 2
int i = ??;
inic
// (N j : 0 <= j < i : m[j] = k) = 1 e m[i - 1] = k e 0 < i < n
// implica CI: (N j : 0 <= j < i : m[j] = k) = 1 e  0 < i < n
ou mais simples ainda: se se terminar a inicialização com uma incrementação de i e se calcular a pré-condição mais fraca dessa incrementação:
// PC: n >= 2 e (N j : 0 <= j < n : m[j] = k) >= 2
int i = ??;
inic
// (N j : 0 <= j < i + 1 : m[j] = k) = 1 e m[i] = k e 0 < i + 1 < n, ou seja,
// (N j : 0 <= j < i + 1 : m[j] = k) = 1 e m[i] = k e 0 <= i < n - 1
++i;
// (N j : 0 <= j < i : m[j] = k) = 1 e m[i - 1] = k e 0 < i < n
// implica CI: (N j : 0 <= j < i : m[j] = k) = 1 e  0 < i < n
Note-se que, sendo 0 <= i < n - 1, então
(N j : 0 <= j < i + 1 : m[j] = k) = 1 e m[i] = k e 0 <= i < n - 1
é o mesmo que
(N j : 0 <= j < i : m[j] = k) = 0 e m[i] = k e 0 <= i < n - 1
ou ainda (ver Apêndice A)
(Q j : 0 <= j < i : m[j] <> k) e m[i] = k e 0 <= i < n - 1
pelo que o código de inicialização se pode escrever:
// PC: n >= 2 e (N j : 0 <= j < n : m[j] = k) >= 2
int i = ??;
inic
// CO': (Q j : 0 <= j < i : m[j] <> k) em[i] = k e 0 <= i < n - 1
++i;
// implica CI: (N j : 0 <= j < i : m[j] = k) = 1 e  0 < i < n
onde CO' representa a condição objectivo do código de inicialização do ciclo já desenvolvido, e não a CO do ciclo já desenvolvido ou mesmo da função.

Ou seja, a inicialização reduz-se ao problema de encontrar o índice do primeiro elemento com valor k.  Este índice é forçosamente inferior a n -1, pois a matriz, pela PC, possui dois elementos com valor k!  A solução deste problema passa pela construção de um outro ciclo e é relativamente simples, pelo que se apresenta a solução sem mais comentários (dica: factorize-se a CO'):

// PC: n >= 2 e (N j : 0 <= j < n : m[j] = k) >= 2
int i = 0;
// CI': (Q j : 0 <= j < i : m[j] <> k) e 0 <= i < n - 1
while(m[i] != k)
    ++i;
// CO': (Q j : 0 <= j < i : m[j] <> k) em[i] = k e 0 <= i < n - 1
++i;
// implica CI: (N j : 0 <= j < i : m[j] = k) = 1 e  0 < i < n
Função completa
Concluindo, a função completa é:
// PC: n >= 2 e (N j : 0 <= j < n : m[j] = k) >= 2
// CO: (N j : 0 <= j < índiceDoSegundo : m[j] = k) = 1 e m[índiceDoSegundo] = k
//    e 0 < índiceDoSegundo < n
int índiceDoSegundo(const int m[], const int n, const int k)
{
    int i = 0;
    // CI': (Qj : 0 <= j < i : m[j] <> k) e 0 <= i < n - 1
    while(m[i] != k)
        ++i;
    // CO': (Qj : 0 <= j < i : m[j] <> k) em[i] = k e 0 <= i < n - 1
    ++i;
    // CI: (N j : 0 <= j < i : m[j] = k) = 1 e  0 < i < n
    while(m[i] != k)
        ++i;
    return í;
}
Usando instruções de asserção
Note-se que o parâmetro constante n não é usado na função desenvolvida!  Será boa ideia eliminá-lo da lista de parâmetros?

Acontece que, muitas vezes, é conveniente verificar explicitamente a veracidade das PC e CO das funções ou procedimentos (e ciclos) no próprio código C++.  Dessa forma detectam-se mais facilmente erros por parte do programador utilizador dessas funções ou procedimentos, ou mesmo erros cometidos pelo programador fabricante da função ou procedimento em causa.  Isto é particularmente importante se o programa em desenvolvimento estiver a ser depurado e incluir indexação de matrizes.

Existe uma forma padronizada de explicitar as asserções, obrigando o computador a verificar a sua validade durante a execução do programa: usando as chamadas instruções de asserção.  Para a função desenvolvida, não é fácil verificar a PC sem utilizar um ciclo para contabilizar o número de ocorrências do valor k (era possível escrever uma função para esse efeito, ver mais abaixo).  Mas é possível garantir que i nunca atinge o valor de n, pois de outra forma a PC não poderia ser verdadeira.  Assim, pode-se "artilhar" a função anterior com instruções de asserção apropriadas:

// PC: n >= 2 e (N j : 0 <= j < n : m[j] = k) >= 2
// CO: (N j : 0 <= j < índiceDoSegundo : m[j] = k) = 1 e m[índiceDoSegundo] = k
//    e 0 < índiceDoSegundo < n
int índiceDoSegundo(const int m[], const int n, const int k)
{
    assert(n >= 2);
    int i = 0;
    assert(i < n);
    // CI': (Qj : 0 <= j < i : m[j] <> k) e 0 <= i < n - 1
    while(m[i] != k) {
        ++i;
        assert(i < n);
    }
    // CO': (Qj : 0 <= j < i : m[j] <> k) em[i] = k e 0 <= i < n - 1
    ++i;
    assert(i < n);
    // CI: (N j : 0 <= j < i : m[j] = k) = 1 e  0 < i < n
    while(m[i] != k) {
        ++i;
        assert(i < n);
    }
    return i;
}
As instruções de asserção consistem na palavra assert seguida de uma expressão booleana (entre parênteses) que se pretende seja verdadeira no ponto do programa em causa.  A utilização de instruções de asserção exige a inclusão do ficheiro de interface cassert (assunto a estudar mais tarde).  Suponha-se o seguinte programa de teste da função acima:
#include <iostream>
#include <cassert>

using namespace std;

// PC: n >= 2 e (Nj : 0 <= j < n : m[j] = k) >= 2
// CO: (N j : 0 <= j < índiceDoSegundo : m[j] = k) = 1 e m[índiceDoSegundo] = k
//    e 0 < índiceDoSegundo < n
int índiceDoSegundo(const int m[], const int n, const int k)
{
    assert(n >= 2);
    int i = 0;
    assert(i < n);
    // CI': (Qj : 0 <= j < i : m[j] <> k) e 0 <= i < n - 1
    while(m[i] != k) {
        ++i;
        assert(i < n);
    }
    // CO': (Qj : 0 <= j < i : m[j] <> k) em[i] = k e 0 <= i < n - 1
    ++i;
    assert(i < n);
    // CI: (N j : 0 <= j < i : m[j] = k) = 1 e  0 < i < n
    while(m[i] != k) {
        ++i;
        assert(i < n);
    }
    return i;
}

int main()
{
    const int matriz[] = {1, 2, 1, 3, 4};
    // Como se verá mais tarde, sizeof é um operador que permite saber quanta memória ocupam
    // as variáveis e tipos:
    const int n = sizeof(matriz) / sizeof(int); // fica com 5.

    int i1 = índiceDoSegundo(matriz, n, 1);
    cout << i1 << endl;

    int i2 = índiceDoSegundo(matriz, n, 3);
    cout << i2 << endl;
}

É evidente que a primeira invocação da função resultará no índice 2, mas que na segunda invocação a matriz e o valor a procurar não verificam a PC., i.e., não existem dois elementos da matriz com o valor 3.  Que sucede na prática?  Durante o segundo ciclo da função o valor 3 não é encontrado e portanto a variável i acaba por atingir o valor de n (5).  Nessa altura a instrução de asserção assert(i < n); aborta o programa com uma mensagem de erro semelhante à seguinte:
nome_do_ficheiro_executável: nome_do_ficheiro_C++:24: int índiceDoSegundo(const int *, int, int): Assertion `i < n' failed.
onde se indicam:
  1. O nome do ficheiro executável onde ocorreu o erro.
  2. O nome do ficheiro em linguagem C++ onde ocorreu o erro.
  3. O número da linha do ficheiro C++ onde ocorreu o erro.
  4. O cabeçalho da função ou procedimento onde ocorreu o erro (só em alguns compiladores).
  5. A expressão que deveria ser verdadeira mas não o era.
Alternativamente seria possível escrever uma função para contar as ocorrência de um valor numa matriz e usá-la para explicitar as asserções da função em estudo, o que tornaria o código mais claro:
#include <iostream>
#include <cassert>

using namespace std;

// PC: n >= 0
// CO: ocorrências = (Nj : 0 <= j < n : m[j] = k)
int ocorrências(const int m[], const int n, const int k)
{
    assert(n >= 0);
    int ocorrências = 0;
    // CI: ocorrências = (N j : 0 <= j < i : m[j] = k) e 0 <= i <= n
    for(int i = 0; i != n; ++i)
        if(m[i] == k)
            ++ocorrências;
    // Que instrução de asserção colocaria aqui?
    return ocorrências;
}

// PC: n >= 2 e (Nj : 0 <= j < n : m[j] = k) >= 2
// CO: (N j : 0 <= j < índiceDoSegundo : m[j] = k) = 1 e m[índiceDoSegundo] = k
//    e 0 < índiceDoSegundo < n
int índiceDoSegundo(const int m[], const int n, const int k)
{
    assert(n >= 2 && ocorrências(m, n, k) >= 2);
    int i = 0;
    // CI': (Qj : 0 <= j < i : m[j] <> k) e 0 <= i < n - 1
    while(m[i] != k)
        ++i;
    // CO': (Qj : 0 <= j < i : m[j] <> k) em[i] = k e 0 <= i < n - 1
    assert(0 <= i && i < n - 1 && m[i] == k && ocorrências(m, i, k) == 0);
    ++i;
    // CI: (N j : 0 <= j < i : m[j] = k) = 1 e  0 < i < n
    while(m[i] != k)
        ++i;
    assert(ocorrências(m, i, k) == 1 && m[i] == k && 0 < i && i < n);
    return i;
}

int main()
{
    const int matriz[] = {1, 2, 1, 3, 4};
    // Como se verá mais tarde, sizeof é um operador que permite saber quanta memória ocupam
    // as variáveis e tipos:
    const int n = sizeof(matriz) / sizeof(int); // fica com 5.

    int i1 = índiceDoSegundo(matriz, n, 1);
    cout << i1 << endl;

    int i2 = índiceDoSegundo(matriz, n, 3);
    cout << i2 << endl;
}

Neste caso o programa abortaria com uma mensagem de erro um pouco mais clara:
nome_do_ficheiro_executável: nome_do_ficheiro_C++:25: int índiceDoSegundo(const int *, int, int): Assertion `n >= 2 && ocorrências(m, n, k) >= 2' failed.
A colocação criteriosa de instruções de selecção é um mecanismo extremamente útil para a depuração de programas.  Mas tem uma desvantagem aparente: as verificações da asserções consomem tempo.  Para quê, então, continuar a fazer essas verificações quando o programa já estiver liberto de erros?  O mecanismo das instruções de asserção é interessante porque permite evitar esta desvantagem com elegância: basta definir uma macro de nome NDEBUG (no debug) para que as asserções deixem de ser verificadas e portanto deixem de consumir tempo, não sendo necessário apagá-las do código.  As macros serão explicadas num capítulo posterior, sendo suficiente para já saber que a maior parte dos compiladores para Unix (ou Linux) permitem a definição dessa macro duma forma muito simples: basta dar a opção -DNDEBUG ao compilador.

Assim sendo, é boa prática colocar asserções para verificação das PC e CO de ciclos e funções, o que auxilia durante o desenvolvimento e depuração do programa, e desactivá-las definindo a macro NDEBUG quando o programa estiver livre de erros (ou assim parecer...).

A título de exercício, sugere-se a execução do programa acima compilado sem e com a macro NDEBUG definida.

E se não existir?
Ao se desenvolver a função índiceDoSegundo() poder-se-ia ter especificado que, caso o número de ocorrências do valor k na matriz fosse inferior a 2, esta deveria devolver o valor n, pois é sempre um índice inválido (os índices válidos variam entre 0 e n - 1) sendo por isso um valor apropriado para indicar uma condição de erro.  Nesse caso a função poderia ser escrita como:
// PC: n >= 0
// CO: ((N j : 0 <= j < índiceDoSegundo : m[j] = k) = 1 e m[índiceDoSegundo] = k
//     e 0 < índiceDoSegundo < n) ou
//    ((N j : 0 <= j < n : m[j] = k) < 2 e índiceDoSegundo = n)
int índiceDoSegundo(const int m[], const int n, const int k)
{
    assert(n >= 0);
    int i = 0;
    // CI: ((Qj : 0 <= j < i : m[j] <> k) e 0 <= i <= n
    while(i != n && m[i] != k)
        ++i;
    if(i == n)
        return n;
    ++i;
    // CI: ((Nj : 0 <= j < i : m[j] = k) = 1 e 1 <= i <= n
    while(i != n && m[i] != k)
        ++i;
    return i;
}
Solução genérica
Uma solução mais genérica para o problema poderia ser desenvolvida reconhecendo que o código anterior é repetitivo:
// PC: n >= 0 eésimo > 0
// CO: ((N j : 0 <= j < índiceDoÉsimo : m[j] = k) = ésimo - 1 e m[índiceDoÉsimo] = k
//     e ésimo - 1 <= índiceDoÉsimo < n) ou
//    ((N j : 0 <= j < n : m[j] = k) < ésimoeíndiceDoÉsimo = n)
int índiceDoÉsimo(const int m[], const int n, const int k, const int ésimo)
{
    assert(n >= 0 && ésimo > 0);
    int i = -1;
    int oc = 0;  // número de ocorrências, para não se confundir com a função.
    do {
        ++i;
        // CI: (N j : 0 <= j < i : m[j] = k) = oc e oc <= i <= n
        while(i != n && m[i] != k)
            ++i;
        if(i == n) {
            assert(ocorrências(m, n, k) < ésimo);
            return n;
        }
    } while(++oc != ésimo);

    assert(ocorrências(m, i, k) == ésimo - 1 && m[i] == k &&
           ésimo - 1 <= i && i < n);
    return i;
}

5.3.8  Alternativa às matrizes

Viu-se que as matrizes em C++, de hora em diante conhecidas por "matrizes clássicas do C++", têm um conjunto de particularidades que as tornam pouco simpáticas de utilizar na prática.  No entanto, a linguagem C++ traz associada uma biblioteca padrão que disponibiliza um conjunto muito vasto de ferramentas (funções, procedimentos, variáveis, tipos, constantes, etc.), entre os quais uma classe modelo chamada vector.  Esta classe modelo é uma excelente alternativa às matrizes clássicas do C++ descritas neste capítulo e será apresentada concisamente na Secção 7.1.  No capítulo sobre programação genérica abordar-se-á as classes modelo.

5.3.9  Exercícios

1. Construa uma função ou procedimento que, dada uma matriz m de inteiros com n elementos (entre parênteses, a PC a impor):

1.a)  Inverta a ordem dos valores na matriz (n >= 0).
1.b)  Verifique se os valores dos elementos estão por ordem (não estritamente) crescente (n >= 0, pois sequências com 0 ou 1 elementos estão, por definição, por qualquer ordem que se deseje).
1.c)  Devolva o índice da primeira ocorrência de um valor k, sabendo que ele existe na matriz (logo n > 0).
1.d)  Devolva o índice da primeira ocorrência de um valor k, se o valor não existir deve devolver n (n >= 0).
1.e)  Devolva o maior valor existente na matriz (n > 0).  Pode usar alguma função já desenvolvida?
1.f)  Devolva o maior valor existente na matriz e calcule o número de vezes que ocorre (n > 0).  Use referências para guardar o número de ocorrências calculado.
1.g)  Verifique se os valores dos elementos são todos iguais (n >= 0, pois sequências com 0 ou 1 elementos são, por definição, constantes).
1.h)  Verifique se os valores dos elementos estão por ordem estritamente crescente (n >= 0, pois sequências com 0 ou 1 elementos estão, por definição, por qualquer ordem que se deseje).
1.i)  Verifique se os valores dos elementos estão por ordem crescente ou decrescente, ou seja, se a sequência de elementos é monótona (n >= 0, pois sequências com 0 ou 1 elementos são, por definição, monótonas).
1.j)  (Difícil) Devolva o índice de uma ocorrência de um valor k, sabendo que ele existe na matriz (logo n > 0) e sabendo que os valores na matriz estão por ordem crescente.  Como pode tirar partido da ordenação da matriz?
k)  (Difícil) Desloque todos os valores de m posições para a direita circularmente, i.e., se os valores saírem à direita, entram à esquerda (n > 0). Como resolver sem impor restrições a m?  Como resolver sem restrições em m e com uma única variável auxiliar?
l)  Sendo um "planalto" uma sequência contígua de valores idênticos, devolva o comprimento do planalto mais longo na matriz (n >= 0).

2.a)  Crie uma função que calcule a norma de um vector de 10 float.  Faça um pequeno programa para testar esta função.
2.b)  Crie uma função que normalize um vector de 10 float.  Normalizar consiste em dividir cada um dos componentes pela norma do vector.  Faça um pequeno programa para testar esta função.

3.  Crie uma função que calcule o produto interno de dois vectores de float.  Faça um pequeno programa para testar esta função.

4.  Crie uma função que preencha uma matriz a de 10 por 10 elementos inteiros de tal forma que o elemento ai,j da matriz tenha o valor ij.  Faça um pequeno programa para testar esta função.

5.  Escreva um procedimento que permita preencher matrizes de dimensão n × n do seguinte modo (exemplo para o caso particular de n = 4):

13 14 15 16
12  3  4  5
11  2  1  6
10  9  8  7
6.  Estude a classe modelo vector (Secção 7.1) e refaça os exercícios anteriores usando-a.

5.4  Referências

[1]  Bjarne Stroustrup, "The C++ Programming Language", terceira edição, Addison-Wesley, Reading, Massachusetts, 1998. *

* Existe na biblioteca do ISCTE.