Guião da 5ª Aula Prática

Resoluções

1.a)  Ver ex1a.C.

1.b)  A simples transferência dos procedimentos para depois da função main() leva o compilador a gerar mensagens de erro, pois necessita de conhecer o cabeçalho de uma rotina para saber como pode ser feita a sua invocação: o compilador lê o programa de cima para baixo, e por isso quando compila a função main() ainda não viu as definições dos procedimentos.  A solução passa por declarar os procedimentos, sem os definir, antes da função main().  Ver ex1b.C.

2.  Os valores constantes na tabela estão correctos.

3.a)  Funções já desenvolvidas na aula teórica, se tudo correu bem (excepto que na teórica a base era double e as funções devolviam, naturalmente, também double).  Nesse caso pôr o ênfase na determinação do traçado da função.  Ver ex3a.C.  A tabela fica:

3.b)  Ver notas em 3.a).  A utilização de expoentes negativos obriga a devolver valores decimais.  Nesse caso torna-se absurdo não aceitar também como base da potência valores decimais.  Assim, em vez de "corrigir" a função, escreveu-se uma nova versão, sobrecarregada com a primeira.  Note-se que a nova versão não admite que a base seja nula e o expoente negativo.  Ver ex3b.C.

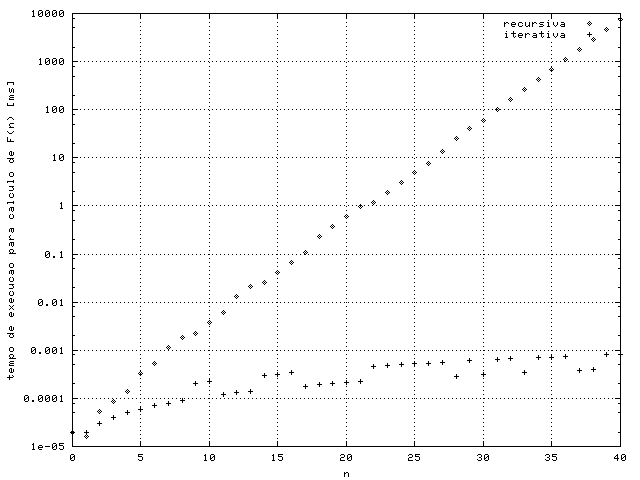
4.a) e 4.b)  Ver fib.C.  O gráfico deve dar algo parecido com:

5.  O número de invocações da função recursiva fibonacciRecursiva() quando invocada com um argumento de valor n, a que se pode chamar N_n, pode ser calculado como se segue:

1. Para n = 0 e n = 1 é claro que N_n = 1.
2. Para n > 1, uma invocação da função é seguida das chamadas da mesmas função com argumentos n - 1 e n - 2, pelo que N_n = 1 + N_n-1 + N_n-2.

N₀ = 1
N₁ = 1
N_n = 1 + N_n-1 + N_n-2, se n > 1

É fácil demonstrar que N_n = 2×F_n+1 - 1.  Como a sucessão cresce muito depressa, percebe-se a ineficiência da versão recursiva...

Ver ex5.C.  Experimente-se o programa com o valor 35.

6.a)  Ver ex6a.C.

6.b)  Ver ex6b.C.