
Escrever no quadro:
Apresentar o docente, dizer contactos.
Pedir contactos do delegado de turma.
Explicar razão de ser das aulas teóricas a turmas separadas: interacção. Explicar liberdade de frequência: se não estão interessados ou atentos, saiam ou nem cheguem a entrar. Para os convencer de que responder erradamente é normal, pedir-lhes para fazerem em coro uma qualquer palhaçada no início e depois dizer que pior que a figura de parvos que acabaram de fazer é impossível! Referir pavor do ridículo dos portugueses.
Dizer que a apresentação formal é na sala marcada pelo GARE ou na aula prática do turno A. Dizer qual é.
Começar por perguntar se sabem o que é um computador. Escrever as respostas no quadro. Discuti-las.
Um computador é uma máquina (ou utensílio ou ferramenta). Mas que um martelo ou uma máquina de lavar também são máquinas. Que distingue o computador? Ser programável. De acordo, mas a máquina de lavar também tem programas... É uma máquina programável genérica. Só com muita imaginação se pode usar uma máquina de lavar para gerir as contas num banco...
O que é programar então? É ensinar um computador a resolver determinado problema ou determinados tipos de problemas.
Escrever a frase:
Donde, se o programador ensinou o computador a resolver o problema, então o programador sabe resolvê-lo. Daí que não seja exagero classificar a programação como a Arte de Resolver Problemas.Diz-se que só se compreende realmente um assunto depois de o ter ensinado a alguém. Na realidade só se compreende realmente um assunto depois de o ter ensinado a um computador.
Knuth
Um conceito importante em programação é o de algoritmo. Um algoritmo está (quase) para a programação como uma receita para o culinária.
Fazer o quadro abaixo (escrever só a coluna da direita). Eles que adivinhem a da esquerda. Também se pode fazer ao contrário. Ou alternado.
Um computador é mais do que um simples executor de ordens. Um computador tem:
Explorar respostas.
| Programação | Culinária |
|---|---|
| Algoritmo | Receita (abstracta) |
| Programa | Receita (numa linguagem) |
| Entradas | Número de pratos |
| Saídas | Pratos |
| Valores | Ingredientes |
| Variáveis | Recipientes |
| Memória volátil (RAM) | Bancada |
| Memória permanente (discos, etc.) | Frigorífico, despensa |
| Computador | Cozinha |
| Processador | Cozinheiro |
| Comentários | Apartes para o cozinheiro |
Os algoritmos têm cinco características importantes:
Entradas: m e n (exemplo 12 e 8)
Saída: k tal que k = mdc(m, n)
Desenhar variáveis usando notação UML! Usar ? para o valor de k.
Relembrar divisão inteira. Introduzir ÷ para o resto.
m, n e k são variáveis inteiras. O que é isso? Para já podemos imaginar que são caixas, cada uma das quais contém um e um só número inteiro. Cada variável tem um nome (por exemplo, m), um tipo (por exemplo, inteiro) e um valor (por exemplo, 12).
Numa variável há duas características fixas e uma variável. O nome e o tipo são fixos. O valor é variável.
Como m e n são entradas já lá têm valores (12 e 8, neste caso):


A variável k contém o quê? Lixo! Lixo? O que é isso? É um inteiro qualquer, sobre o qual não temos qualquer controlo:

Uma analogia com a culinária diria que os recipientes estão para a culinária como as variáveis para a programação. Mas a analogia não é perfeita: as variáveis contêm sempre qualquer coisa!
É uma cozinha algo estranha, onde os recipientes têm sempre alguma coisa dentro, mesmo quando arrumados... E ainda por cima, muitas vezes é lixo...
Regras do jogo: o nosso algoritmo é uma sequência de instruções que agem sobre as variáveis existentes.
Como se resolve o problema?
Pedir aos alunos propriedades interessantes do máximo divisor comum. Anotá-las e discuti-las. Frisar:
Explicar <-. Explicar ordem de execução. Explicar enquanto: enquanto o açúcar não estiver no ponto ir mexendo.se m < n então
k <- m
senãok <- nenquanto m ÷ k <> 0 ou n ÷ k <> 0 faça-se:
k <- k - 1
Será que isto é mesmo um algoritmo? I.e., é finito, bem definido, tem entradas e saídas e cada operação é eficaz?
Que tem entradas e saídas já sabemos. Que é bem definido, não há dúvidas, pois cada passo está bem especificado. As operações são todas eficazes. Falta saber que termina sempre e com o valor correcto!
Vamos testar com os valores de entrada 12 e 8.
Fazer traçado alterando valor em k. Chamar-lhe traçado.
Funcionou! Será que funciona sempre? Podíamos testar agora com 12 e 45, por exemplo. E depois? Não se pode demonstrar que um algoritmo funciona através de testes! Quando muito demonstra-se que não funciona.
Para demonstrar que funciona teríamos de testar todos os pares de inteiros positivos, que infelizmente são infinitos. Porquê testar com todos? Porque nada nos garante que se o algoritmo produzir resultados correctos para os primeiros 1000 pares, os produzirá também para todos os restantes pares.
Suponham que só nos interessam inteiros até um milhão. Se demorarmos 1 milionésimo de segundo a testar cada par, ainda demoramos 1000000 de segundos, ou seja, 12 dias...
Como demonstrá-lo, então?
O ideal é fazer esta explicação num diagrama de actividade, colocando as asserções como comentários. Ver folhas teóricas. Usar a nomenclatura indicada na primeira figura:
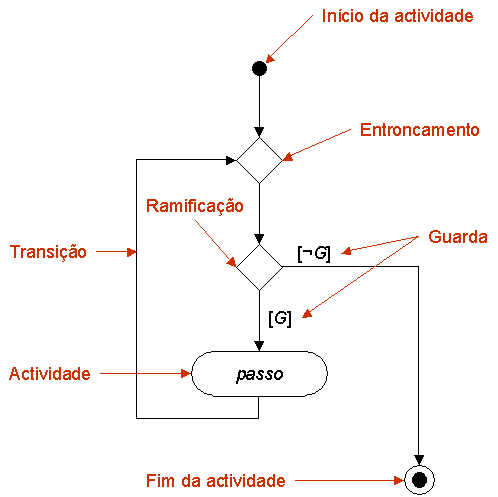
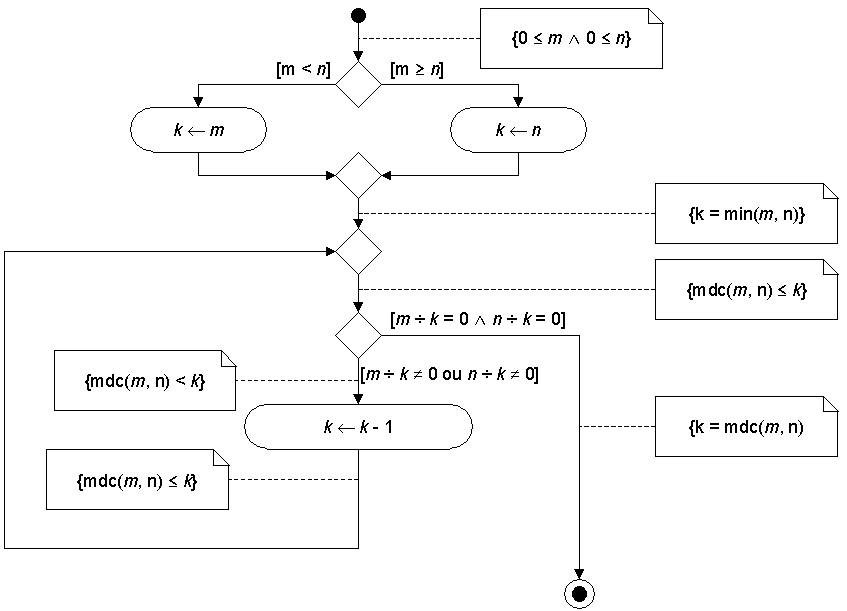
Primeiro, observem que admitimos que, logo no início, 0 < m e 0 < n.
Como esta é uma condição que se admite ser válida no início, chamamos-lhe pré-condição:
Dizer o que são comentários: notas que não afectam o cozinhado, mas que são justificações para o cozinheiro interessado.{PC: m e n são inteiros positivos.}
se m < n entãok <- m
senãok <- nenquanto m ÷ k <> 0 ou n ÷ k <> 0 faça-se:
k <- k - 1
O que é que sabemos depois do SE? Que k contém o menor dos dois valores. Ou seja
Explicar colocação de comentários com asserções entre as instruções do algoritmo.{PC: m e n são inteiros positivos.}
se m < n entãok <- m
senãok <- n
{k = min(m, n)}enquanto m ÷ k <> 0 ou n ÷ k <> 0 faça-se:
k <- k - 1
Mas isso significa que mdc(m, n) <= k. É óbvio? Não? Imaginemos que não. Então k = min(m, n) < mdc(m, n). Ou seja, o máximo divisor comum é maior que o menor dos valores! Absurdo. Donde só pode ser mdc(m, n) <= k.
Suponham agora que a condição do enquanto é falsa. Isso significa que m ÷ k = 0 e n ÷ k = 0. Ou seja, que k é divisor de m e n. Mas como começámos com mdc(m, n) <= k, então k tem de ser k = mdc(m, n). Porquê? Se não fosse igual então k seria maior que o mdc(m, n) e k dividiria m e n. Ou seja, haveria um divisor k de m e n maior que o máximo divisor comum de m e n. Absurdo!
Ou seja, se a condição do enquanto for falsa, então k é o máximo divisor comum procurado.
E se essa condição, chamada guarda do enquanto, for verdadeira? Então sabemos que mdc(m, n) <= k e que k não é divisor de m e n simultaneamente. E então? Que se tira daqui? Se não é divisor, também não é máximo divisor comum! Então k só pode ser maior que o mdc(m, n). Isso significa que k é grande demais e portanto deve ser diminuído. Retiremos uma unidade a k. Depois dessa operação já não podemos afirmar que mdc(m, n) < k. Mas podemos dizer que mdc(m, n) <= k!
Aqui talvez seja útil dizer que dizer x < k é o mesmo que dizer que x <= k - 1, desde que se esteja a tratar com inteiros!
Notem que recuperámos a condição que sabíamos válida antes do enquanto: mdc(m, n) <= k. Ou seja, o ciclo está construído de tal forma que essa condição se mantém..... Daí que a essa condição se chame condição invariante do enquanto.
Isto chega para demonstrar que, se o algoritmo alguma vez terminar, termina com o valor correcto. Mas não demonstra que termina sempre. Saber que termina para o caso 12 8 nada nos diz acerca do caso 1000001 20304996! Como demonstrá-lo?
Neste caso é simples. k começa sempre com o menor dos valores m e n, que é um inteiro positivo. Em cada passo da repetição o valor de k diminui de um. É fatal, portanto, que k atinja 1. Acontece que 1 é divisor de todos os inteiros positivos, e portanto também de m e n. Nessa altura a guarda do enquanto é falsa e o algoritmo termina.
Mas esquecemo-nos de uma coisa. Já temos um algoritmo em português, mas será que podemos ensinar o computador a resolver este problema em português? Como quem diz: "olha, para achares o máximo divisor comum de dois inteiros positivos m e n, pegas no menor deles e pões em k, depois, enquanto k não dividir algum desses inteiros, vais-lhe subtraindo um. Quando terminares, k será o máximo divisor comum de m e n". Infelizmente não. Os computadores não falam português.
O português é uma linguagem natural. Os computadores ainda não são fluentes em linguagem natural. Que "falam" eles, então? linguagem máquina. É uma linguagem muito básica. Tão básica, que é muito desagradável exprimirmo-nos nela. Vocês vão falar de linguagem máquina em Arquitectura de Computadores.
Então, se não podemos usar linguagem natural, nem queremos usar linguagem máquina, o que é que usamos? Uma linguagem da programação de alto nível, i.e., algo que, não sendo uma linguagem natural, com as suas imprecisões e ambiguidades, apesar disso não seja penoso para um humano "falar".
A linguagem de programação que vamos usar é o C++. O computador não percebe directamente C++. Há um programa, chamado compilador, que traduz de C++ para linguagem máquina.
Nota importante:
O nosso objectivo é ensinar-vos a programar. Usamos o C++ como poderíamos usar muitas outras linguagens. Este não é um curso de C++!
Um programa é a concretização de um algoritmo numa linguagem de programação.
Então é preciso concretizarmos o nosso algoritmo em C++. Ou seja, temos de escrever um programa correspondente ao algoritmo. O programa é assim:
Fazer explicação breve do programa.
#include <iostream>
using namespace std;
int main(){cout << "Introduza dois inteiros positivos: ";int m, n;cin >> m >> n;
int k;if(m < n)k = m;elsek = n;
while(m % k != 0 or n % k != 0)--k;
cout << "O máximo divisor comum de " << m << " e " << n << " é "<< k << endl;}
Quais são as fases de resolução de um problema, então?
O que é importante reter desta aula é: