Guião da 5ª Aula Teórica

Sumário

Sobrecarga de nomes de rotinas. Noção de assinatura. Utilizações.
Rotinas recursivas. Problemas. Garantia de fim. Aplicações.
Mecanismo de invocação de rotinas. A pilha, as variáveis locais, os parâmetros e o valor devolvido. Porque funcionam as rotinas recursivas.

Fazer a aula lenta. Começar por revisão curta.

Numa das aulas anteriores vimos as operações básicas do C++: as aritméticas, como a soma, as relacionais, as lógicas, etc. Esses operadores têm um característica curiosa: têm formas de cálculo diferentes para tipos diferentes de operandos. Pense-se no operador /. Se os operandos forem de vírgula flutuante, a divisão é a usual (embora inevitavelmente aproximada). Mas, se forem de um tipo inteiro, a divisão é a divisão inteira. Por exemplo:

cout << 1 / 2 << endl;

escreve

0

enquanto

cout << 1.0 / 2.0 << endl;

escreve

0.5

Na realidade há várias operações de divisão: para short int, int, long int, os respectivos unsigned, para float, double, e long double. O C++ sabe que operação usar de acordo com o tipo dos operandos. "E então?", perguntam vocês. É que uma das formas de ver a escrita de rotinas em C++ é como estendendo as operações básicas do C++: como o C++ não possui operação para calcular o máximo divisor comum, escreveu-se uma função para o efeito. Mas se as rotinas são extensões das operações básicas do C++, será possível também ter várias rotinas diferentes em que varia o tipo dos parâmetros? A resposta é sim.

Suponha-se que se pretendia escrever uma função para calcular o quadrado de um inteiro (int). A solução óbvia é:

int quadradoDe(int const valor)
{
return valor * valor;
}

E se se pretender o quadrado de um valor de vírgula flutuante? Então a solução é:

double quadradoDe(double const valor)
{
return valor * valor;
}

E se for um unsigned long?

unsigned long quadradoDe(unsigned long const valor)
{
return valor * valor;
}

Mas isto não viola a regra de que, em cada contexto, só se pode ter uma rotina com o mesmo nome? (Sim, a regra também é válida para rotinas, embora com umas subtilezas). Sim e não. Acontece que a regra diz que não pode existir mais do que uma rotina com a mesma assinatura!

O que é a assinatura duma rotina? É a sequência constituída por nome e lista dos tipos dos parâmetros.

As assinaturas das funções acima são:

quadradoDe, int
quadradoDe, double
quadradoDe, unsigned long

Neste caso as assinaturas variam apenas nos tipos. Estas funções dizem-se sobrecarregadas. A invocação é feita como usual, sendo a versão da função chamada dependente do tipo dos argumentos:

cout << quadradoDe(10) << endl; // versão int.
cout << quadradoDe(10.0) << endl; // versão double.
cout << quadradoDe(10UL) << endl; // versão unsigned long.

Ou ainda:

int somaDe()
{
    return 0;
}

int somaDe(int const a)
{
    return a;
}

int somaDe(int const a, int const b)
{
    return a + b;
}

int somaDe(int const a, int const b, int const c)
{
    return a + b + c;
}
int somaDe(int const a, int const b, int const c, int const d)
{
    return a + b + c + d;
}

As assinaturas das funções acima são:

somaDe somaDe, int somaDe, int, int
somaDe, int, int, int
somaDe, int, int, int, int

Neste caso as assinaturas variam no número de parâmetros.

Que aparece após

cout << somaDe() << endl;         // versão 0 parâmetros.
cout << somaDe(1) << endl;          // versão 1 parâmetro.
cout << somaDe(1, 2) << endl;       // versão 2 parâmetros.
cout << somaDe(3, 2, 1) << endl;    // versão 3 parâmetros.
cout << somaDe(0, 3, 1, 2) << endl; // versão 4 parâmetros.

Eles que respondam.

Este problema resolvia-se também facilmente com os parâmetros com argumentos por omissão:

int somaDe(int const a = 0, int const b = 0, int const c = 0, int const d = 0)
{
return a + b + c + d;
}

Explicar muito brevemente.

Mas os assuntos principais desta aula são outros. Vamos falar sobre recursividade e pormenorizar o mecanismo de invocação e retorno de rotinas.

Suponhamos que pretendíamos escrever uma função para calcular o factorial.

Quem é que sabe o que é o factorial?

Discutir. Concluir que:

n! = n × n-1 × ... × 1
n! = (P i : 1 <= i <= n : i)

Usar notação usual do produto (explicar por analogia com o somatório) e colocar também a notação acima. Discutir soma e produto de zero termos: elementos neutros.

Será que eu posso definir o factorial duma forma recorrente, i.e., definir n! à custa de (n-1)! ?

n! = ... (n-1)! ....

Discutir.

Por exemplo

4! = 4 × 3 × 2 × 1 = 4 × (3 × 2 × 1)

Hmmm.... Então:

n! = n × (n-1)!

Esta definição é válida sempre? E se n for 0?

0! = 0 × (-1)! = 0 ??????????

Não! A definição só é válida para n > 0! Então

n! = n × (n-1)! se n > 0

E para valores mais pequenos? Para negativos, o factorial não está definido. Logo sobra-nos o factorial de 0 que é...

n! = 1 se n = 0

Logo, a definição recorrente completa é:

n! = n × (n-1)! se n > 0
n! = 1 se n = 0

Voltemos à nossa função. Chamemos-lhe factorialDe(). Comecemos por escrever o que já sabemos:

? factorialDe(?)
{
?
}

Começámos por escrever o esqueleto do cabeçalho da função com o que já sabemos (o seu nome), e construímos a "caixa" onde se vai guardar o "mecanismo" da função. Que sabemos mais?

Discutir. Concluir que é importante começar por clarificar o que a função calcula.

A função calcula o factorial, vamos deixar isso bem claro escrevendo o comentário da praxe antes do cabeçalho da função:

/** Devolve o factorial do inteiro não negativo passado como argumento.
    @pre 0 <= n.
    @post factorialDe = n!.*/
? factorialDe(?)
{     assert(?);

    ?
}

Aproveitamos logo para colocar o esqueleto da respectiva asserção.

Quantos parâmetros deve ter a função? De que tipo? Que tipo de valor devolve?

Esperar respostas.

Exacto! Tem um parâmetro inteiro e devolve um inteiro. Que tipo de inteiro? Podemos admitir que é um int. Logo

/** Devolve o factorial do inteiro não negativo passado como argumento.
    @pre 0 <= n.
    @post factorialDe = n!.*/
int factorialDe(int const n)
{
    assert(0 <= n);

    ?
}

Aproveitamos para completar a asserção.

Falta pois o "como a função funciona"... Será que a definição recorrente nos ajuda?

Discutir com eles. Sugerir aplicação directa.

/** Devolve o factorial do inteiro não negativo passado como argumento.
@pre 0 <= n.
@post factorialDe = n!.*/
int factorialDe(int const n)
{
    assert(0 <= n);
    if(n == 0)
        return 1;
    else
        return ?;
}

Discutir o que a função deve devolver se o n for > 0. Sugerir de novo aplicação da definição recorrente.

Então a solução é

/** Devolve o factorial do inteiro não negativo passado como argumento.
    @pre 0 <= n.
    @post factorialDe = n!.*/
int factorialDe(int const n)
{
    assert(0 <= n);

    if(n == 0)
        return 1;
    else
        return n * factorialDe(n - 1);
}

É um exemplo de uma função recursiva. Uma rotina é recursiva se se invocar ou chamar a si própria!

Vamos agora fazer um programa de teste da função e fazer um traçado da sua execução.

#include <iostream>

using namespace std;
/** Devolve o factorial do inteiro não negativo passado como argumento.
    @pre 0 <= n.
    @post factorialDe = n!.*/
int factorialDe(int const n)
{
    assert(0 <= n);
    if(n == 0)                         // 1
        return 1;                      // 2
    else
                   factorialDe(n - 1) //3A
        return n *                 ;   // 3B
}
int main()
{
            factorialDe(3)             //4A
    cout <<                << endl;    // 4B
}

Vamos fazer um traçado.

Fazer um traçado em que as variáveis são caixas UML no contexto das funções. Quando se chega à segunda chamada da função factorial fica uma dúvida: a constante n da primeira chamada ainda não foi destruída (a função ainda não retornou), mas deve ser construída uma nova constante n...

A regra diz que as variável e constantes locais são por omissão automáticas, e portanto são construídas quando a sua instrução de definição é executada ou, no caso dos parâmetros, quando a função começa a ser executada, e são destruídas quando a execução abandona o contexto da sua definição...

Então ficam duas versões da constante (do parâmetro n) construídas!

Se não houver tempo, passar directamente ao exemplo com o factorial!

O.k.. Alto. Vamos voltar a trás, que isto está a ficar confuso. Vamos descrever um pouco mais em pormenor o mecanismo de invocação de rotinas, e já voltamos ao factorial. Seja o programa:

#include <iostream>

using namespace std;
int somaDe(int const a, int const b)
{
return a + b;
}
int main()
{
cout << soma(1, 2) << endl;
}

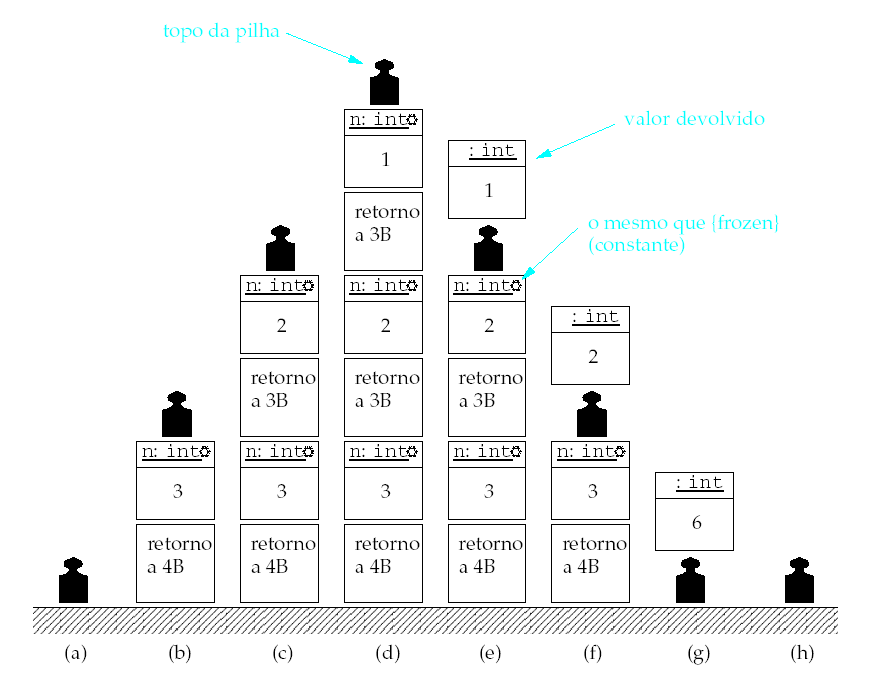
O computador, para manter a casa arrumada durante a invocação de rotinas, usa uma pilha. Uma pilha é uma estrutura onde se acumulam coisas, de baixo para cima, de modo que só se tem acesso directo ao topo. Como uma pilha de pratos.

Aqui recomendo que se use uma notação idêntica à que está nas folhas teóricas, embora com fios ligando às instruções de retorno! Ver abaixo.

Esta nossa pilha (desenhar no quadro a pilha vazia com o pisa-papeis) guarda variável locais (caixas UML), locais de retorno (caixas com um fio ligando à instrução de retorno), valores devolvidos (caixas UML sem nome), e tem um pisa-papeis a assinalar o topo... (ver abaixo)

Nota: Na realidade, é comum que o endereço de retorno seja colocado na pilha depois dos parâmetros! É o que acontece no MAC-1. No final da aula referir que assim é. Quando houver oportunidade, alterar as folhas teóricas e o guião de modo a usarem a ordem correcta.

Vamos ver como isto funciona. Quando o programa é executado, é invocada a função main(). Etc.

Seguir a sequência para os dois exemplos! Os fios são para não nos perdermos! É importante frisar que:

Em cada instante podem existir na pilha muitas variáveis e constantes, inclusive com o mesmo nome! As únicas visíveis são as que estão desde o topo da pilha até o primeiro fio de retorno.
Os valores devolvidos ficam acima do topo da pilha (pisa-papeis) e por isso "voam com o vento".
A pilha termina sempre tal como começou.

Perfeito. Vimos que é possível escrever funções recursivas e qual o mecanismo de invocação de funções que as tornam possíveis. Tudo o que dissemos sobre funções é válido para procedimentos, só que os procedimentos não devolvem nada!

A recursividade introduz com frequência grandes ineficiências nos programas, devido aos trabalhos de arrumação da casa usando a pilha. São preferíveis em geral soluções iterativas, com ciclos, que estudaremos formalmente mais tarde. Tal como no uso de ciclos, há uma questão que não pode ser esquecida: será que as chamadas recursivas terminam sempre? Que se passa no caso do factorial?

Discutir o que acontece quando n é negativo! Perguntar o que aconteceria sem a asserção!

Daqui para baixo não é importante. Se for possível, óptimo. Se não, não faz mal.

Serão capazes de escrever uma função recursiva para calcular a potência de um número? Qual a forma recorrente de definir xⁿ? Que tipos têm de ter x e n? Ou seja, a que conjuntos pertencem? Porquê?

Discutir e desenvolver. Discutir PC. Ou 0 <= n ou x <> 0. Dizer que vamos resolver apenas quando 0 <= n.

Ou seja,

PC: 0 <= n.
CO: potênciaDe = xⁿ.

Desenvolver:

/** Devolve a potência inteira de um número.    @pre 0 <= n.    @post potênciaDe = xⁿ.*/double potênciaDe(double const x, int const n)
{     assert(0 <= n);

    if(n == 0)
        return 1.0;
    else
        return x * potênciaDe(x, n - 1);
}

Pode-se deixar n < 0? Que é necessário fazer?

/** Devolve a potência inteira de um número.    @pre 0 <= n ou x <> 0.    @post potênciaDe = xⁿ.*/double potênciaDe(double const x, int const n)
{     assert(0 <= n or x != 0);

    if(n == 0)
        return 1.0;
    else
        return x * potênciaDe(x, n - 1);
}

Desenvolver:

/** Devolve a potência inteira de um número.    @pre 0 <= n ou x <> 0.    @post potênciaDe = xⁿ.*/double potênciaDe(double const x, int const n)
{
    assert(0 <= n or x != 0);

    if(0 < n)
        return x * potênciaDe(x, n - 1);
    else
        if(n < 0)
            return 1.0 / potênciaDe(x, -n);
        else
            return 1.0;
}