Guião da 7ª Aula Teórica

Sumário

  1. Instrução while: sintaxe e semântica.
  2. Exemplo de ciclos simples.
  3. Inicialização, guarda, passo (acção e progresso).
  4. Condição invariante.
  5. Demonstração da correcção de ciclos.  Sua importância.
  6. Importância da fraqueza das guardas.

Introduzir sintaxe do while:

while(G)
    passo

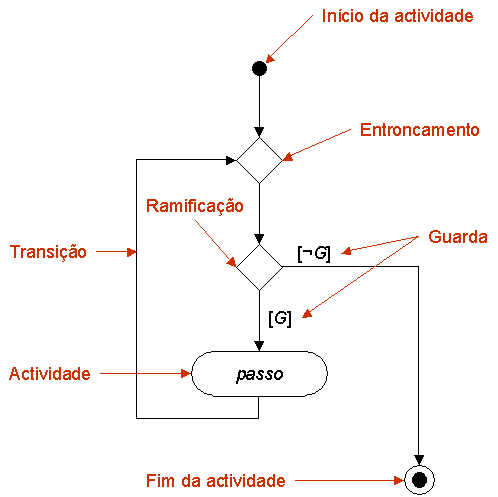
Fazer diagrama de actividade.  Não esquecer de dizer os nomes dos elementos: actividade, transição, entroncamento, ramificação, guarda, comentário, asserção, início da actividade global e fim da actividade global.

Exemplo: função potênciaDe().

double potênciaDe(double const x, int const n)
{
    int i = 1;
    double potência = x;

    while(i <= n) {
        potência *= x;
        ++i;
    }

    return potência;
}

Está certo?  Em que resulta a chamada potênciaDe(2.0, 3)?  Tudo bem?  

Fazer traçado!

Não!

Qual é o problema?

Discutir com eles.

O problema é a guarda ser i <= n!  Está errada!

Corrigir para i < n:

double potênciaDe(double const x, int const n)
{
    int i = 1;
    double potência = x;

    while(i < n) {
        potência *= x;
        ++i;
    }

    return potência;
}

Um belo dia alguém chama potênciaDe(5.0, 0) e o resultado é.........

Fazer traçado.

5,0

Errado!

Qual é o problema?  

Discutir.

A inicialização está errada!

Corrigir inicialização:

double potênciaDe(double const x, int const n)
{
    int i = 0;
    double potência = 1.0;

    while(i < n) {
        potência *= x;
        ++i;
    }

    return potência;
}

Verificar de novo.

A estrutura normal de um ciclo usando a instrução de iteração while é

inic (inicialização)
while(G)
    passo

onde passo é normalmente

{
    acção
    prog (progresso)
}

Desenhar o respectivo diagrama de actividade no quadro explicando.  Pode-se aproveitar o desenho anterior.

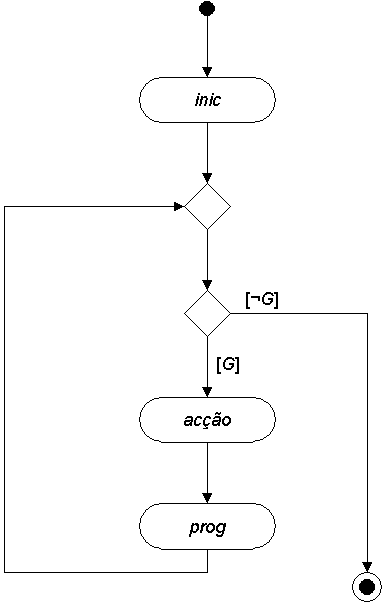
O progresso é o que faz o ciclo progredir em direcção ao seu fim.  A acção é o que é necessário repetir.

Outro belo dia alguém chama potencia(2.0, -1).  Qual é o problema?

Discutir...

Aqui o problema ou está na pré-condição, que não especificámos!, ou na implementação da função.

Explicar diferença.  Dizer que, mais uma vez, deveríamos ter começado por especificar a função, escrevendo o respectivo comentário de documentação.  Optar artificialmente pelas PC:

/** Devolve a potência n de x.
    @pre 0 <= n.
    @pre potênciaDe = xn. */
double potênciaDe(double const x, int const n)
{
    int i = 0;
    double potência = 1;

    while(i < n) {
        potência *= x;
        ++i;
    }

    return potência;
}

Justificar guarda fraca:

Se se usar i != n e o utilizador puser n < 0 o ciclo fica infinito!  O que é preferível?

Discutir...

É preferível um ciclo infinito a um resultado errado!

/** Devolve a potência n de x.
    @pre 0 <= n.
    @pre potênciaDe = xn. */
double potênciaDe(double const x, int const n)
{
    int i = 0;
    double potência = 1;

    while(i != n) {
        potência *= x;
        ++i;
    }

    return potência;
}

Apesar disso continua a ser útil usar instruções de asserção:

/** Devolve a potência n de x.
    @pre 0 <= n.
    @pre potênciaDe = xn. */
double potênciaDe(double const x, int const n)
{
    assert(0 <= n);

    int i = 0;
    double potência = 1;

    while(i != n) {
        potência *= x;
        ++i;
    }

    return potência;
}

É a chamada "programação com cinto, ligas e suspensórios".

Moral desta estória:

  1. Escrever sempre a especificação da função!
  2. É importante demonstrar que os ciclos estão correctos.

Desenhar diagrama de actividade do ciclo.

Acrescentar numeração das transições ao código:

/** Devolve a potência n de x.
    @pre 0 <= n.
    @pre potênciaDe = xn. */
double potênciaDe(double const x, int const n)
{
    assert(0 <= n);
1
    int i = 0;
    double potência = 1;
2
    while(i != n) {
3
        potência *= x;
        ++i;
 4
    }
5
    return potência;
}

Dizer para eles colocarem a asserção mais forte possível em cada transição.  É importante dizer que as asserções dizem respeito aos valores das instâncias, ou seja, das constantes e variáveis do programa.

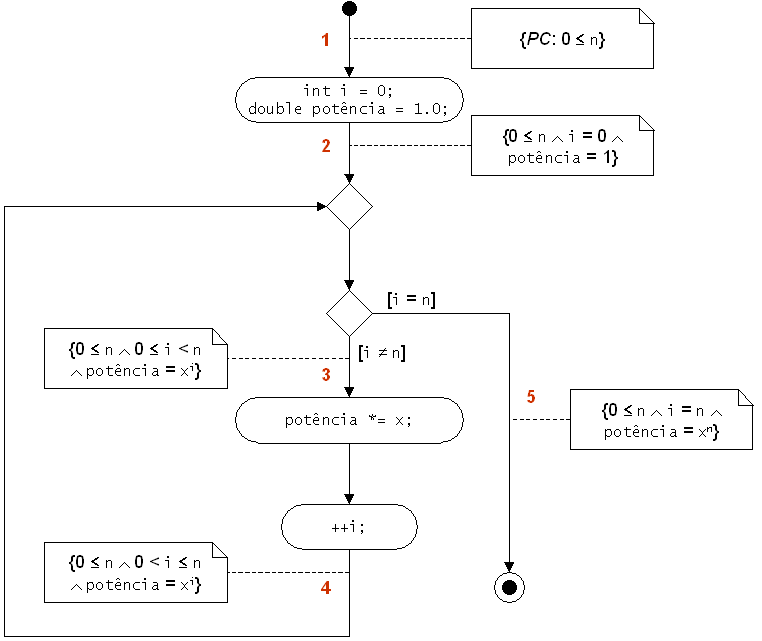
Explicar o que é uma condição invariante:

Uma condição é um invariante de um ciclo se for verdadeira depois da inicialização, antes e depois do passo, e depois do ciclo.  Ou seja, se for verdadeira durante todo o ciclo.

Tentar fazê-los chegar à condição invariante!  Normalmente as condições invariantes mais interessantes são o mais forte possível (desde que envolvendo as variáveis relevantes para o ciclo).  A cada asserção corresponde o conjunto dos valores de instâncias que levam à sua veracidade.  A condição invariante deve corresponder à união dos conjuntos correspondentes às asserções nas transições 2, 3, 4 e 5.

Para facilitar a obtenção da condição invariante fazer uma tabela com o traçado da função quando executada com x = 4 e n = 3:

 

Transição i potência
2 0 1,0
3 0 1,0
4 1 4,0
3 1 4,0
4 2 16,0
3 2 16,0
4 3 64,0
5 3 64,0

Discutir e concluir que é:

CI: 0 <= i <= n e potência = xi.

O esquema de demonstração de correcção de um ciclo é o seguinte:

  1. descobrir a condição invariante CI, 
  2. provar que init estabelece a veracidade da condição invariante CI,
  3. provar que CI e G seguida do passo implica CI, e
  4. provar que CI e ¬G implica CO.

No fundo é uma demonstração por indução: demonstra-se que a condição invariante é verdadeira no início e que, se CI for verdadeira numa iteração, então também é verdadeira na próxima, ou seja, é verdadeira sempre.

Discutir isto no diagrama.

Fazer demonstração usando atribuições.  Usar demonstração directa primeiro e invertida depois.  Dizer que a segunda é mais rigorosa, mas a primeira em geral é mais simples, pelo que a devem usar e treinar na aula prática.  Explicar que a vantagem da demonstração inversa é principalmente para o desenvolvimento de ciclos.

A demonstração inversa parte dos objectivos, o que é mais natural em programação.  Por outro lado, existe uma forma simples de obter a pré-condição mais fraca de uma atribuição, dada a respectiva condição objectivo.  Não existe, por outro lado, nenhuma regra simples para obter a condição objectivo mais forte de uma atribuição dada a respectiva pré-condição.

Dizer outra vez que pós-condição é o mesmo que condição objectivo (CO e não PC).  Demonstração directa é a obtenção da pós-condição mais forte.

Está demonstrada a correcção?  Não!  Demonstrámos apenas que, se o ciclo terminar alguma vez, termina com o valor correcto.  A isto chama-se correcção parcial.

E o ciclo termina sempre?

Discutir e demonstrar informalmente (i começa em zero, e 0 <= n pela pré-condição).

O tempo gasto a perceber bem um problema é poupado por não se ter de detectar e corrigir erros.  Além disso gasta-se esse tempo uma vez apenas.  No futuro é só reutilizar o código desenvolvido, que sabemos correcto.

O nosso objectivo não é ensinar C++: é ensinar a programar.  Logo, na próxima aula falaremos de como desenvolver ciclos correctos.

Se houver tempo voltar à potência.  Eliminar restrições de PC.  Pedir sugestões.  Quais as combinações da entrada aceitáveis?  Que corpo usar?

/** Devolve a potência n de x.
    @pre 0 <= n ou x <> 0,0. 
    @pre potênciaDe = xn. */
double potênciaDe(double const x, int const n)
{
    assert(0 <= n or x != 0);

    int base = n < 0 ? 1.0 / x : x;
    int expoente = n < 0 ? -n : n;

    int i = 0;
    double potência = 1;

    while(i != nexpoente) {
        potência *= xbase;
        ++i;
     }

    return potência;
}

Fazer pequena perora sobre as vantagens da disciplina.  Mas alertar que nem sempre é fácil ser muito preciso.  Há que tentar, no entanto.

Finalmente, convém realçar que:

  1. As pré-condições das rotinas querem-se tão fracas quanto possível, pois isso facilita a vida do... consumidor da rotina, embora torne a vida do produtor mais complicada.  Pré-condição ideal: V.
  2. As condições objectivo das rotinas querem-se tão fortes quanto possível, pois isso aumenta a utilidade das rotinas para o consumidor, embora torne a vida do produtor mais complicada.
  3. As guardas dos ciclos querem-se tão fracas quanto possível, de modo a que os ciclos sejam infinitos em caso de violação da respectiva pré-condição.  Isto facilita a vida do programador produtor, pois detecta mais facilmente erros de programação.
  4. As condições invariantes dos ciclos querem-se tão fortes quanto possível, pois de outra forma não ajudarão à demonstração da sua correcção.  Uma condição invariante forte explica o respectivo ciclo.

Qual a condição mais fraca?  Aquela que se verifica sempre: V.

Qual a condição mais forte?  Aquela que nunca se verifica: F.

Que significa uma condição A ser mais forte que outra B?  Significa que A implica B!  Significa que o conjunto dos valores que levam à verificação de A está contido no conjunto de valores que levam à veracidade de B.  Logo:

  1. A condição V corresponde ao universo, ou conjunto universal.
  2. A condição F corresponde ao conjunto vazio.

Esta parte não é para dar.  Serve apenas para mostrar como se pode fazer uma demonstração quando se usam valores lidos do canal de entrada.

Se houver tempo, escrever CI para o procedimento seguinte e demonstrar correcção.  Referir que ser informal não é necessariamente errado.

int somaLidosNãoNegativos()
{
    int soma = 0;
    int v;
    cin >> v;
    while(v >= 0) {
        soma += v;
        cin >> v;
    }
    return soma;
}

PC: O utilizador escreve uma sequência de inteiros em que existe pelo menos um negativo.

CO: soma = soma de todos os inteiros não negativos lidos até ao primeiro negativo (exclusive).

CI: soma = soma de todos os inteiros lidos com excepção do último e todos os inteiros lidos com excepção do último são não-negativos

CI e ¬G implica CO?

CI e ¬G: soma = soma de todos os inteiros lidos com excepção do último e todos os inteiros lidos com excepção do último são não-negativos e último lido é negativo. 

É óbvio que implica CO.  Porquê?  Porque então o último lido foi o primeiro negativo e a soma acumulou os anteriores.

int soma = 0;
int v;
cin >> v;
// implica CI?  Claro.

CI e G + passo implica CO?

// CI e G: soma = soma de todos os inteiros lidos com excepção do último e todos os
//        inteiros lidos com excepção do último são não-negativos e último é não-negativo.
soma += v;
// soma = soma de todos os inteiros lidos e todos os inteiros lidos são não-negativos e
//       último é não-negativo.
cin >> v;
// Há um novo último!
// soma = soma de todos os inteiros lidos com excepção do último e todos os inteiros
//       lidos com excepção do último são não-negativos e penúltimo é não-negativo.
// implica CI.