Guião da 8ª Aula Teórica

Sumário

1. Importância da especificação do problema: as soluções são por vezes mais simples do que a formulação inicial do problema deixa antever.
2. Noção de invariante de um ciclo.
3. Condição invariante, inicialização e guarda de um ciclo.
4. Metodologia de Dijkstra para desenvolvimento de ciclos:

1. obtenção da CI: enfraquecimento da CO por introdução de variável.  Menção ao enfraquecimento por factorização da CO.
2. obtenção da guarda.
3. inicialização
4. progresso
5. acção

5. Importância da metodologia: base formal para desenvolvimento, controlo dos erros, redução de surpresas, melhor raciocínio, maior eficiência.
6. Prática da construção de ciclos: usar ou não usar metodologia?

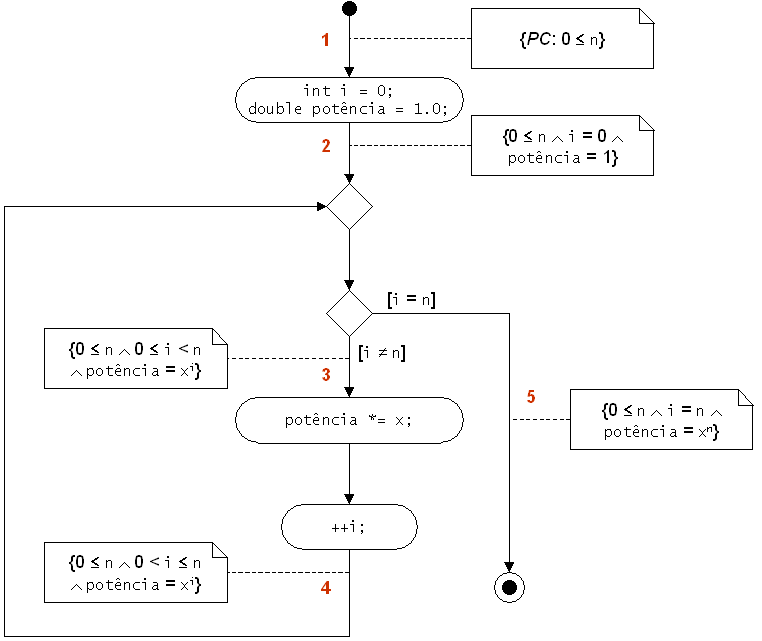
Começar por escrever no quadro a função da aula anterior e o respectivo diagrama de actividade com as asserções mais fortes em cada transição importante:

/** Devolve a potência n de x.
    @pre 0 <= n.
    @post potênciaDe = xn. */
double potênciaDe(double const x, int const n)
{
    assert(0 <= n);

    double potência = 1.0;
    int i = 0;

    while(i != n) {
        potência *= x;
        ++i;
    }

    return potência;
}

Na aula anterior vimos a importância do formalismo na demonstração de correcção de ciclos: os ciclos são parte importante da escrita de algoritmos e não é possível na prática demonstrar a sua correcção recorrendo a testes.

Na demonstração de correcção de ciclos têm um papel importante os chamados invariantes, ou condições invariantes.

Uma condição invariante de um ciclo é uma condição que é verdadeira desde o início ao fim do ciclo.  Claro está que cada ciclo tem uma infinidade de invariantes.  Em geral a condição invariante mais interessante é o mais forte possível, desde que inclua apenas variáveis envolvidas no ciclo.

Regressemos por um instante ao exemplo da aula passada.

Assinalar no código e no diagrama inic, passo, acção e prog.  Explicar de novo as asserções mais fortes.  Dizer que a condição invariante é a condição mais forte que se verifica durante todo o ciclo.  Fazê-los determiná-la de novo.

É importante perceber que a condição invariante nos diz muito acerca do ciclo: não é apenas uma expressão matemática, tinta sobre um quadro branco.  Neste caso diz-nos que

Durante todo o ciclo a variável potência contém xi, estando sempre i entre 0 e n inclusive.

Mas haverá alguma forma de desenvolver os ciclos com maior rigor desde o início, em vez de os desenvolver ao sabor da pena para só depois verificar a sua correcção?

Há!  Chama-se Metodologia de Dijkstra, e dá boas pistas para desenvolver ciclos.  Naturalmente não é um método infalível nem tão pouco substitui a criatividade e o engenho...

Escrever o nome Dijkstra no quadro.

Primeiro o Sr. Dijkstra.  Este senhor, dono de um nome com uma pronúncia tão estranha, era holandês e foi um dos fundadores da programação disciplinada.  Morreu no verão de 2002.  Se a programação é uma ciência, deve-o em grande medida a este senhor.  Se é uma arte, deve-o em grande medida ao Sr. Knuth, de quem já falámos.

Façamos uma analogia, algo perigosa, entre programar e conduzir.  Naturalmente que é possível aprender a conduzir e a programar sem professor.  As grandes desvantagens do autodidactismo são o tempo que se demora a aprender, e os erros que se aprende a cometer e que poderão ser difíceis de corrigir a posteriori (além de poderem ser fatais...).  Admitamos, pois, que há ensino...

Quando se aprende a conduzir é conveniente que o instrutor dê noções acerca do funcionamento do automóvel e indique a sequência de passos a realizar para fazer alguma manobra.  O curioso é que enquanto instruendos estamos muito conscientes desses passos mas, à medida que vamos aprendendo, vamo-los "entranhando", até que conseguimos conduzir quase sem pensar nisso, reservando a nossa atenção concentrada apenas para as manobras menos usais ou para as situações mais perigosas.

De facto, como o Fernando Pessoa dizia da Coca-Cola:

Primeiro estranha-se.  Depois entranha-se.

O mesmo deve acontecer em programação.  Espero que esta metodologia, que vão começar por estranhar, vos ponha a pensar e que entranhem o que dela é essencial, para que a apliquem sem pensar nisso sempre que tenham de escrever um ciclo simples, e que recorram a ela em circunstâncias mais complicadas.

A metodologia de Dijkstra tem dois pontos fundamentais:

1. Baseia-se na condição objectivo: a programação é uma actividade orientada pelos objectivos!
2. Começa por tentar determinar uma boa condição invariante: a condição invariante é central na metodologia.

inic (inicialização)
while(G) {
    acção
    prog (progresso)
}

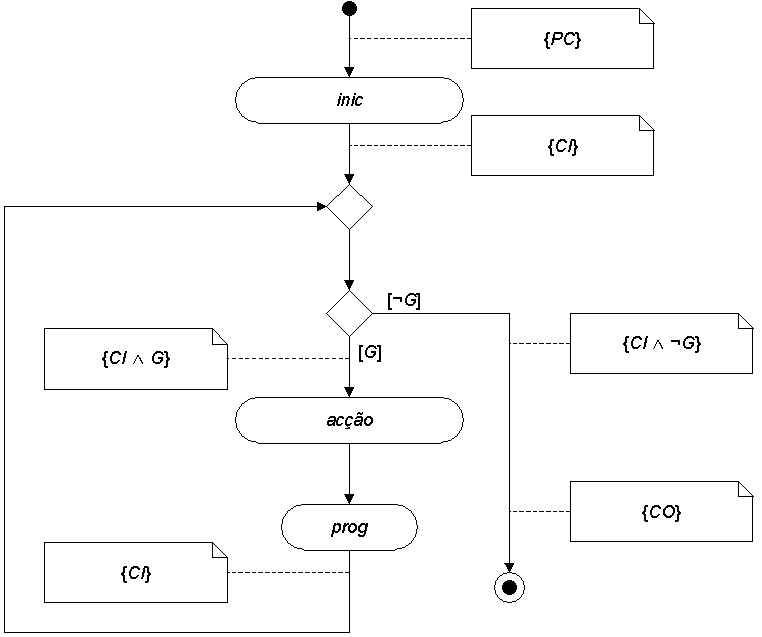
Vamos aplicar esta metodologia de desenvolvimento a dois exemplos simples:

1. Calcular a soma dos primeiros n ímpares positivos.
2. Calcular a "raiz inteira", que é melhor aproximação inteira por defeito da raiz de um número.

Dividir o quadro ao meio

A metodologia diz o seguinte:

Ir escrevendo os passos no quadro à medida que são aplicados no desenvolvimento dos dois exemplos.  Os passos correspondem aos títulos das secções abaixo.

Dividir resto do quadro ao meio e ir desenvolvendo ambos os problemas.

Vamos reservar estes cantinhos para escrever o código desenvolvido.  O resto do espaço vai ser usado para pensar acerca dos problemas...

Desenhar pequenos quadrados no canto superior direito de cada uma das duas partes.

Discutir estrutura e nome das funções.  Justificar variável r para simplificar as expressões.  Escrever as seguintes estruturas:

int somaDosPrimeirosÍmpares(int const n)
{
    int r = ?;

    ...

    return r;
}

int raizInteiraDe(int const x)
{
    int r = ?;

    ...

    return r;
}

1  Especificar o problema

Comecemos pela pré-condição.  Que restrições há que introduzir em cada um dos casos?

Discutir.  Concluir que não faz sentido falar na soma de um número negativo de termos.  Explicar de novo o que é a soma de zero termos.

Espero que seja claro que as pré-condições não parecidas, mas por razões inteiramente diferentes:

PC: 0 <= n.

PC: 0 <= x.

A condição objectivo neste caso é que a variável r contenha a soma dos primeiros n ímpares.  Ou seja:

Escrever na forma de um somatório.  Variável muda é j.  Discutir limites do somatório.  Explicar problemas da notação para a soma de 0 termos.  Explicar de novo notação alternativa.  Explicar cada um dos termos.

CO: r = (S j : 0 <= j < n : 2j +1).

Discutir.  Concluir, de novo, que a soma de zero termos é 0.

Logo, a estrutura da função é:

/** Devolve a soma dos primeiros n naturais ímpares.
    @pre 0 <= n.
    @post somaDosPrimeirosÍmpares = (S j : 0 <= j < n : 2j + 1). */
int somaDosPrimeirosÍmpares(int const n)
{
    assert(0 <= n);

    // 0 <= n.
    int r = ?;

    ...

    // CO: r = (S j : 0 <= j < n : 2j +1).
    return r;
}

Discutir.  Explicar deficiências à medida que surgem.  Explicar objectivo de novo.

Coloquemos aqui alguns exemplos, que nos podem ajudar a pensar:
 

Claramente a raiz não pode ser negativa:

0 <= r.

r <= x^½.

Isto ainda não chega.  Senão imaginem que x é 5 e r é 0...  Falta a parte do "melhor".  Temos de obter a melhor aproximação.

Discutir qual é o critério mais simples para r ser a melhor aproximação por defeito.  Concluir que é

x^½ < r + 1.

Logo, a condição objectivo é:

CO: 0 <= r <= x^½ < r + 1. 

Logo, a estrutura da função é:

/** Devolve a melhor aproximação por defeito de x^½.
    @pre 0 <= x.
    @post 0 <= raizInteiraDe <= x^½ < raizInteiraDe + 1. */
int raizInteiraDe(int const x)
{
    assert(0 <= x);

    // 0 <= x.
    int r = ?;

    ...

     // CO: 0 <= r <= x^½ < r + 1.

    assert(0 <= r and r * r <= x and x < (r + 1) *(r + 1));

    return r;
}

2  Será necessário um ciclo?

Fazer aviso dizendo que talvez não seja necessário usar ciclos em algum dos casos...

Podemos então colocar os esqueletos dos ciclos:

/** Devolve a soma dos primeiros n naturais ímpares.
    @pre 0 <= n.
    @post somaDosPrimeirosÍmpares = (S j : 0 <= j < n : 2j + 1). */
int somaDosPrimeirosÍmpares(int const n)
{
    assert(0 <= n);

    // 0 <= n.
    int r = ?;

    while(...) {
        ...
    }

    // CO: r = (S j : 0 <= j < n : 2j +1).
    return r;
}

/** Devolve a melhor aproximação por defeito de x^½.
    @pre 0 <= x.
    @post 0 <= raizInteiraDe <= x^½ < raizInteiraDe + 1. */
int raizInteiraDe(int const x)
{
    assert(0 <= x);

    // 0 <= x.
    int r = ?;

    while(...) {
        ...
    }

     // CO: 0 <= r <= x^½ < r + 1.

    assert(0 <= r and r * r <= x and x < (r + 1) *(r + 1));

    return r;
}

3 e 4  Obtenção da condição invariante e determinação da guarda

Programação é uma actividade orientada pelos objectivos: deve-se olhar para a condição objectivo e, enfraquecendo-a, obter a condição invariante.  Depois procura-se uma guarda que leve ao resultado pretendido, i.e., à condição objectivo, quando o ciclo terminar.

Muitas vezes é possível obter uma condição invariante para o ciclo substituindo uma constante presente na condição objectivo por uma variável criada para o efeito.  É o que acontece no caso da função somaDosQuadrados():

CO: r = (S j : 0 <= j < n : 2j + 1).

A primeira coisa a fazer é introduzir uma nova variável que vai substituir a constante n.  Chamemos-lhe i:

/** Devolve a soma dos primeiros n naturais ímpares.
    @pre 0 <= n.
    @post somaDosPrimeirosÍmpares = (S j : 0 <= j < n : 2j + 1). */
int somaDosPrimeirosÍmpares(int const n)
{
    assert(0 <= n);

    // 0 <= n.
    int i = ?;
    int r = ?;

    while(...) {
        ...
    }

    // CO: r = (S j : 0 <= j < n : 2j +1).
    return r;
}

CO': r = (S j : 0 <= j < i : 2j + 1).

O problema é que esta condição objectivo não é equivalente à anterior no que diz respeito ao resultado da função!  Que valor deverá ter a nova variável?

Discutir e concluir que deverá ser n.

CO': r = (S j : 0 <= j < i : 2j + 1) e i = n.

Escrever no código:

/** Devolve a soma dos primeiros n naturais ímpares.
    @pre 0 <= n.
    @post somaDosPrimeirosÍmpares = (S j : 0 <= j < n : 2j + 1). */
int somaDosPrimeirosÍmpares(int const n)
{
    assert(0 <= n);

    int i = ?;
    int r = ?;

    while(...) {
        ...
    }

    // CO': r = (S j : 0 <= j < i : 2j + 1) e i = n.
    // que implica CO: r = (S j : 0 <= j < n : 2j +1).
    return r;
}

A condição invariante do ciclo pode ser obtida enfraquecendo na nova condição objectivo, equivalente na prática à original, as restrições aos valores que a variável i pode tomar:

CI: r = (S j : 0 <= j < i : 2j + 1) e ? <= i <= ?.

CI: r = (S j : 0 <= j < i : 2j + 1) e 0 <= i <= n.

Esta escolha corresponde a enfraquecer a condição objectivo, pois a condição invariante aceita mais possíveis valores para a variável r do que a condição objectivo, que só aceita o resultado final pretendido.  Os valores aceites para essa variável pela condição invariante correspondem a valores intermédios durante o cálculo do valor final.  Neste caso correspondem a todas as possíveis somas de ímpares: desde a soma com zero termos até à soma com os n termos pretendidos.

A guarda pode ser obtida facilmente observando que no final do ciclo ela será forçosamente falsa e a condição invariante verdadeira (i.e., que CI e ¬G), e que se pretende, nessa altura, que a condição objectivo do ciclo seja verdadeira.  Ou seja, sabe-se que no final do ciclo

CI e ¬G: r = (S j : 0 <= j < i : 2j + 1) e 0 <= i <= n e ¬G.

e pretende-se que

CO': r = (S j : 0 <= j < i : 2j + 1) e i = n.

Discutir.  Concluir que é:

¬G: i = n,
ou seja,
G: i <> n.

pois nesse caso

CI e ¬G: r = (S j : 0 <= j < i : 2j + 1) e 0 <= i <= n e i = n.

ou seja,

CI e ¬G: r = (S j : 0 <= j < i : 2j + 1) e 0 <= n e i = n.

Que claramente implica a condição objectivo, pois é mais forte do que ela!

Vamos assinalar a condição invariante e a guarda no ciclo:

/** Devolve a soma dos primeiros n naturais ímpares.
    @pre 0 <= n.
    @post r = (S j : 0 <= j < n : 2j + 1). */
int somaDosPrimeirosÍmpares(int const n)
{
    // 0 <= n.

    int i = ?;
    int r = ?;

    // CI: r = (S j : 0 <= j < i : 2j + 1) e 0 <= i <= n.
    while(i != n) {
        ...
    }

    // CO': r = (S j : 0 <= j < i : 2j + 1) e i = n.
    // que implica CO: r = (S j : 0 <= j < n : 2j +1).
    return r;
}

Quando a condição objectivo é composta pela conjunção de várias condições, pode-se muitas vezes utilizar parte delas como negação da guarda ¬G e a parte restante como condição invariante.

Voltando à função raizInteiraDe(), é evidente que o corpo da função pode consistir num ciclo cuja condição objectivo já foi apresentada:

CO: 0 <= r <= x^½ < r + 1, ou seja
    0 <= r e r² <= x e x < (r + 1)².

Mas antes de o fazer temos de perceber como poderemos obter a guarda.  Uma forma simples de o fazer é simplesmente negar a conjunção dos termos que retirámos da condição objectivo para obter a condição invariante!  Confuso?  Nada, claro como água.  Imaginem que a condição objectivo é:

CO: A e B e C e D

e admitam que obtivemos a condição invariante seleccionando apenas os termos A e C.  Nesse caso:

CI: A e C

e os termos eliminados foram B e D.

Deve ser óbvio que a condição invariante é mais fraca que a condição objectivo.

Fazer analogia com intersecção de conjuntos para isto ficar claro.

Agora reparem na estrutura básica de um ciclo:

Mostrar o diagrama já desenhado.

No final do ciclo sabemos que 

CI e ¬G

e pretendemos que a condição objectivo seja verdadeira, ou seja,

CI e ¬G implica CO

Neste caso basta fazer ¬G: B e C para que CI e ¬G não apenas implica mas exactamente a condição objectivo!  Ou seja, a guarda é a negação da disjunção dos termos retirados para obter a condição invariante.

Voltando ao nosso caso:

CO: 0 <= r e r² <= x e x < (r + 1)².

Que manter na condição invariante e que deixar para a negação da guarda?

Discutir várias hipóteses.  Falar em possíveis inicializações!

Escolhendo para negação da guarda ¬G a condição x < (r + 1)², ou seja, escolhendo

G: (r + 1)² <= x,

CI: 0 <= r e r² <= x.

Vamos assinalar a condição invariante e a guarda no ciclo:

/** Devolve a melhor aproximação por defeito de x^½.
    @pre 0 <= x.
    @post 0 <= raizInteiraDe <= x^½ < raizInteiraDe + 1. */
int raizInteiraDe(int const x)
{
    assert(0 <= x);

    // 0 <= x.
    int r = ?;

    // CI: 0 <= r e r² <= x.
    while((r + 1) * (r + 1) <= x) {
        ...
    }

     // CO: 0 <= r <= x^½ < r + 1.

    assert(0 <= r and r * r <= x and x < (r + 1) *(r + 1));

    return r;
}

5  Determinação da inicialização

Qual a forma mais simples de inicializar i e r de modo que se verifique a condição invariante?

CI: r = (S j : 0 <= j < i : 2j + 1) e 0 <= i <= n.

Simples.  Basta inicializar ambas com zero:

/** Devolve a soma dos primeiros n naturais ímpares.
    @pre 0 <= n.
    @post r = (S j : 0 <= j < n : 2j + 1). */
int somaDosPrimeirosÍmpares(int const n)
{
    assert(0 <= n);

    // 0 <= n.
    int i = 0;
    int r = 0;

    // CI: r = (S j : 0 <= j < i : 2j + 1) e 0 <= i <= n.
    while(i != n) {
        ...
    }

    // CO': r = (S j : 0 <= j < i : 2j + 1) e i = n.
    // que implica CO: r = (S j : 0 <= j < n : 2j +1).
    return r;
}

CI: 0 = (S j : 0 <= j < 0 : 2j + 1) e 0 <= 0 <= n, ou seja,
      0 = 0 e 0 <= 0 <= n, ou seja,
      0 <= n, que pela pré-condição é
      V.

Neste caso a inicialização é ainda mais simples!  

CI: 0 <= r e r² <= x.

Basta inicializar r com 0!

/** Devolve a melhor aproximação por defeito de x^½.
    @pre 0 <= x.
    @post 0 <= raizInteiraDe <= x^½ < raizInteiraDe + 1. */
int raizInteiraDe(int const x)
{
    assert(0 <= x);

    // 0 <= x.
    int r = 0;

    // CI: 0 <= r e r² <= x.
    while((r + 1) * (r + 1) <= x) {
        ...
    }

     // CO: 0 <= r <= x^½ < r + 1.

    assert(0 <= r and r * r <= x and x < (r + 1) *(r + 1));

    return r;
}

CI: 0 <= 0 e 0 <= x, que é verdadeira pela pré-condição.

6  Escolha de um progresso

Discutir progressos.  Concluir pela incrementação!

/** Devolve a soma dos primeiros n naturais ímpares.
    @pre 0 <= n.
    @post r = (S j : 0 <= j < n : 2j + 1). */
int somaDosPrimeirosÍmpares(int const n)
{
    assert(0 <= n);

    // 0 <= n.
    int i = 0;
    int r = 0;

    // CI: r = (S j : 0 <= j < i : 2j + 1) e 0 <= i <= n.
    while(i != n) {
        acção
        ++i;
    }

    // CO': r = (S j : 0 <= j < i : 2j + 1) e i = n.
    // que implica CO: r = (S j : 0 <= j < n : 2j +1).
    return r;
}

/** Devolve a melhor aproximação por defeito de x^½.
    @pre 0 <= x.
    @post 0 <= raizInteiraDe <= x^½ < raizInteiraDe + 1. */
int raizInteiraDe(int const x)
{
    assert(0 <= x);

    // 0 <= x.
    int r = 0;

    // CI: 0 <= r e r² <= x.
    while((r + 1) * (r + 1) <= x) {
        acção
        ++r;
    }

     // CO: 0 <= r <= x^½ < r + 1.

    assert(0 <= r and r * r <= x and x < (r + 1) *(r + 1));

    return r;
}

7  Determinação da acção

Esta é uma das fases mais delicadas, logo após a obtenção da condição invariante.  É necessário determinae uma acção que, apesar do progresso, leve à veracidade da condição invariante no final do passo, admitindo-a verdadeira no seu início.

Ou seja, é necessário escolher uma acção acção que apesar do progresso prog garante que a condição invariante se verifica após as duas instruções:

// CI e G.
acção
prog
// CI.

// CI e G: r = (S j : 0 <= j < i : 2j + 1) e 0 <= i <= n e i <> n, ou seja,
//        r = (S j : 0 <= j < i : 2j + 1) e 0 <= i < n.
acção
++i;
// CI: r = (S j : 0 <= j < i : 2j + 1) e 0 <= i <= n.

Usar determinação da pré-condição mais fraca.

// CI e G: r = (S j : 0 <= j < i : 2j + 1) e 0 <= i < n.
acção
// r = (S j : 0 <= j < i + 1 : 2j + 1) e 0 <= i + 1 <= n, ou seja,
// r = (S j : 0 <= j < i + 1 : 2j + 1) e -1 <= i < n.
++i;
// CI: r = (S j : 0 <= j < i : 2j + 1) e 0 <= i <= n.

Que acção escolher?  

Discutir.  Notar que a variável i não precisa de nenhuma alteração.  Centrar atenção na evolução de r.

Exacto!  É necessário acrescentar um termo ao somatório!

r += 2 * i + 1;

A função fica:

/** Devolve a soma dos primeiros n naturais ímpares.
    @pre 0 <= n.
    @post r = (S j : 0 <= j < n : 2j + 1). */
int somaDosPrimeirosÍmpares(int const n)
{
    assert(0 <= n);

    // 0 <= n.
    int i = 0;
    int r = 0;

    // CI: r = (S j : 0 <= j < i : 2j + 1) e 0 <= i <= n.
    while(i != n) {
        r += 2 * i + 1;
        ++i;
    }

    // CO': r = (S j : 0 <= j < i : 2j + 1) e i = n.
    // que implica CO: r = (S j : 0 <= j < n : 2j +1).
    return r;
}

Discutir qual dos dois termos é mais forte!

// CI e G: 0 <= r e r² <= x e (r + 1)² <= x, ou seja,
//        0 <= r e (r + 1)² <= x.
acção
++r;
// CI: 0 <= r e r² <= x.

Mais uma vez determina-se a pré-condição mais fraca:

// CI e G: 0 <= r e r² <= x e (r + 1)² <= x, ou seja,
//        0 <= r e (r + 1)² <= x.
acção
// 0 <= r + 1 e (r + 1)² <= x, ou seja,
// -1 <= r e (r + 1)² <= x.
++r;
// CI: 0 <= r e r² <= x.

Que acção escolher?

Deixá-los discutir!

Exacto: nenhuma!

A função fica:

/** Devolve a melhor aproximação por defeito de x^½.
    @pre 0 <= x.
    @post 0 <= raizInteiraDe <= x^½ < raizInteiraDe + 1. */
int raizInteiraDe(int const x)
{
    assert(0 <= x);

    // 0 <= x.
    int r = 0;

    // CI: 0 <= r e r² <= x.
    while((r + 1) * (r + 1) <= x)
        ++r;

     // CO: 0 <= r <= x^½ < r + 1.

    assert(0 <= r and r * r <= x and x < (r + 1) *(r + 1));

    return r;
}

E pronto!  Depois de algum trabalho, a coisa até ficou simples.

8  E se alguma coisa falhar?

Bom, se as coisas falharem pode ser necessário voltar uns passos atrás na metodologia.

Discutir casos (acção ou inicialização impossível ou demasiado complexa, etc.).

E.g., a condição invariante pode não ser a melhor...
 
Para terminar, será que na soma dos ímpares o ciclo é necessário?

Sejam os números inteiros representados na base 1...
 

*
**
***
****
*****
...

1:

*

*
**

*
*
***

*
*
*
****

Repare-se no que dá a soma dos primeiros quatro ímpares (o quarto ímpar é dado por 2×4 - 1):

****
****
****
****

Logo, enganámo-nos quando pensámos que precisávamos de um ciclo para escrever a função somaDosPrimeirosÍmpares()! A função pode ser simplificada para:

/** Devolve a soma dos primeiros n naturais ímpares.
    @pre 0 <= n.
    @post r = (S j : 0 <= j < n : 2j + 1). */
int somaDosPrimeirosÍmpares(int const n)
{
    assert(0 <= n);

    return n * n;
}

1. Começar, como habitualmente, por especificar o problema.  Isso corresponde a escrever a pré-condição e a condição objectivo do código a desenvolver.
2. Verificar se um ciclo parece uma abordagem apropriada para resolver o problema.  Naturalmente que aqui é preciso algum estudo e, também, alguma intuição.
3. Programação é uma actividade orientada pelos objectivos: deve-se olhar para a condição objectivo e, enfraquecendo-a, obter a condição invariante.
4. Depois procura-se uma guarda que leve ao resultado pretendido quando o ciclo terminar.
5. Determina-se uma inicialização apropriada, que tem de levar à verificação da condição invariante.
6. Determina-se um progresso que leve forçosamente à terminação do ciclo em tempo finito.
7. Determina-se uma acção que, apesar do progresso, leve à veracidade da condição invariante no final do passo, admitindo-a verdadeira no seu início.