Guião da 9ª Aula Teórica

Sumário

Matrizes clássicas do C++:

Noção de matriz como agregado indexável de variáveis do mesmo tipo.
Sintaxe da definição e da inicialização.
Particularidades: dimensão constante, proibidas atribuições, comparações e devoluções, passagens sempre por referência, indexações fora dos limites não verificadas.
Sintomatologia da indexação fora dos limites: alterações em variáveis não envolvidas nos cálculos.

Vectores:

Vantagens face às matrizes.
Operações da classe genérica vector.

Nesta aula vamos falar de agregados. Em particular vamos falar das matrizes clássicas do C++ e dos chamados vectores. Vamos ver que as matrizes clássicas do C++ têm muitos problemas e que os vectores são uma excelente alternativa.

Considerem o problema de ler três inteiros do teclado e de os escrever pela ordem inversa.

Discutir solução.

É evidente que a solução pode ser:

#include <iostream>

using namespace std;
int main()
{
    cout << "Introduza 3 inteiros: ";
    int a, b, c;
    cin >> a >> b >> c;
    cout << c << endl
         << b << endl
         << a << endl;
}

Esta solução é simples e clara. Mas tem um problema: não é generalizável. Se em vez de três passassem a ser 100 inteiros? Será que temos de criar 100 variáveis com nomes diferentes e acrescentá-las às operações de extracção e inserção? Claramente não é prático.

Em todas as linguagens que se prezem há um mecanismo apropriado para resolver este problema: as matrizes.

Note-se que se usa o termo "matriz" como possível tradução do inglês "array". Do mesmo modo se irá usar o termo "vector". As nossas matrizes e vectores não têm senão remota relação com as matrizes da Álgebra!

Uma matriz é um agregado de variáveis do mesmo tipo. Uma matriz é uma variável (quase) como qualquer outra, mas que é constituída na realidade por um determinado número de elementos. Os elementos são conhecidos pelo seu índice, que funciona um pouco como o número da página do elemento.

Em C++ existem as chamadas "matrizes clássicas", que se definem como se segue:

#include <iostream>

using namespace std;
int main()
{
    cout << "Introduza 100 inteiros: ";
    int a, b, c;int m[100];
    cin >> a >> b >> c;
    cout << c << endl
         << b << endl
         << a << endl;
}

Esta instrução constrói uma matriz chamada m com 100 elementos do tipo int. Esta matriz pode ser representada por um diagrama:

Desenhar diagrama "UML" (adaptar diagrama abaixo para 100 elementos).

Repare-se que cada elemento é conhecido por m[i], onde i é o chamado índice do elemento.

Os índices das matrizes em C++ começam sempre em zero!

Assim, a matriz m possui elementos com índices de 0 a 99, ou seja, de 0 à sua dimensão menos um!

A sintaxe da definição de matrizes é:

tipo nome[número_de_elementos];

tipo nome[número_de_elementos] = {lista_de_inicialização};

se se quiser inicializar os seus elementos.

Se não se inicializar uma matriz com elementos de tipos básicos do C++, estes conterão inicialmente lixo. Uma inicialização faz-se indicando os valores iniciais de cada um dos elementos. Por exemplo:

char vogais[5] = {'a', 'e', 'i', 'o', 'u'};

Se faltarem valores iniciais, os elementos por inicializar explicitamente (sempre os últimos) são inicializados implicitamente com zero:

int m[3] = {1, 2};

Assim, uma forma prática de inicializar todos os elementos de uma matriz com zero é escrever:

int m[3] = {};

Quando numa expressão se colocam parênteses rectos após o nome de uma matriz e, dentro destes, uma expressão com valor inteiro, está-se a usar o operador de indexação. É importante perceber que se pode indexar uma matriz com uma expressão qualquer, constante ou não! É aliás isso que permite adaptar de uma forma simples o resto do programa.

O programa como está não funciona. Não existem as variáveis a, b e c. Como fazer a leitura dos 100 valores?

Discutir soluções. Deixar claro que a solução por extensão não nos interessa. Gostaríamos de uma solução por compreensão.

A solução passa obviamente por usar um simples ciclo.

Discutir guarda do ciclo!

#include <iostream>

using namespace std;
int main()
{
    cout << "Introduza 100 inteiros: ";
    int m[100];
    for(int i = 0; i != 100; ++i)
        cin >> m[i];
    cout << c << endl
         << b << endl
         << a << endl;
}

O operador de indexação permitiu-nos fazer a leitura com muita facilidade. Quando a variável i tem o valor 0 é lido o primeiro valor e colocado no primeiro elemento da matriz, quando i tem o valor 1 acontece o mesmo para o segundo valor da matriz, e assim sucessivamente.

O operador de indexação pode ser usado noutros contextos para obter um elemento da matriz que pode ser usado como uma outra variável qualquer:

double m[10];

m[3] = 3.3;
double x = m[3];

Discutir valores iniciais das matrizes.

É importante perceber-se que

Ordinal Índice

primeiro elemento (1º elemento) 0

segundo elemento (2º elemento) 1

n-ésimo elemento (nº elemento) n - 1

Ordinal	Índice
primeiro elemento (1º elemento)	0
segundo elemento (2º elemento)	1
n-ésimo elemento (nº elemento)	n - 1

O mesmo tipo de solução se pode usar agora para fazer a escrita dos valores pela ordem inversa.

Discutir ciclo. Escrever duas alternativas.

#include <iostream>

using namespace std;
int main()
{
    cout << "Introduza 100 inteiros: ";
    int m[100];
    for(int i = 0; i != 100; ++i)
        cin >> m[i];
    for(int i = 99; i != -1; --i)
        cout << m[i] << endl;
    // ou
    for(int i = 100; i != 0; --i)
        cout << m[i - 1] << endl;
}

A primeira solução é preferível, até porque é o exacto simétrico do ciclo directo.

É de notar que os índices envolvidos em ambos os ciclos são:

-1: elemento fictício antes do primeiro, chamar-lhe-emos "elemento inicial";
0: primeiro elemento;
dimensão - 1: último elemento; e
dimensão: elemento fictício depois do último, chamar-lhe-emos "elemento final".

Assim, os ciclos directos começam no primeiro e param quando se chega ao final e os ciclos inversos começam no último e param quando se atinge o inicial.

Suponham agora que se pretendia alterar o número de valores a inverter para 1000. Que alterações se deveria fazer?

Discutir. Concluir que não basta fazer uma substituição de 100 por 1000! Senão o 99 faltaria. Dizer que substituir 100 por 1000 é muito perigoso!

Imaginem que o 100 ocorria no programa como significando, por exemplo, 100 Km/h. Imaginem o resultado de substituir 100 por 1000 se este fosse um programa usado pela brigada de trânsito...

A solução passa por utilizar uma constante:

#include <iostream>

using namespace std;
int main()
{
    int const dimensão = 1000;
    cout << "Introduza " << dimensão << " inteiros: ";
    int m[dimensão];
    for(int i = 0; i != dimensão; ++i)
        cin >> m[i];
    for(int i = dimensão - 1; i != -1; --i)
        cout << m[i] << endl;
    // ou
    for(int i = dimensão; i != 0; --i)
        cout << m[i - 1] << endl;
}

Agora, voltar a alterar o número de valores lidos e invertidos é trivial.

Mas isto leva-nos a uma possível generalização do programa: e se se permitisse ao utilizador especificar o número de valores e ler e inverter? Que tal

#include <iostream>

using namespace std;
int main()
{
    cout << "Introduza o número de valores a ler e inverter: ";
    int dimensão;
    cin >> dimensão;
    cout << "Introduza " << dimensão << " inteiros: ";     int m[dimensão];
    for(int i = 0; i != dimensão; ++i)
        cin >> m[i];
    for(int i = dimensão - 1; i != -1; --i)
        cout << m[i] << endl;
    // ou
    for(int i = dimensão; i != 0; --i)
        cout << m[i - 1] << endl;
}

Acontece que isto não é possível: o compilador tem de saber a dimensão exacta das matrizes construídas!

Mais, uma vez estabelecida, a dimensão das matrizes é imutável!

Repare-se que não se resolve o problema com truques:

#include <iostream>

using namespace std;
int main()
{
    cout << "Introduza o número de valores a ler e inverter: ";
    int n;
    cin >> n;
    int const dimensão = n;
    cout << "Introduza " << dimensão << " inteiros: ";     int m[dimensão];
    for(int i = 0; i != dimensão; ++i)
        cin >> m[i];
    for(int i = dimensão - 1; i != -1; --i)
        cout << m[i] << endl;
    // ou
    for(int i = dimensão; i != 0; --i)
        cout << m[i - 1] << endl;
}

Explicar que tem de ser uma constante com valor conhecido pelo compilador!

Este é um problema grave das matrizes: a sua dimensão tem de ser conhecida durante a compilação e não pode variar. Uma matriz com 1000 elementos será sempre uma matriz com 1000 elementos.

Estes e outros problemas com estas chamadas matrizes clássicas do C++ levar-nos-ão a usar uma alternativa simpática às matrizes: os vectores. A ver no final da aula...

Assim sendo, não temos outro remédio, para já, senão voltar ao código original...

#include <iostream>

using namespace std;
int main()
{
    int const dimensão = 1000;
    cout << "Introduza " << dimensão << " inteiros: ";
    int m[dimensão];
    for(int i = 0; i != dimensão; ++i)
        cin >> m[i];
    for(int i = dimensão - 1; i != -1; --i)
        cout << m[i] << endl;
    // ou
    for(int i = dimensão; i != 0; --i)
        cout << m[i - 1] << endl;
}

Podemos agora tentar melhorar o programa de modo a usar um pouco de modularização: é sempre boa ideia...

Precisamos de dois módulos na forma de rotinas: uma que permita obter os valores extraídos do teclado, e outra que os escreva por ordem inversa. A segunda chamar-se-á escreveInvertida() e é naturalmente um procedimento:

#include <iostream>

using namespace std;
/** Escreve no ecrã os elementos da matriz passada como argumento
    começando no último.*/ void escreveInvertida(...)
{
    ...
}
int main()
{
    int const dimensão = 1000;
    cout << "Introduza " << dimensão << " inteiros: ";
    int m[dimensão];
    for(int i = 0; i != dimensão; ++i)
        cin >> m[i];
    for(int i = dimensão - 1; i != -1; --i)
        cout << m[i] << endl;
    // ou
    for(int i = dimensão; i != 0; --i)
        cout << m[i - 1] << endl;
}

A primeira não é tão evidente. Se for uma função, devolverá a matriz lida, pelo que se poderá chamar matrizLida(). Se for um procedimento, recebe por referência a matriz onde deve colocar os valor lidos e deve-se chamar lêPara().

Na realidade, porém, o C++ não nos deixa alternativa: não é possível devolver matrizes em C++.

Neste caso nem é problemático, pois a rotina de devolver a matriz teria sempre duas funções: ler a matriz e devolvê-la. Ou a interpretávamos como uma função com efeitos laterais ou como um procedimento que devolve um valor. Ambas má ideia...

Já começamos a ver que as chamadas matrizes clássicas têm uns quantos problemas... No fim desta aula veremos os chamados vectores, que não têm nenhum dos problemas das matrizes...

#include <iostream>

using namespace std;
/** Lê do teclado valores inteiros que coloca por ordem nos elementos da
    matriz passada como argumento.*/void lêPara(...)
{
    ...
}
/** Escreve no ecrã os elementos da matriz passada como argumento
    começando no último.*/ void escreveInvertida(...)
{
    ...
}
int main()
{
    int const dimensão = 1000;
    cout << "Introduza " << dimensão << " inteiros: ";
    int m[dimensão];
    for(int i = 0; i != dimensão; ++i)
        cin >> m[i];
    for(int i = dimensão - 1; i != -1; --i)
        cout << m[i] << endl;
    // ou
    for(int i = dimensão; i != 0; --i)
        cout << m[i - 1] << endl;
}

Que parâmetros deverão ter os procedimentos? O primeiro, para leitura, deverá receber a matriz por referência, de modo a alterar a matriz passada por referência. O segundo deverá receber a matriz por valor. Ou seja:

#include <iostream>

using namespace std;
/** Lê do teclado valores inteiros que coloca por ordem nos elementos da
    matriz passada como argumento.   @pre cin.good() e cin permite extracção de dimensão inteiros sucessivos.
    @post ¬cin.good() ou cin já não contém os primeiros dimensão inteiros que
          continha inicialmente e a matriz m contém-nos pela mesma ordem.*/ void lêPara(int m[dimensão])
{
    ...
}
/** Escreve no ecrã os elementos da matriz passada como argumento
    começando no último.    @pre cout.good() e podem-se inserir os dimensão inteiros da matriz m no canal cout.   @post ¬cout.good() ou cout sofreu inserções dos dimensão elementos da matriz
           m pela sua ordem inversa.*/ void escreveInvertida(int m[dimensão])
{
    ...
}
int main()
{
    int const dimensão = 1000;
    cout << "Introduza " << dimensão << " inteiros: ";
    int m[dimensão];
    for(int i = 0; i != dimensão; ++i)
        cin >> m[i];
    for(int i = dimensão - 1; i != -1; --i)
        cout << m[i] << endl;
    // ou
    for(int i = dimensão; i != 0; --i)
        cout << m[i - 1] << endl;
}

Há aqui dois problemas. O primeiro é que não se está a distinguir entre passagem de matrizes por valor e por referência. Pois. O problema é que em C++ as matrizes são sempre passadas por referência!

Dizer que é uma mentirinha inocente, que será desmentida no segundo semestre... Mencionar en passant ponteiros, para quem queira perceber melhor o assunto ter pelo menos uma referência.

Isto põe-nos um problema adicional. Se todas as matrizes são passadas por referência, como podemos deixar claro que o procedimento escreveInvertida() não é suposto alterar a matriz passada como argumento? A solução passa por dizer que a matriz passada por referência é uma matriz de elementos constantes!

#include <iostream>

using namespace std;
/** Lê do teclado valores inteiros que coloca por ordem nos elementos da
    matriz passada como argumento.   @pre cin.good() e cin permite extracção de dimensão inteiros sucessivos.
    @post ¬cin.good() ou cin já não contém os primeiros dimensão inteiros que
          continha inicialmente e a matriz m contém-nos pela mesma ordem.*/ void lêPara(int m[dimensão])
{
    ...
}
/** Escreve no ecrã os elementos da matriz passada como argumento
    começando no último.    @pre cout.good() e podem-se inserir os dimensão inteiros da matriz m no canal cout.   @post ¬cout.good() ou cout sofreu inserções dos dimensão elementos da matriz
           m pela sua ordem inversa.*/ void escreveInvertida(int const m[dimensão])
{
    ...
}
int main()
{
    int const dimensão = 1000;
    cout << "Introduza " << dimensão << " inteiros: ";
    int m[dimensão];
    for(int i = 0; i != dimensão; ++i)
        cin >> m[i];
    for(int i = dimensão - 1; i != -1; --i)
        cout << m[i] << endl;
    // ou
    for(int i = dimensão; i != 0; --i)
        cout << m[i - 1] << endl;
}

Sobrou-nos um outro problema: a constante dimensão não é conhecida fora da função main(), e portanto não pode ser utilizada nos cabeçalhos dos procedimentos... Uma possível solução é tornar a constante global:

#include <iostream>

using namespace std;
int const dimensão = 1000;
/** Lê do teclado valores inteiros que coloca por ordem nos elementos da
    matriz passada como argumento.   @pre cin.good() e cin permite extracção de dimensão inteiros sucessivos.
    @post ¬cin.good() ou cin já não contém os primeiros dimensão inteiros que
          continha inicialmente e a matriz m contém-nos pela mesma ordem.*/ void lêPara(int m[dimensão])
{
    ...
}
/** Escreve no ecrã os elementos da matriz passada como argumento
    começando no último.    @pre cout.good() e podem-se inserir os dimensão inteiros da matriz m no canal cout.   @post ¬cout.good() ou cout sofreu inserções dos dimensão elementos da matriz
           m pela sua ordem inversa.*/ void escreveInvertida(int const m[dimensão])
{
    ...
}
int main()
{
    cout << "Introduza " << dimensão << " inteiros: ";
    int m[dimensão];
    for(int i = 0; i != dimensão; ++i)
        cin >> m[i];
    for(int i = dimensão - 1; i != -1; --i)
        cout << m[i] << endl;
    // ou
    for(int i = dimensão; i != 0; --i)
        cout << m[i - 1] << endl;
}

O problema agora tem mais uma vez a ver com a particularidade das matrizes do C++: quando uma matriz ocorre como parâmetro de uma rotina, a sua dimensão é simplesmente ignorada!

Dizer en passant que isto tem mais uma vez a ver com ponteiros.

Bolas! Então tudo fica na mesma se se omitir a dimensão das matrizes usadas como parâmetros:

#include <iostream>

using namespace std;
int const dimensão = 1000;
/** Lê do teclado valores inteiros que coloca por ordem nos elementos da
    matriz passada como argumento.   @pre cin.good() e cin permite extracção de dimensão inteiros sucessivos.
    @post ¬cin.good() ou cin já não contém os primeiros dimensão inteiros que
          continha inicialmente e a matriz m contém-nos pela mesma ordem.*/ void lêPara(int m[])
{
    ...
}
/** Escreve no ecrã os elementos da matriz passada como argumento
    começando no último.    @pre cout.good() e podem-se inserir os dimensão inteiros da matriz m no canal cout.   @post ¬cout.good() ou cout sofreu inserções dos dimensão elementos da matriz
           m pela sua ordem inversa.*/ void escreveInvertida(int const m[])
{
    ...
}
int main()
{
    cout << "Introduza " << dimensão << " inteiros: ";
    int m[dimensão];
    for(int i = 0; i != dimensão; ++i)
        cin >> m[i];
    for(int i = dimensão - 1; i != -1; --i)
        cout << m[i] << endl;
    // ou
    for(int i = dimensão; i != 0; --i)
        cout << m[i - 1] << endl;
}

Falta, claro está, completar os corpos dos procedimentos e usá-los na função main():

#include <iostream>

using namespace std;
int const dimensão = 1000;
/** Lê do teclado valores inteiros que coloca por ordem nos elementos da
    matriz passada como argumento.   @pre cin.good() e cin permite extracção de dimensão inteiros sucessivos.
    @post ¬cin.good() ou cin já não contém os primeiros dimensão inteiros que
          continha inicialmente e a matriz m contém-nos pela mesma ordem.*/ void lêPara(int m[])
{
    assert(cin.good());
    for(int i = 0; i != dimensão; ++i)
        cin >> m[i];
}
/** Escreve no ecrã os elementos da matriz passada como argumento
    começando no último.    @pre cout.good() e podem-se inserir os dimensão inteiros da matriz m no canal cout.   @post ¬cout.good() ou cout sofreu inserções dos dimensão elementos da matriz
           m pela sua ordem inversa.*/ void escreveInvertida(int const m[])
{
    assert(cout.good());
    for(int i = dimensão - 1; i != -1; --i)
        cout << m[i] << endl;
    // ou
    for(int i = dimensão; i != 0; --i)
        cout << m[i - 1] << endl;
}
int main()
{
    cout << "Introduza " << dimensão << " inteiros: ";
    int m[dimensão];
    lêPara(m);
    escreveInvertida(m);
}

Repare-se que nesta solução continua a precisar-se da constante global. Além disso, os dois procedimentos estão condenados a trabalhar com matrizes com exactamente o número de elementos dados pela constante dimensão.

Será que podemos flexibilizar os procedimentos para funcionarem com matrizes de dimensões arbitrárias?

Discutir. Concluir que basta passar a dimensão como argumento adicional.

Ou seja:

#include <iostream>

using namespace std;
/** Lê do teclado valores inteiros que coloca por ordem nos elementos da
    matriz passada como argumento.   @pre 0 <= dimensão e dimensão <= dim(m) e cin.good() e cin
       permite extracção de dimensão inteiros sucessivos.
    @post ¬cin.good() ou cin já não contém os primeiros dimensão inteiros que
          continha inicialmente e a matriz m contém-nos pela mesma ordem.*/ void lêPara(int m[], int const dimensão)
{     assert(cin.good() and 0 <= dimensão);
    for(int i = 0; i != dimensão; ++i)
        cin >> m[i];
}
/** Escreve no ecrã os elementos da matriz passada como argumento
    começando no último.    @pre 0 <= dimensão e dimensão <= dim(m) e cout.good() e podem-se
          inserir os dimensão inteiros da matriz m no canal cout.   @post ¬cout.good() ou cout sofreu inserções dos dimensão elementos da matriz
           m pela sua ordem inversa.*/ void escreveInvertida(int const m[], int const dimensão)
{
    assert(cout.good() and 0 <= dimensão);
    for(int i = dimensão - 1; i != -1; --i)
        cout << m[i] << endl;
    // ou
    for(int i = dimensão; i != 0; --i)
        cout << m[i - 1] << endl;
}
int main()
{
    int const dimensão = 1000;
    cout << "Introduza " << dimensão << " inteiros: ";
    int m[dimensão];
    lêPara(m, dimensão);
    escreveInvertida(m, dimensão);
}

Repare-se que agora os procedimentos são genéricos: funcionam tão bem para matrizes com 1000 elementos como para matrizes com 3 ou 3000000 elementos. Aliás, mais do que isso, a dimensão passada como argumento a estes procedimentos não precisa de ser igual à dimensão real das matrizes: pode ser menor. Claro está que não pode ser maior, pois de outra forma tentar-se-ia aceder a elementos inexistentes da matriz.

Isto leva-nos a uma outra característica indesejável das matrizes: as indexações de matrizes não são verificadas! Que acontece quando se indexa uma matriz fora dos seus limites?

Suponha-se o seguinte código:

int a = 0;
int m[3];
int b = 0;

m[-1] = 1;
m[3] = 2;
cout << a << ' ' << b << endl;

Que acontece quando este código é executado? Uma de quatro coisas:

O programa aborta com uma mensagem de erro do tipo "Segmentation fault: core dumped".
O programa escreve: 2 1.
O programa escreve: 1 2.
Outro comportamento qualquer, incluindo o programa parecer funcionar sem problemas.

Se tivermos sorte o programa aborta! É sorte porque se percebe imediatamente que tem um erro. Com azar dá qualquer dos outros três resultados, sendo o pior o último.

Porquê? É simples. As variáveis a, m e b são provavelmente organizadas na memória como se segue:

a

m[2]

m[1]

m[0]

b

Logo, escrever m[3] acaba por ser o mesmo que escrever a, e escrever m[-1] dá no mesmo que escrever b! Contra-intuitivo e desagradável.

Conclusão: cuidado com as indexações!

Para concluir o nosso périplo pelos problemas das matrizes, falta apenas dizer que estas têm duas restrições adicionais: não se podem atribuir nem comparar matrizes! Ou seja, não é possível escrever o código:

double valores1[2] = {1.1, 2.2};
double valores2[2] = {3.3, 4.4};

if(valores 1 != valores2)
valores1 = valores2;

Finalmente, falta abordar a questão das matrizes multi-dimensionais. As matrizes clássicas do C++ são unidimensionais. Não é possível definir matrizes multi-dimensionais: é conceito que não existe em C++!

Mas é possível definir matrizes de matrizes, o que acaba por ter o mesmo efeito prático. Por exemplo:

double matriz[2][3];

define uma matriz com três elementos, cada um dos quais é uma matriz com dois elementos do tipo double. A interpretação é:

double (matriz[2])[3];

Desenhar pequeno diagrama simplificado.

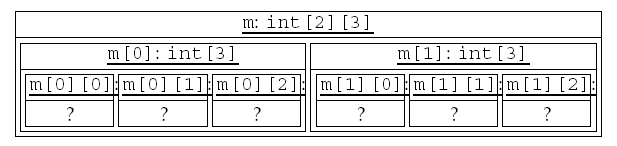
Que sucede se se fizer a atribuição

matriz[1][0] = 12.0;

Discutir e explicar.

Alinhar os defeitos das matrizes:

Têm dimensão fixa;
a dimensão é especificada em tempo de compilação;
a inicialização não permite especificar grandes quantidades de valores;
são sempre passadas por referência (mentirita...);
a sua dimensão é ignorada nos parâmetros de rotinas;
não há forma de lhes perguntar a sua dimensão (pelo menos óbvia);
não podem ser devolvidas;
não podem ser atribuídas;
não podem ser comparadas; e
indexações inválidas não são verificadas.

Começámos esta aula dizendo que os vectores definidos pela biblioteca padrão do C++ são uma boa alternativa às matrizes. De facto, assim é.

Para fazer uso dos vectores é necessário incluir o ficheiro de interface vector, ou seja, tem de se colocar no início do programa a seguinte linha:

#include <vector>

Este ficheiro contém a definição de uma classe genérica chamada vector. A noção de classe será vista a partir das próximas aulas. Para já é suficiente dizer que classes são tipos definidos pelo utilizador, ou seja, tipos adicionados aos tipos básicos do C++.

Ou seja, o ficheiro contém a definição de um tipo genérico chamado vector. Porquê "tipo genérico" e não apenas tipo? Porque um tipo genérico representa um conjunto parametrizável de tipos.

No caso do tipo modelo vector, há apenas um parâmetro a ser especificado: é o parâmetro onde se diz qual o tipo dos itens do vector! Esse tipo coloca-se entre parênteses agudos após o nome do tipo modelo:

vector<double> v;

Esta instrução define uma variável v que é um vector de itens do tipo double. Como não se especificou qualquer dimensão para o vector, terá dimensão nula. Isso não é problemático porque os vectores podem mudar de dimensão sempre que necessário.

É possível indicar uma dimensão inicial para o vector:

vector<double> v(10);

A dimensão inicial não precisa de ser conhecida do compilador!

Também é possível dizer qual o valor com que todos os itens do vector devem ser inicializados.

vector<double> v(10, 13.0);

Infelizmente não é possível inicializar os itens com valores distintos, com se faz no caso das matrizes, pelo menos de uma forma óbvia.

Esperam-se evoluções da linguagem nesse sentido!

Ao contrário do que acontece com as matrizes, os vectores:

Têm dimensão variável;
a dimensão não precisa de ser especificada em tempo de compilação;
a inicialização permite especificar grandes quantidades de valores;
a inicialização para poucos valores é pior;
podem ser passados por valor ou referência;
a sua dimensão não é ignorada nos parâmetros de rotinas;
pode-se-lhes perguntar a sua dimensão;
podem ser devolvidos;
podem ser atribuídos;
podem ser comparados; e
indexações inválidas também não são verificadas.

Tal como no caso das matrizes, os índices não são verificados.

Os vectores têm uma vantagem adicional: sabem a sua dimensão. Por exemplo:

vector<double> v(10, 13.0);
cout << v.size() << endl;

Para saber a dimensão de um vector usa-se a operação size(). Uma operação é como que uma rotina que se aplica a uma determinada variável. O assunto será clarificado nas próximas aulas, bastando para já dizer que a sintaxe de invocação de uma operação é:

variável.operação(lista_de_argumentos)

A operação size() devolve um inteiro sem sinal. Mas o tipo exacto não é especificado. Pode ser um dos três tipos aritméticos inteiros sem sinal do C++:

unsigned short int
unsigned int
unsigned long int

Existe um sinónimo desse tipo disponível, que nos permite escrever código sem saber exactamente que tipo é esse:

vector<double>::size_type

é um sinónimo do tipo que deve ser usado para guardar a dimensão de vectores de double.

Torna-se agora possível traduzir o código desenvolvido de modo a usar vectores.

Discutir alterações assinaladas! Explicar porque deixa de haver a primeira alternativa do ciclo inverso.

#include <iostream>
#include <vector>

using namespace std;
/** Lê do teclado valores inteiros que coloca por ordem nos itens do
    vector passado como argumento.   @pre cin.good() e cin permite extracção de m.size() inteiros sucessivos.
    @post ¬cin.good() ou cin já não contém os primeiros m.size() inteiros que
          continha inicialmente e o vector m contém-nos pela mesma ordem.*/ void lêPara(vector<int>& m)
{
    assert(cin.good());
    for(vector<int>::size_type i = 0; i != m.size(); ++i)
        cin >> m[i];
}
/** Escreve no ecrã os itens do vector passado como argumento
    começando no último.    @pre cout.good() e podem-se inserir os m.size() inteiros do vector m no
           canal cout.   @post ¬cout.good() ou cout sofreu inserções dos m.size() itens do vector
           m pela sua ordem inversa.*/ void escreveInvertido(vector<int> m)
{
    assert(cout.good());
    for(vector<int>::size_type i = m.size() - 1; i != -1; --i)
        cout << m[i] << endl;
    // ou
    for(vector<int>::size_type i = m.size(); i != 0; --i)
        cout << m[i - 1] << endl;
}
int main()
{
    int const dimensão = 1000;
    cout << "Introduza " << dimensão << " inteiros: ";
    vector<int> m(dimensão);
    lêPara(m);
    escreveInvertido(m);
}

Lembram-se porque se decidiu usar um procedimento para ler o valores? Simplesmente porque não se podiam devolver matrizes! Mas vectores podem!

Discutir solução com função:

#include <iostream>
#include <vector>

using namespace std;
vector<int> vectorLido(int dimensão)
{
    assert(cin.good());
    vector<int> m(dimensão);
    for(vector<int>::size_type i = 0; i != m.size(); ++i)
        cin >> m[i];
    return m;
}
/** Escreve no ecrã os itens do vector passado como argumento
    começando no último.    @pre cout.good() e podem-se inserir os m.size() inteiros do vector m no
           canal cout.   @post ¬cout.good() ou cout sofreu inserções dos m.size() itens do vector
           m pela sua ordem inversa.*/ void escreveInvertido(vector<int> m)
{
    assert(cout.good());
    for(vector<int>::size_type i = m.size(); i != 0; --i)
        cout << m[i - 1] << endl;
}
int main()
{
    int const dimensão = 1000;
    cout << "Introduza " << dimensão << " inteiros: ";
    vector<int> m = vectorLido(dimensão);
    escreveInvertido(m);
}

Os vectores têm duas operações simétricas, chamadas push_back() e pop_back(). A primeira recebe como argumento o valor de um novo item que é acrescentado ao vector no seu final. A segunda remove o item final de um vector. Recorrendo à primeira, pode-se escrever a função de leitura de uma forma diferente:

#include <iostream>
#include <vector>

using namespace std;
vector<int> vectorLido(int dimensão)
{
    assert(cin.good());
    vector<int> m;
    for(int i = 0; i != dimensão; ++i) {
        int valor;
        cin >> valor;
        m.push_back(valor);
    }
    return m;
}
/** Escreve no ecrã os itens do vector passado como argumento
    começando no último.    @pre cout.good() e podem-se inserir os m.size() inteiros do vector m no
           canal cout.   @post ¬cout.good() ou cout sofreu inserções dos m.size() itens do vector
           m pela sua ordem inversa.*/ void escreveInvertido(vector<int> m)
{
    assert(cout.good());
    for(vector<int>::size_type i = m.size(); i != 0; --i)
        cout << m[i - 1] << endl;
}
int main()
{
    int const dimensão = 1000;
    cout << "Introduza " << dimensão << " inteiros: ";
    vector<int> m = vectorLido(dimensão);
    escreveInvertido(m);
}

Discutir desvantagem: mais lento, menos claro.

Discutir cópias: quer na devolução quer na passagem por valor. Regressar ao procedimento, argumentando de novo contra as rotinas dois em um!

#include <iostream>
#include <vector>

using namespace std;
/** Lê do teclado valores inteiros que coloca por ordem nos itens do
    vector passado como argumento.   @pre cin.good() e cin permite extracção de m.size() inteiros sucessivos.
    @post ¬cin.good() ou cin já não contém os primeiros m.size() inteiros que
          continha inicialmente e o vector m contém-nos pela mesma ordem.*/ void lêPara(vector<int>& m)
{
    assert(cin.good());
    for(vector<int>::size_type i = 0; i != m.size(); ++i)
        cin >> m[i];
}
/** Escreve no ecrã os itens do vector passado como argumento
    começando no último.    @pre cout.good() e podem-se inserir os m.size() inteiros do vector m no
           canal cout.   @post ¬cout.good() ou cout sofreu inserções dos m.size() itens do vector
           m pela sua ordem inversa.*/ void escreveInvertido(vector<int> m)
{
    assert(cout.good());
    for(vector<int>::size_type i = m.size(); i != 0; --i)
        cout << m[i - 1] << endl;
}
int main()
{
    int const dimensão = 1000;
    cout << "Introduza " << dimensão << " inteiros: ";
    vector<int> m(dimensão);
    lêPara(m);
    escreveInvertido(m);
}

Como evitar cópias no caso das passagens por valor? Uma possibilidade é passar a usar passagens por referência. Mas se se usar passagem por referência está-se a dar uma mensagem clara ao compilador: o procedimento pode alterar o vector! Mas isso não é verdade! Como resolver o problema? Dizendo que, apesar de a passagem ser feita por referência, o procedimento está proibido de alterar o vector:

#include <iostream>
#include <vector>

using namespace std;
/** Lê do teclado valores inteiros que coloca por ordem nos itens do
    vector passado como argumento.   @pre cin.good() e cin permite extracção de m.size() inteiros sucessivos.
    @post ¬cin.good() ou cin já não contém os primeiros m.size() inteiros que
          continha inicialmente e o vector m contém-nos pela mesma ordem.*/ void lêPara(vector<int>& m)
{
    assert(cin.good());
    for(vector<int>::size_type i = 0; i != m.size(); ++i)
        cin >> m[i];
}
/** Escreve no ecrã os itens do vector passado como argumento
    começando no último.    @pre cout.good() e podem-se inserir os m.size() inteiros do vector m no
           canal cout.   @post ¬cout.good() ou cout sofreu inserções dos m.size() itens do vector
           m pela sua ordem inversa.*/ void escreveInvertido(vector<int> const& m)
{
    assert(cout.good());
    for(vector<int>::size_type i = m.size(); i != 0; --i)
        cout << m[i - 1] << endl;
}
int main()
{
    int const dimensão = 1000;
    cout << "Introduza " << dimensão << " inteiros: ";
    vector<int> m(dimensão);
    lêPara(m);
    escreveInvertido(m);
}

Explicar bem a noção de um sinónimo restritivo!

Repare-se que se pode generalizar este programa tirando partido do facto de que a dimensão dos vectores é totalmente livre: pode ser o próprio utilizador a indicar qual o número de valores a ler e inverter. Além disso, é melhor ideia usar um nome para o vector que seja indicativo do que é guardado:

#include <iostream>
#include <vector>

using namespace std;
/** Lê do teclado valores inteiros que coloca por ordem nos itens do
    vector de valores passado como argumento.   @pre cin.good() e cin permite extracção de m.size() inteiros sucessivos.
    @post ¬cin.good() ou cin já não contém os primeiros m.size() inteiros que
          continha inicialmente e o vector m contém-nos pela mesma ordem.*/ void lêPara(vector<int>& valores)
{
    assert(cin.good());
    for(vector<int>::size_type i = 0; i != valores.size(); ++i)
        cin >> valores[i];
}
/** Escreve no ecrã os valores passados como argumento, começando no último.    @pre cout.good() e podem-se inserir os m.size() inteiros do vector m no
           canal cout.   @post ¬cout.good() ou cout sofreu inserções dos m.size() itens do vector
           m pela sua ordem inversa.*/ void escreveInvertido(vector<int> const& valores)
{
    assert(cout.good());
    for(vector<int>::size_type i = valores.size(); i != 0; --i)
        cout << valores[i - 1] << endl;
}
int main()
{
    cout << "Quantos valores quer que sejam lidos e invertidos? ";
    int dimensão;
    cin >> dimensão;
    cout << "Introduza " << dimensão << " inteiros: ";
    vector<int> valores(dimensão);
    lêPara(valores);
    escreveInvertido(valores);
}

Para terminar, falta referir uma operação muito útil dos vectores, que permite alterar a sua dimensão:

vector<int> v(5, 1);
v.resize(8);
v.resize(9, 2);
v.resize(2);

Discutir.