Guião da 10ª Aula Teórica

Sumário

1. Necessidade de TAD: acrescentando tipos ao C++.
2. Sintaxe da definição de classes C++.
3. Sintaxe da definição de variáveis de uma classe C++: as instâncias e a instanciação.
4. Variáveis e constantes membro: atributos.
5. Acesso a variáveis membro de uma classe C++: operador de selecção de membro.
6. Rotinas membro: operações e métodos.  Declaração vs. definição.  A construção TAD::.
7. Acesso a membros de uma classe C++: a variável implícita.
8. Construtores: sintaxe e utilização.
9. Parâmetros com valores por omissão de novo.
10. Categorias e políticas de acesso: membros públicos vs. membros privados.
11. Princípio do encapsulamento: aplicação aos TAD.
12. Noção de condição invariante de classe (CIC): regras e vantagens.
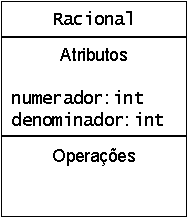
13. Exemplos com o TAD Racional, para concretização do conceito de número racional.

Relembrar exercício da soma de fracções na Aula 4.  Escrever no quadro o programa desenvolvido, deixando espaço para poder passar a usar o novo tipo:

#include <iostream>
#include <cassert>

using namespace std;

/** Devolve o máximo divisor comum dos inteiros passados como argumento.
    @pre m <> 0 ou n <> 0.
    @post mdc = mdc(m, n). */
int mdc(int const m, int const n) 
{
    assert(m != 0 or n != 0);
    ...
}

Deixar aqui espaço para a classe e respectivos construtores!  Na classe deixar espaço para as declarações das operações!

/** Reduz a fracção recebida como argumento.
    @pre denominador <> 0 e numerador = n e denominador = d.
    @post denominador <> 0 e mdc(numerador, denominador) = 1 e
        numerador/denominador = n/d. */
void reduzFracção(int& numerador, int& denominador)
{
    assert(denominador != 0);

    int k = mdc(numerador, denominador);

    numerador /= k;
    denominador /= k;

    assert(denominador != 0 and mdc(numerador, denominador) == 1);
}

/** Lê do teclado uma fracção, na forma de dois inteiros sucessivos.
    @pre numerador = n e denominador = d.
    @post Se cin.good() e cin tem dois inteiros n' e d' disponíveis para
        leitura, com d' <> 0, então
        0 < denominador e mdc(numerador, denominador) = 1 e
        numerador/denominador = n'/d' e cin.good(),
        senão numerador = n e denominador = d e ¬cin.good(). */
void lêFracção(int& numerador, int& denominador)
{
    int n, d;

    cin >> n >> d;
    if(cin.good())
        if(d == 0)
            cin.setstate(ios_base::failbit);
        else {
            if(d < 0) {
                numerador = -n;
                denominador = -d;
            } else {
                numerador = n;
                denominador = d;
            }
            reduzFracção(numerador, denominador);

            assert(0 < denominador and mdc(numerador, denominador) == 1 and
                   numerador * d == n * denominador and cin.good());

            return;
        }

    assert(not cin.good());
}

/** Soma duas fracções.
    @pre denominador1 <> 0 e denominador2 <> 0.
    @post numerador/denominador = numerador1/denominador1 +
                                 numerador2/denominador2 e
           denominador <> 0 e mdc(numerador, denominador) = 1. */
void somaFracção(int& numerador, int& denominador, 
                 int const numerador1, int const denominador1,
                 int const numerador2, int const denominador2)
{
    assert(denominador1 != 0 and denominador2 != 0);

    numerador = numerador1 * denominador2 + numerador2 * denominador1;
    denominador = denominador1 * denominador2;

    reduzFracção(numerador, denominador);

    assert(denominador != 0 and mdc(numerador, denominador) == 1);
}

/** Escreve uma fracção no ecrã no formato usual.
    @pre V.
    @post ¬cout.good() ou cout contém n/d (ou simplesmente
          n, se d = 1) em que n e d são os valores de numerador e denominador. */
void escreveFracção(int const numerador, int const denominador)
{
    cout << numerador;
    if(denominador != 1)
        cout << '/' << denominador;
}

int main()
{
    // Ler fracções:
    cout << "Introduza duas fracções (numerador denominador): ";
    int n1, d1, n2, d2;
    lêFracção(n1, d1);
    lêFracção(n2, d2);

    if(not cin) {
        cout << "Opps!  A leitura das fracções falhou!" << endl;
        return 1;
    }

    // Calcular fracção soma reduzida:
    int n, d;
    somaFracção(n, d, n1, d1, n2, d2);

    // Escrever resultado:
    cout << "A soma de ";
    escreveFracção(n1, d1);
    cout << " com ";
    escreveFracção(n2, d2);
    cout << " é ";
    escreveFracção(n, d);
    cout << '.' << endl;
} 

Observações:

1. O programa original só funcionava para fracções com numerador e denominador positivo, por causa da função mdc().  É possível relaxar esta restrição reescrevendo a função mdc().  Isso está feito nas folhas teóricas.  A partir daqui assume-se que a função usada não tem restrições.
   
2. Usamos dois inteiros para cada fracção e por isso não podemos usar funções para a rotina somaFracção(), que só devolve um valor.

Este programa deixa-nos um pouco desiludidos por um simples facto: cada fracção é representada por dois inteiros e, por isso, o código torna-se complexo e difícil de perceber.

Gostaríamos escrever o programa como o escreveríamos se o seu objectivo fosse ler e somar inteiros, e não fracções.

Sendo as fracções representações dos números racionais, pretendíamos escrever o programa como se segue:

...

int main()
{
    cout << "Introduza duas fracções (numerador denominador): ";
    Racional r1, r2;
    cin >> r1 >> r2;

    if(not cin) {
        cout << "Opps!  A leitura dos racionais falhou!" << endl;
        return 1;
    }

    Racional r = r1 + r2;

    cout << "A soma de " << r1 << " com " << r2 << " é "
         << r << '.' << endl;
}

Como representar cada racional com uma variável apenas?  

Temos de definir um tipo novo que se comporte como qualquer outro tipo em C++.  Precisamos de de um tipo abstracto de dados (TAD) ou tipo de primeira categoria.  Um TAD ou tipo de primeira categoria é um tipo definido pelo programador que se comporta como os tipos básicos, servindo para definir variáveis que guardam valores sobre os quais se pode operar.  O C++ proporciona uma ferramenta, as classes, que nos permite definir tipos de primeira categoria.  Assim, é possível definir um tipo para representar números racionais (na forma de uma fracção), como se segue:

...

/** Representa números racionais. */
class Racional {
  public: // Isto é magia.
    int numerador;
    int denominador;
};

...

Colocar isto depois da função mdc(), no espaço!  Deixar espaço dentro da classe para as operações!

Chamar atenção para ; final!

Note-se que os termos enganam.  No segundo semestre vamos aprender a trabalhar com classes propriamente ditas, que se implementam também usando as classes do C++!  Isso vai levar inevitavelmente a alguma confusão de nomenclatura.  

Assim:

• TAD: tipo definido pelo utilizador que se comporta como qualquer tipo básico da linguagem.
• Classe propriamente dita: conceito mais complexo a estudar no 2º semestre.
• Classe C++: a ferramenta da linguagem que permite implementar quer TAD  quer classes propriamente ditas.

Ou seja, quando no primeiro semestre nos referirmos a classe, estamos a referir-nos quase sempre a um tipo de primeira categoria.

Desenhar diagrama UML.  Deixar espaço para operações:

Se conveniente, usar como atributos n e d, dizendo que o fazemos para poupar tinta.  Mas dizer-lhes quais os nomes correctos e descritivos!

Também podem existir constantes membro.  As variáveis e as constantes membro de uma classe recebem o nome de atributos do TAD.

Cada variável de um determinado TAD tem as suas próprias versões dos atributos!

O TAD pode ser usado como se segue:

Racional r1, r2;

r1.numerador = 6;
r1.denominador = 9;

r2.numerador = 7;
r2.denominador = 3;

Desenhar diagramas UML!

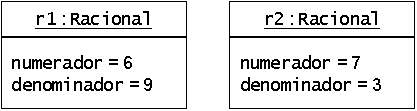
ou

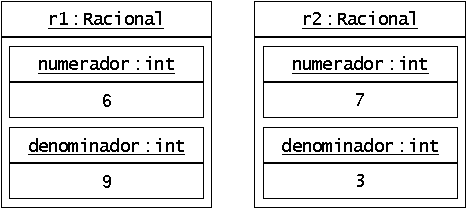
Às variáveis de um TAD também é comum chamar-se objectos.

Acede-se aos membros de uma variável de um TAD usando o operador de selecção de membro .:

variável.membro

...

/** Devolve a Ssoma duas fracções de dois racionais.
    @pre r1.denominador1 <> 0 e r2.denominador2 <> 0.
    @post numerador/denominador somaDe = numerador1/denominador1 r1 + numerador2/denominador2 r2 e
           somaDe.denominador <> 0 e mdc(somaDe.numerador, somaDe.denominador) = 1. */
voidRacional somaDeFracção(int& numerador, int& denominador,
                         int const numerador1, int const denominador1,
                         int const numerador2, int const denominador2
                         Racional const r1, Racional const r2)
{
    assert(r1.denominador1 != 0 and r2.denominador2 != 0);

    Racional r;

    r.numerador = r1.numerador1 * r2.denominador2 +
        r2.numerador2 * r1.denominador1;
    r.denominador = r1.denominador1 * r2.denominador2;

    reduzFracção(rnumerador, denominador);

    assert(r.denominador != 0 and mdc(r.numerador, r.denominador) == 1);

    return r;
}

...

O programa pode ser reescrito como:

#include <iostream>
#include <cassert>

using namespace std;

/** Devolve o máximo divisor comum dos inteiros passados como argumento.
    @pre m <> 0 ou n <> 0.
    @post mdc = mdc(m, n). */
int mdc(int const m, int const n) 
{
    assert(m != 0 or n != 0);
    ...
}

/** Representa números racionais. */
class Racional {
  public:
    int numerador;
    int denominador;
};

/** Reduz a fracção que representa o racional recebidao como argumento.
    @pre r.denominador <> 0 e numerador = n e denominador = d e r = r.
    @post r.denominador <> 0 e mdc(r.numerador, r.denominador) = 1 e
        numerador/denominador = n/d r = r. */
void reduzFracção(int& numerador, int& denominadorRacional& r)
{
    assert(r.denominador != 0);

    int k = mdc(r.numerador, r.denominador);

    r.numerador /= k;
    r.denominador /= k;

    assert(r.denominador != 0 and mdc(r.numerador, r.denominador) == 1);
}

/** Lê do teclado uma fracçãoracional, na forma de dois inteiros sucessivos.
    @pre numerador = n e denominador = dr = r.
    @post Se cin.good() e cin tem dois inteiros n' e d' disponíveis para
        leitura, com d' <> 0, então
        numerador/denominadorr = n'/d' e
        0 < r.denominador e mdc(r.numerador, r.denominador) = 1,
        senão numerador = n e denominador = dr = r e ¬cin.good(). */
void lêParaFracção(int& numerador, int& denominadorRacional& r)
{
    int n, d;

    cin >> n >> d;
    if(cin.good())
        if(d == 0)
            cin.setstate(ios_base::failbit);
        else {
            if(d < 0) {
                r.numerador = -n;
                r.denominador = -d;
            } else {
                r.numerador = n;
                r.denominador = d;
            }
            reduzFracção(numerador, denominadorr);

            assert(0 < r.denominador and mdc(r.numerador, r. denominador) == 1 and
                   r.numerador * d == n * r.denominador and cin.good());

            return;
        }

    assert(not cin.good());
}

/** Devolve a soma de dois racionais.
    @pre r1.denominador <> 0 e r2.denominador <> 0.
    @post somaDe = r1 + r2 e
           somaDe.denominador <> 0 e mdc(somaDe.numerador, somaDe.denominador) = 1. */
Racional somaDe(Racional const r1, Racional const r2)
{
    assert(r1.denominador != 0 and r2.denominador != 0);

    Racional r;

    r.numerador = r1.numerador * r2.denominador +
        r2.numerador * r1.denominador;
    r.denominador = r1.denominador * r2.denominador;

    reduz(r);

    assert(r.denominador != 0 and mdc(r.numerador, r.denominador) == 1);

    return r;
}

/** Escreve uma fracçãoum racional no ecrã no formato usualde uma fracção.
    @pre V.
    @post ¬cout.good() ou cout contém n/d  (ou simplesmente
          n, se d = 1) em que n e d são os valores de r.numerador e r.denominador. */
void escreveFracção(int const numerador, int const denominador
                    Racional const r)
{
    cout << r.numerador;
    if(r.denominador != 1)
        cout << '/' << r.denominador;
}

int main()
{
    // Ler fracções:
    cout << "Introduza duas fracções (numerador denominador): ";
    int n1, d1, n2, d2;
    Racional r1, r2;
    lêParaFracção(r1);
    lêParaFracção(r2);

    if(not cin) {
        cout << "Opps!  A leitura das fracçõesdos racionais falhou!" << endl;
        return 1;
    }

    // Calcular fracçãoracional soma reduzida:
    int n, d;
    somaFracção(n, d, n1, d1, n2, d2);
    Racional r = somaDe(r1, r2);

    // Escrever resultado:
    cout << "A soma de ";
    escreveFracção(n1, d1r1);
    cout << " com ";
    escreveFracção(n1, d1r2);
    cout << " é ";
    escreveFracção(n1, d1r);
    cout << '.' << endl;
}

Repare-se no código:

Racional a;
a.numerador = 10;
a.denominador = 0;

int a = 10; // ou
int a(10);

1. Como conseguir inicializar variáveis de um TAD?
2. Como evitar inicializações inválidas?

Quando se constrói uma variável de um TAD, diz-se que se está a instanciar a classe.  Quando uma variável é construída, é invocado um procedimento especial que se chama construtor do TAD.  Como nós não definimos esse construtor, o C++ forneceu um automaticamente, mas que não faz nada!  Devemos ser nós a defini-lo.  Se quisermos que os racionais sejam sempre inicializados por omissão com zero (fracção 0/1), podemos fazer:

...

/** Representa números racionais. */
class Racional {
  public:
    /** Constrói racional com valor inteiro.
        @pre V.
        @post *this = n e 0 < denominador e 
               mdc(numerador, denominador) = 1. */
    Racional(int const n = 0);

    /** Constrói racional correspondente a n/d.
        @pre d <> 0.
        @post *this = n/d e 0 < denominador e 
               mdc(numerador, denominador) = 1. */
    Racional(int const n, int const d);

    int numerador;
    int denominador;
};

Racional::Racional(int const n)
    : numerador(n), denominador(1)
{
    assert(0 < denominador and mdc(numerador, denominador) == 1);
}

Racional::Racional(int const n, int const d) 
{
    assert(d != 0);

    if(d < 0) {
        numerador = -n;
        denominador = -d;
    } else {
        numerador = n;
        denominador = d;
    }

    reduz(*this);

    assert(0 < denominador and mdc(numerador, denominador) == 1 and 
           numerador * d == n * denominador);
}

...

Explicar significado de *this.  Explicar variável (e não instância) implícita.

Usou-se uma lista de inicializadores no primeiro construtor!  Explicar sintaxe!

Pontos importantes:

1. Pode haver sobrecarga de mais do que um construtor.
2. Os construtores são rotinas membro, tal como numerador é uma variável membro, mas cujo nome é igual ao nome da classe e para os quais não se usa nem pode usar tipo tipo de devolução (pois está implícito no nome da rotina).
3. Às rotinas membro chama-se operações.
4. Dentro de um método os atributos da variável implícita estão directamente acessíveis.
5. As operações são declaradas na classe C++ e definidas fora.  À definição de uma operação chama-se método.  Para que o compilador saiba que são métodos, i.e., implementações de operações do TAD, precede-se o seu nome do nome do TAD e de ::.

Os construtores garantem não só que a fracção que representa o racional está reduzida, mas também que tem denominador positivo!  Porquê?  Explicar que a representação é única!

Agora é possível escrever:

Racional r1;
Racional r2(6, 9);

escreve(r1);
escreve(r2);

0 e 2/3

Como desejado!

Mas o que fizemos não impede acções maldosas ou descuidadas do programador utilizador da classe:

Racional r;
r.denominador = 0;

É de novo o Princípio do encapsulamento: Tudo o que pode ser privado deve ser privado!

Logo, o TAD pode ser melhorado para:

...

/** Representa números racionais. */
class Racional {
  public:
    /** Constrói racional com valor inteiro.
        @pre V.
        @post *this = n e 0 < denominador e 
               mdc(numerador, denominador) = 1. */
    Racional(int const n = 0);

    /** Constrói racional correspondente a n/d.
        @pre d <> 0.
        @post *this = n/d e 0 < denominador e 
               mdc(numerador, denominador) = 1. */
    Racional(int const n, int const d);

  private:
    int numerador;
    int denominador;
};

Racional::Racional(int const n)
    : numerador(n), denominador(1)
{
    assert(0 < denominador and mdc(numerador, denominador) == 1 and
           numerador = denominador * n);
}

Racional::Racional(int const n, int const d) 
{
    assert(d != 0);

    if(d < 0) {
        numerador = -n;
        denominador = -d;
    } else {
        numerador = n;
        denominador = d;
    }

    reduz(*this);

    assert(0 < denominador and mdc(numerador, denominador) == 1 and 
           numerador * d == n * denominador);
}

...

Regra:  Todos os atributos das classes C++ devem ser privados.

Possíveis excepções:  As constantes membro podem ocasionalmente ser públicas, embora não seja geralmente recomendável.

Mas, será que se pode agora escrever

Racional r(6, 9);

escreve(r);

/** Representa números racionais. */
class Racional {
  public:
    /** Constrói racional com valor inteiro.
        @pre V.
        @post *this = n e 0 < denominador e 
               mdc(numerador, denominador) = 1. */
    Racional(int const n = 0);

    /** Constrói racional correspondente a n/d.
        @pre d <> 0.
        @post *this = n/d e 0 < denominador e 
               mdc(numerador, denominador) = 1. */
    Racional(int const n, int const d);

    /** Escreve um racional no ecrã no formato de uma fracção.
        @pre V.
        @post ¬cout.good() ou cout contém n/d  (ou simplesmente
          n, se d = 1) em que n e d são os valores de numerador e denominador. */
    void escreve();

  private:
    int numerador;
    int denominador;
};

...

void Racional::escreve(Racional const r)
{
    cout << r.numerador;
    if(r.denominador != 1)
        cout << '/' << r.denominador;
}

O problema é: como invocar Racional::escreve()?  Simples, se é membro da classe C++, acede-se com o operador ..  Por exemplo:

Racional r1, r2(6, 9);

r1.escreve();
r2.escreve();

A variável é implícita durante a execução dos métodos, mas geralmente é explícita durante a invocação das correspondentes operações.

Nota:  No segundo semestre se verá que as classes propriamente ditas podem ter mais do que um método associado a cada operação.

Resolvemos o problema para o procedimento escreve(), mas é necessário fazer o mesmo para todas as outras rotinas que acedem directamente às variáveis membro!

#include <iostream>
#include <cassert>

using namespace std;

/** Devolve o máximo divisor comum dos inteiros passados como argumento.
    @pre m <> 0 ou n <> 0.
    @post mdc = mdc(m, n). */
int mdc(int const m, int const n) 
{
    assert(m != 0 or n != 0);
    ...
}

/** Representa números racionais. */
class Racional {
  public:
    /** Constrói racional com valor inteiro.
        @pre V.
        @post *this = n e 0 < denominador e 
               mdc(numerador, denominador) = 1. */
    Racional(int const n = 0);

    /** Constrói racional correspondente a n/d.
        @pre d <> 0.
        @post *this = n/d e 0 < denominador e 
               mdc(numerador, denominador) = 1. */
    Racional(int const n, int const d);

    /** Escreve um racional no ecrã no formato de uma fracção.
        @pre V.
        @post ¬cout.good() ou o ecrã contém n/d  (ou simplesmente
              n, se d = 1) em que n e d são os valores de numerador e denominador. */
    void escreve();

    /** Devolve a soma de dois racionais com o racional recebido como argumento.
        @pre r1.denominador <> 0 e r2.denominador <> 0.
        @post somaCom = r1*this + r2 e denominador <> 0
               somaCom.denominador <> 0 e
               mdc(somaCom.numerador, somaCom.denominador) = 1. */
    Racional somaCom(Racional const r2);

    /** Lê do teclado umo racional, na forma de dois inteiros sucessivos.
        @pre r*this = r.
        @post Se cin.good() e cin tem dois inteiros n' e d' disponíveis para
              leitura, com d' <> 0,
              então r*this = n'/d' e 0 < r.denominador e mdc(r.numerador, r.denominador) = 1,
              senão r*this = r e ¬cin.good(). */
    void lê();

  private:
    int numerador;
    int denominador;

    /** Reduz a fracção que representa o racional recebido como argumento.
        @pre r.denominador <> 0 e *this = r.
        @post r.denominador <> 0 e mdc(r.numerador, r.denominador) = 1 e
            *this = r. */
    void reduz();
};

Racional::Racional(int const n)
    : numerador(n), denominador(1)
{
    assert(0 < denominador and mdc(numerador, denominador) == 1 and
           numerador = denominador * n);
}

Racional::Racional(int const n, int const d) 
{
    assert(d != 0);

    if(d < 0) {
        numerador = -n;
        denominador = -d;
    } else {
        numerador = n;
        denominador = d;
    }

    reduz();

    assert(0 < denominador and mdc(numerador, denominador) == 1 and 
           numerador * d == n * denominador);
}

void Racional::escreve()
{
    cout << numerador;
    if(denominador != 1)
        cout << '/' << denominador;
}

Racional Racional::somaCom(Racional const r1, Racional const r2)
{
    assert(r1.denominador != 0 and r2.denominador != 0);

    Racional r;

    r.numerador = r1.numerador * r2.denominador +
        r2.numerador * r1.denominador;
    r.denominador = r1.denominador * r2.denominador;

    r.reduz(r);

    assert(denominador != 0 and
           r.denominador != 0 and mdc(r.numerador, r.denominador) == 1);

    return r;
}

void Racional::lê(Racional& r)
{
    int n, d;

    cin >> n >> d;
    if(cin.good())
        if(d == 0)
            cin.setstate(ios_base::failbit);
        else {
            if(d < 0) {
                r.numerador = -n;
                r.denominador = -d;
            } else {
                r.numerador = n;
                r.denominador = d;
            }
            reduz(r);

            assert(0 < r.denominador and mdc(r.numerador, r.denominador) == 1 and
                   r.numerador * d == n * r.denominador and cin.good());

            return;
        }

    assert(not cin.good());
}

void Racional::reduz(Racional& r)
{
    assert(r.denominador != 0);

    int k = mdc(r.numerador, r.denominador);

    r.numerador /= k;
    r.denominador /= k;

    assert(r.denominador != 0 and mdc(r.numerador, r.denominador) == 1);
}

int main()
{
    // Ler fracções:
    cout << "Introduza duas fracções (numerador denominador): ";
    Racional r1, r2;
    r1.lê(r1);
    r2.lê(r2);

    if(not cin) {
        cout << "Opps!  A leitura dos racionais falhou!" << endl;
        return 1;
    }

    // Calcular racional soma:
    Racional r = r1.somaCom(r1, r2);

    // Escrever resultado:
    cout << "A soma de ";
    r1.escreve(r1);
    cout << " com ";
    r2.escreve(r2);
    cout << " é ";
    r.escreve(r);
    cout << '.' << endl;
}

Explicar reduz() privada!  Explicar explicitação da instância implícita (*this).reduz()!

Deixar claro que não há qualquer razão para mdc() ser membro do TAD!  É de utilidade geral (não neste programa, mas na generalidade dos programas...)

Ok.  r1.lê() é aceitável, mas r = r1.somaCom(r2) é horrendo!  A ver na próxima aula...

Atenção!  Referir problema com

Racional r(6/9);

Uma classe C++ é também um módulo!  Aliás, as classes são os módulos por excelência em C++!

Interface

Parte pública, incluindo operações

Implementação

Parte privada e implementação das operações: os métodos

Manual de utilização (contrato)

Comentário de documentação da classe
Manual de utilização de cada operação pública

Como desenhar um TAD?  Começar, como sempre, pela interface e pelo manual de utilização.

Vamos agora fazer um pequeno exercício.  Gostava que identificassem uma única condição especial.  Tem de envolver apenas os atributos do TAD.  Deve ser pelo menos tão forte quanto a pré-condição de cada método.  E deve ser garantidamente verificada no final dos métodos públicos, admitindo que o é no seu início (excepto para o construtor).

Partindo das pré-condições:

• Racional(int): Não tem pré-condições envolvendo atributos, pois não existem!
• Racional(int, int): Idem!
• escreve(): V.
• somaCom(): denominador <> 0.
• lê(): V.

Daqui se tira que a condição mais forte é: denominador <> 0.

Partindo das condições objectivo:

• Racional(int): 0 < denominador e mdc(numerador, denominador) = 1.
• Racional(int, int): 0 < denominador e mdc(numerador, denominador) = 1.
• escreve(): tudo o que se verificar no início, também se verifica no fim, pois não altera nada.
• somaCom(): 0 <> denominador e mdc(numerador, denominador) = 1.  Mas se ambos os denominadores forem positivos no início, então 0 < denominador. 
• lê(): 0 < denominador e mdc(numerador, denominador) = 1 (se houver erro, o que se verificar à partida também se verifica no fim).

Qual será então a condição objectivo mais forte que se verifica sempre?

É 

0 < denominador e mdc(numerador, denominador) = 1

desde que esta condição se verifique também sempre no início (excepto nos construtores)!

Esta condição é muito importante.  Chama-se-lhe a Condição Invariante da Classe (CIC), e diz o que se deve verificar sempre para que a representação de um racional esteja correcta!

Então é possível explicitar essa condição no código, incluindo verificações do seu cumprimento através de instruções de asserção.  O seu objectivo é, mais uma vez, verificar erros do programador!

Como a condição se deve verificar no início e no final de cada método público, elimina-se da documentação dos métodos e acrescenta-se na documentação da classe (embora diga respeito apenas à implementação dos racionais).

Inclui-se uma instrução de asserção para verificar o cumprimento da condição invariante da classe no início e no final de cada método público:

#include <iostream>
#include <cassert>

using namespace std;

/** Devolve o máximo divisor comum dos inteiros passados como argumento.
    @pre m <> 0 ou n <> 0.
    @post mdc = mdc(m, n). */
int mdc(int const m, int const n) 
{
    assert(m != 0 or n != 0);
    ...
}

/** Representa números racionais.  
    @invariant 0 < denominador e mdc(numerador, denominador) = 1. */
class Racional {
  public:
    /** Constrói racional com valor inteiro.
        @pre V.
        @post *this = n e 0 < denominador e 
               mdc(numerador, denominador) = 1. */
    Racional(int const n = 0);

    /** Constrói racional correspondente a n/d.
        @pre d <> 0.
        @post *this = n/d e 0 < denominador e 
               mdc(numerador, denominador) = 1. */
    Racional(int const n, int const d);

    /** Escreve um racional no ecrã no formato de uma fracção.
        @pre V.
        @post ¬cout.good() ou o ecrã contém n/d  (ou simplesmente
              n, se d = 1) em que n e d são os valores de numerador e denominador. */
    void escreve();

    /** Devolve a soma com o racional recebido como argumento.
        @pre V.
        @post somaCom = *this + r2 e denominador <> 0 e
               somaCom.denominador <> 0 e
               mdc(somaCom.numerador, somaCom.denominador) = 1. */
    Racional somaCom(Racional const r2);

    /** Lê do teclado o racional, na forma de dois inteiros sucessivos.
        @pre *this = r.
        @post Se cin.good() e cin tem dois inteiros n' e d' disponíveis para
            leitura, com d' <> 0,
            então *this = n'/d' e
            0 < denominador e mdc(numerador, denominador) = 1,
            senão *this = r e ¬cin.good(). */
    void lê();

  private:
    int numerador;
    int denominador;

    /** Reduz a fracção que representa o racional.
        @pre denominador <> 0 e *this = r.
        @post denominador <> 0 e mdc(numerador, denominador) = 1 e
            *this = r. */
    void reduz();

    /** Indica se a CIC se verifica.
        @pre V.
        @post  cumpreInvariante = 0 < denominador e mdc(numerador, denominador) = 1. */
    bool cumpreInvariante();
};

Racional::Racional(int const n)
    : numerador(n), denominador(1)
{
    assert(0 < denominador and mdc(numerador, denominador) == 1 and
           numerador = denominador * n);

    assert(cumpreInvariante());

    assert(numerador == n * denominador);
}

Racional::Racional(int const n, int const d) 
{
    assert(d != 0);

    if(d < 0) {
        numerador = -n;
        denominador = -d;
    } else {
        numerador = n;
        denominador = d;
    }

    reduz();

    assert(0 < denominador and mdc(numerador, denominador) == 1 and
           numerador * d == n * denominador);
    assert(cumpreInvariante());

    assert(numerador * d == n * denominador);
}

void Racional::escreve()
{
    assert(cumpreInvariante());

    cout << numerador;
    if(denominador != 1)
        cout << '/' << denominador;

    assert(cumpreInvariante());
}

Racional Racional::somaCom(Racional const r2)
{
    assert(denominador != 0 and r2.denominador != 0);
    assert(cumpreInvariante() and r2.cumpreInvariante());

    Racional r;

    r.numerador = numerador * r2.denominador +
        r2.numerador * denominador;
    r.denominador = denominador * r2.denominador;

    r.reduz();

    assert(denominador != 0 and
           r.denominador != 0 and mdc(r.numerador, r.denominador) == 1);
    assert(cumpreInvariante() and r.cumpreInvariante());

    return r;
}

void Racional::lê()
{
    assert(cumpreInvariante());

    int n, d;

    cin >> n >> d;
    if(cin.good())
        if(d == 0)
            cin.setstate(ios_base::failbit);
        else {
            if(d < 0) {
                numerador = -n;
                denominador = -d;
            } else {
                numerador = n;
                denominador = d;
            }
            reduz();

            assert(cumpreInvariante());

            assert(0 < denominador and mdc(numerador, denominador) == 1 and
                   numerador * d == n * denominador and cin.good());

            return;
        }

    assert(cumpreInvariante());

    assert(not cin.good());
}

void Racional::reduz()
{
    assert(denominador != 0);

    int k = mdc(numerador, denominador);

    numerador /= k;
    denominador /= k;

    assert(denominador != 0 and mdc(numerador, denominador) == 1);
}

bool Racional::cumpreInvariante()
{
    return 0 < denominador and mdc(numerador, denominador) == 1;
}

int main()
{
    // Ler fracções:
    cout << "Introduza duas fracções (numerador denominador): ";
    Racional r1, r2;
    r1.lê();
    r2.lê();

    if(not cin) {
        cout << "Opps!  A leitura dos racionais falhou!" << endl;
        return 1;
    }

    // Calcular racional soma:
    Racional r = r1.somaCom(r2);

    // Escrever resultado:
    cout << "A soma de ";
    r1.escreve();
    cout << " com ";
    r2.escreve();
    cout << " é ";
    r.escreve();
    cout << '.' << endl;
}

Versão final desta aula:

#include <iostream>
#include <cassert>

using namespace std;

/** Devolve o máximo divisor comum dos inteiros passados como argumento.
    @pre m <> 0 ou n <> 0.
    @post mdc = mdc(m, n). */
int mdc(int const m, int const n) 
{
    assert(m != 0 or n != 0);
    ...
}

/** Representa números racionais.  
    @invariant 0 < denominador e mdc(numerador, denominador) = 1. */
class Racional {
  public:
    /** Constrói racional com valor inteiro.
        @pre V.
        @post *this = n. */
    Racional(int const n = 0);

    /** Constrói racional correspondente a n/d.
        @pre d <> 0.
        @post *this = n/d. */
    Racional(int const n, int const d);

    /** Escreve um racional no ecrã no formato de uma fracção.
        @pre V.
        @post ¬cout.good() ou o ecrã contém n/d  (ou simplesmente
              n, se d = 1) em que n e d são os valores de numerador e denominador. */
    void escreve();

    /** Devolve a soma com o racional recebido como argumento.
        @pre V.
        @post somaCom = *this + r2. */
    Racional somaCom(Racional const r2);

    /** Lê do teclado o racional, na forma de dois inteiros sucessivos.
        @pre *this = r.
        @post Se cin.good() e cin tem dois inteiros n' e d' disponíveis para
              leitura, com d' <> 0,
              então *this = n'/d',
              senão *this = r e ¬cin. */
    void lê();

  private:
    int numerador;
    int denominador;

    /** Reduz a fracção que representa o racional.
        @pre denominador <> 0 e *this = r.
        @post denominador <> 0 e mdc(numerador, denominador) = 1 e
            *this = r. */
    void reduz();

    /** Indica se a CIC se verifica.
        @pre V.
        @post  cumpreInvariante = 0 < denominador e mdc(numerador, denominador) = 1. */
    bool cumpreInvariante();
};

Racional::Racional(int const n)
    : numerador(n), denominador(1)
{
    assert(cumpreInvariante());

    assert(numerador == n * denominador);
}

Racional::Racional(int const n, int const d) 
{
    assert(d != 0);

    if(d < 0) {
        numerador = -n;
        denominador = -d;
    } else {
        numerador = n;
        denominador = d;
    }

    reduz();

    assert(cumpreInvariante());

    assert(numerador * d == n * denominador);
}

void Racional::escreve()
{
    assert(cumpreInvariante());

    cout << numerador;
    if(denominador != 1)
        cout << '/' << denominador;

    assert(cumpreInvariante());
}

Racional Racional::somaCom(Racional const r2)
{
    assert(cumpreInvariante() and r2.cumpreInvariante());

    Racional r;

    r.numerador = numerador * r2.denominador +
        r2.numerador * denominador;
    r.denominador = denominador * r2.denominador;

    r.reduz();

    assert(cumpreInvariante() and r.cumpreInvariante());

    return r;
}

void Racional::lê()
{
    assert(cumpreInvariante());

    int n, d;

    cin >> n >> d;
    if(cin.good())
        if(d == 0)
            cin.setstate(ios_base::failbit);
        else {
            if(d < 0) {
                numerador = -n;
                denominador = -d;
            } else {
                numerador = n;
                denominador = d;
            }
            reduz();

            assert(cumpreInvariante());

            assert(numerador * d == n * denominador and cin.good());

            return;
        }

    assert(cumpreInvariante());

    assert(not cin.good());
}

void Racional::reduz()
{
    assert(denominador != 0);

    int k = mdc(numerador, denominador);

    numerador /= k;
    denominador /= k;

    assert(denominador != 0 and mdc(numerador, denominador) == 1);
}

bool Racional::cumpreInvariante()
{
    return 0 < denominador and mdc(numerador, denominador) == 1;
}

int main()
{
    // Ler fracções:
    cout << "Introduza duas fracções (numerador denominador): ";
    Racional r1, r2;
    r1.lê();
    r2.lê();

    if(not cin) {
        cout << "Opps!  A leitura dos racionais falhou!" << endl;
        return 1;
    }

    // Calcular racional soma:
    Racional r = r1.somaCom(r2);

    // Escrever resultado:
    cout << "A soma de ";
    r1.escreve();
    cout << " com ";
    r2.escreve();
    cout << " é ";
    r.escreve();
    cout << '.' << endl;
}