Guião da 11ª Aula Teórica

Sumário

  1. Revisões sobre a aula anterior.
  2. De novo a noção de condição invariante de classe (CIC): regras e vantagens.
  3. Importância das restrições às variáveis membro: a cada racional deve corresponder uma representação única.
  4. Introdução à sobrecarga de operadores para classes C++: operadores + binário e ++ prefixo.
  5. Devolução de referências.
  6. Acesso à instância implícita através da construção *this.

Rever todo o programa da aula passada.  Aproveitar para explicar que com class os membros são privados salvo indicação em contrário, e com struct são públicos salvo indicação em contrário.

Atenção!  Esta revisão é profunda (deve incluir um traçado do programa)!  Daí a dimensão reduzida do guião.  Mencionar cuidadosamente a CIC e acrescentar noções sobre passagem de argumentos por referência constante!

#include <iostream>
#include <cassert>

using namespace std;

/** Devolve o máximo divisor comum dos inteiros passados como argumento.
    @pre m <> 0 ou n <> 0.
    @post mdc = mdc(m, n). */
int mdc(int const m, int const n) 
{
    assert(m != 0 or n != 0);
    ...
}

/** Representa números racionais.  
    @invariant 0 < denominador e mdc(numerador, denominador) = 1. */
class Racional {
  public:
    /** Constrói racional com valor inteiro.
        @pre V.
        @post *this = valor. */
    Racional(int const valor = 0);

    /** Constrói racional correspondente a n/d.
        @pre d <> 0.
        @post *this = numerador/denominador. */
    Racional(int const numerador, int const denominador);

    /** Escreve um racional no ecrã no formato de uma fracção.
        @pre V.
        @post ¬cout.good() ou cout contém n/d (ou simplesmente
              n, se d = 1) em que n e d são os valores de numerador e denominador. */
    void escreve();

    /** Devolve a soma com o racional recebido como argumento.
        @pre V.
        @post somaCom = *this + r2. */
    Racional somaCom(Racional const& r2);

    /** Lê do teclado o racional, na forma de dois inteiros sucessivos.
        @pre *this = r.
        @post Se cin.good() e cin tem dois inteiros n' e d' disponíveis para
            leitura, com d' <> 0,
            então *this = n'/d',
            senão *this = r e ¬cin.good(). */
    void lê();

  private:
    int numerador;
    int denominador;

    /** Reduz a fracção que representa o racional.
        @pre denominador <> 0 e *this = r.
        @post denominador <> 0 e mdc(numerador, denominador) = 1 e
            *this = r. */
    void reduz();

    /** Indica se a CIC se verifica.
        @pre V.
        @post cumpreInvariante = 0 < denominador e mdc(numerador, denominador) = 1. */
    bool cumpreInvariante();
};

Racional::Racional(int const valor)
    : numerador(valor), denominador(1)
{

    assert(cumpreInvariante());
    assert(numerador == valor * denominador);
}

Racional::Racional(int const numerador_, int const denominador_) 
{
    assert(denominador_ != 0);

    if(denominador_ < 0) {
        numerador = -numerador_;
        denominador = -denominador_;
    } else {
        numerador = numerador_;
        denominador = denominador_;
    }

    reduz();

    assert(cumpreInvariante());

    assert(numerador * denomindor_ == numerador_ * denominador);
}

void Racional::escreve()
{
    assert(cumpreInvariante());

    cout << numerador;
    if(denominador != 1)
        cout << '/' << denominador;

    assert(cumpreInvariante());

}

Racional Racional::somaCom(Racional const& r2)
{
    assert(cumpreInvariante() and r2.cumpreInvariante());

    Racional r;

    r.numerador = numerador * r2.denominador +
        r2.numerador * denominador;
    r.denominador = denominador * r2.denominador;

    r.reduz();

    assert(cumpreInvariante() and r.cumpreInvariante());

    return r;
}

void Racional::lê()
{
    assert(cumpreInvariante());

    int n, d;

    cin >> n >> d;
    if(cin.good())
        if(d == 0)
            cin.setstate(ios_base::failbit);
        else {
            if(d < 0) {
                numerador = -n;
                denominador = -d;
            } else {
                numerador = n;
                denominador = d;
            }
            reduz();

            assert(cumpreInvariante());

            assert(numerador * d == n * denominador and cin.good());

            return;
        }

    assert(cumpreInvariante());

    assert(not cin.good());
}

void Racional::reduz()
{
    assert(denominador != 0);

    int k = mdc(numerador, denominador);

    numerador /= k;
    denominador /= k;

    assert(denominador != 0 and mdc(numerador, denominador) == 1);
}

bool Racional::cumpreInvariante()
{
    return 0 < denominador and mdc(numerador, denominador) == 1;
}

int main()
{
    // Ler fracções:
    cout << "Introduza duas fracções (numerador denominador): ";
    Racional r1, r2;
    r1.lê();
    r2.lê();

    if(not cin) {
        cout << "Opps!  A leitura dos racionais falhou!" << endl;
        return 1;
    }

    // Calcular racional soma:
    Racional r = r1.somaCom(r2);

    // Escrever resultado:
    cout << "A soma de ";
    r1.escreve();
    cout << " com ";
    r2.escreve();
    cout << " é ";
    r.escreve();
    cout << '.' << endl;
}

Na aula passada disse-vos que a notação a que a utilização de operações do TAD definido obrigava era algo estranha, pelo menos para o principiante, especialmente quando usada para somar dois racionais.  Hoje, entre outros assuntos, vamos ver como se pode melhorar essa notação.

Mostrar, discutir e explicar objectivo.

O C++ proporciona-nos a possibilidade de sobrecarregar os operadores (+, -, *, /, ==, etc.) de modo a poderem ser utilizados com novos tipos definidos por nós.  Essa sobrecarga pode ser feita por rotinas normais ou por rotinas membro de uma classe C++, ou operações.

Para que a função membro somaCom() possa ser invocada através do operador + é necessário modificar o seu nome:

...

class Racional {
  public:
    ...
    Racional operator+(Racional const& r2);
    ...
};

...

Racional Racional::operator+(Racional const& r2)
{
    assert(cumpreInvariante() and r2.cumpreInvariante());

    Racional r;

    r.numerador = numerador * r2.denominador +
        r2.numerador * denominador;
    r.denominador = denominador * r2.denominador;

    r.reduz();

    assert(cumpreInvariante() and r.cumpreInvariante());

    return r;
}

...

int main()
{
    ...

    // Calcular racional soma:
    Racional r = r1.soma(r2) + r2;

    // Escrever resultado:
    cout << "A soma de ";
    r1.escreve();
    cout << " com ";
    r2.escreve();
    cout << " é ";
    r.escreve();
    cout << '.' << endl;
}

Falta agora fazer o mesmo para todos os operadores de interesse para os racionais.  Quais são eles?  São:

++, -- sufixo
++, -- prefixo
+, - unários
*, /
+, - binários
<, <=, >, >=
== !=
*=
/=
+=
-=

Uma questão importante é o que é que devolvem os operadores op= e os operadores ++ e -- prefixo.  Suponha-se o código:

int i = 0;
++(++i);
cout << i << endl;

Que resulta?  2? Claro!  Mas então, o operador ++ para além de incrementar i devolve o próprio i e não uma sua cópia!  

Atenção!  Como sempre deve-se usar a notação UML estendida para mostrar o efeito dos troços de código.  Atenção à notação estendida para as referências!

Escreva-se um procedimento incrementa com o mesmo efeito.  Como deve aumentar i, deve receber o argumento por referência:

void incrementa(int& v)
{
    v = v + 1;
}

...

int i = 0;
++(++i)incrementa(incrementa(i));
cout << i << endl;

Impossível!  incrementa() não devolve nada!  Tentemos:

voidint incrementa(int& v)
{
    v = v + 1;

    return v;
}

...

int i = 0;
incrementa(incrementa(i));
cout << i << endl;

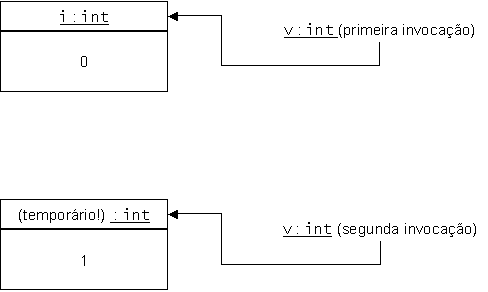
Não funciona!  Valor incrementado é uma cópia temporária de i.  Se compilasse (e não compila), só incrementava i uma vez.

É necessário devolver o próprio i!

int& incrementa(int& v)
{
    v = v + 1;

    return v; // ou simplesmente return v = v + 1;
}

...

int i = 0;
incrementa(incrementa(i));
cout << i << endl;

ou seja

Agora sim!

Vamos implementar o operador ++ prefixo para os racionais.  

Como precisa de alterar as variáveis membro privadas, deve ser um operador membro:

...

class Racional {
  public:
    ...
    /** Incrementa o racional.
        @pre *this = r.
        @post *this = r + 1. */
    Racional& operator++();
    ...
};

...

Racional& Racional::operator++()
{
    assert(cumpreInvariante());

    Discutir este código!  Porque não é necessário reduzir?

    numerador += denominador;

    assert(cumpreInvariante());

    return ?Que devolver?
}

...

Que devolver?  Devia ser a própria variável implícita, à qual pertencem os atributos numerador e denominador!  É possível referirmo-nos à variável implícita explicitamente através de *this (significa eu).  Logo:

...

class Racional {
  public:
    ...
    /** Incrementa o racional.
        @pre *this = r.
        @post operator++ idêntico a *this e *this = r + 1. */
    Racional& operator++();
    ...
};

...

Racional& Racional::operator++()
{
    assert(cumpreInvariante());

    numerador += denominador;

    assert(cumpreInvariante());

    return *this;
}

...

Chamaremos a isto a explicitação da variável implícita.

Explicar o que significa idêntico!  Diferença entre igualdade e identidade.

Se houver tempo, falar da diferença entre 

int cópia(int const& v)
{
    return v;
}

e

int& mesmo(int& v)
{
    return v;
}

Discutir utilizações.  Mencionar conceito de lvalue (left value).

Falar um pouco de testes de unidade e da sua enorme importância.

Se houver tempo continuar com +=, passando + a não membro.