Guião da 13ª Aula Teórica

Sumário

  1. Definindo constantes de uma classe: necessidade de declarar métodos como constantes (que não alteram a instância implícita).  Sintaxe.  Devolução por valor constante.
  2. Evitando o mecanismo de invocação de rotinas no código máquina produzido pelo compilador: rotinas inline.  Sintaxe.  Regras de utilização.
  3. Explicação do efeito de inline sobre o código máquina produzido.  Exemplo com programa em C++ e respectiva tradução para MAC-1 (ver Arquitectura de Computadores).

Escrever logo no quadro o programa da soma e as suas versões MAC-1!

Na última aula introduzimos mais alguns operadores nossa classe C++ Racional.  O resultado é o que podem ver no quadro.

#include <iostream>
#include <cassert>

using namespace std;

/** Devolve o máximo divisor comum dos inteiros passados como argumento.
    @pre m <> 0 ou n <> 0.
    @post mdc = mdc(m, n). */
int mdc(int const m, int const n) 
{
    assert(m != 0 or n != 0);

    ...
}

/** Representa números racionais.  
    @invariant 0 < denominador_ e mdc(numerador_, denominador_) = 1. */
class Racional {
  public:
    /** Constrói racional com valor inteiro.
        @pre V.
        @post *this = valor. */
    Racional(int const valor = 0);

    /** Constrói racional correspondente a n/d.
        @pre d <> 0.
        @post *this = numerador/denominador. */
    Racional(int const numerador, int const denominador);

    /** Devolve numerador da fracção mínima correspondente ao racional.
        @pre V.
        @post numerador /denominador() = *this. */
    int numerador();

    /** Devolve denominador da fracção mínima correspondente ao racional.
        @pre V.
        @post (E n : : n/denominador = *this e 0 < denominador e
              mdc(n, denominador) = 1). */
    int denominador();

    /** Escreve um racional no ecrã no formato de uma fracção.
        @pre V.
        @post ¬cout.good() ou cout contém n/d  (ou simplesmente
              n, se d = 1) em que n e d são os valores de numerador() e denominador(). */
    void escreve();

    /** Lê do teclado o racional, na forma de dois inteiros sucessivos.
        @pre *this = r.
        @post Se cin.good() e cin tem dois inteiros n' e d' disponíveis para
              leitura, com d' <> 0,
              então *this = n'/d',
              senão *this = r e ¬cin.good(). */
    void lê();

    /** Incrementa o racional.
        @pre *this = r.
        @post operator++ idêntico a *this e *this = r + 1. */
    Racional& operator++();

    /** Decrementa o racional.
        @pre *this = r.
        @post operator-- idêntico a *this e *this = r - 1. */
    Racional& operator--();

    /** Multiplica por um racional.
        @pre *this = r.
        @post operator*= idêntico a *this e *this = r × r2. */
    Racional& operator*=(Racional const& r2);

    /** Divide por um racional.
        @pre *this = r e r2 <> 0.
        @post operator/= idêntico a *this e *this = r / r2. */
    Racional& operator/=(Racional const& r2);

    /** Adiciona de um racional.
        @pre *this = r.
        @post operator+= idêntico a *this e *this = r + r2. */
    Racional& operator +=(Racional const& r2);

    /** Subtrai de um racional.
        @pre *this = r.
        @post operator-= idêntico a *this e *this = r - r2. */
    Racional& operator-=(Racional const& r2);

  private:
    int numerador_;
    int denominador_;

    /** Reduz a fracção que representa o racional.
        @pre denominador_ <> 0 e *this = r.
        @post denominador_ <> 0 e mdc(numerador_, denominador_) = 1 e
            *this = r. */
    void reduz();

    /** Indica se a CIC se verifica.
        @pre V.
        @post cumpreInvariante = 0 < denominador_ e mdc(numerador_, denominador_) = 1. */
    bool cumpreInvariante();
};

Racional::Racional(int const valor)
    : numerador_(valor), denominador_(1)
{

    assert(cumpreInvariante());
    assert(numerador() == valor * denominador());
}

Racional::Racional(int const numerador, int const denominador) 
{
    assert(denominador != 0);

    if(denominador < 0) {
        numerador_ = -numerador;
        denominador_ = -denominador;
    } else {
        numerador_ = numerador;
        denominador_ = denominador;
    }

    reduz();

    assert(cumpreInvariante());
    assert(numerador_() * denominador == numerador * denominador());
}

int Racional::numerador()
{
    assert(cumpreInvariante());

    assert(cumpreInvariante());

    return numerador_;
}

int Racional::denominador()
{
    ...
}

void Racional::escreve()
{
    ...
}

void Racional::lê()
{
    ...
}

Racional& Racional::operator++()
{
    ...
}

Racional& Racional::operator--()
{
    ...
}

Racional& Racional::operator*=(Racional const& r2)
{
    ...
}

Racional& Racional::operator/=(Racional const& r2)
{
    ...
}

Racional& Racional::operator+=(Racional const& r2)
{
    assert(cumpreInvariante() and r2.cumpreInvariante());

    numerador_ = numerador_ * r2.denominador_ +
        r2.numerador_ * denominador_;
    denominador_ *= r2.denominador_;

    reduz();

    assert(cumpreInvariante());

    return *this;
}

Racional& Racional::operator-=(Racional const& r2)
{
    ...
}

void Racional::reduz()
{
    assert(denominador_ != 0);

    int divisor = mdc(numerador_, denominador_);

    numerador_ /= divisor;
    denominador_ /= divisor;

    assert(denominador_ != 0 and mdc(numerador_, denominador_) == 1);
}

bool Racional::cumpreInvariante()
{
    ...
}

/** Produto de dois racionais.
    @pre V.
    @post operator* = r1 × r2. */
Racional const operator*(Racional r1, Racional const& r2)
{
    ...
}

/** Divisão de dois racionais.
    @pre r2 <> 0.
    @post operator/ = r1 / r2. */
Racional const operator/(Racional r1, Racional const& r2)
{
    ...
}

/** Soma de dois racionais.
    @pre V.
    @post operator+ = r1 + r2. */
Racional const operator+(Racional r1, Racional const& r2)
{
    return r1 += r2;
}

/** Subtracção de dois racionais.
    @pre V.
    @post operator- = r1 - r2. */
Racional const operator-(Racional r1, Racional const& r2)
{
    ...
}

/** Devolve verdadeiro se dois racionais forem iguais.
    @pre V.
    @post operator== = (r1 = r2). */
bool operator==(Racional const& r1, Racional const& r2)
{
    return r1.numerador() == r2.numerador() and
           r1.denominador() == r2.denominador();
}

/** Devolve verdadeiro se dois racionais forem iguais.
    @pre V.
    @post operator != = (r1 <> r2). */
bool operator!=(Racional const& r1, Racional const& r2)
{
    ...
}

int main()
{
    ...
}

Ficaram por definir alguns operadores, mas antes de os pensar em definir há que pensar noutros assuntos...

Será que se podem definir constantes racionais?  Sim!

Racional const um_terço(1, 3);

Mas o que acontece quando se faz:

cout << "O denominador é " << um_terço.denominador() << endl;

Dá erro!  O compilador assume que as operações alteram a instância implícita!  E a instância implícita é... constante!

Note-se que o mesmo problema já existia neste código.  Repare-se no operador ==, por exemplo.  Explicar.

Logo, é necessário indicar explicitamente ao compilador quais as operações cujos métodos não alteram a instância implícita, ou seja, que esta funciona como uma constante implícita.

Explicar sintaxe e espalhar const pelo código.  Discutir cuidadosamente a constância da variável implícita: variáveis membro inalteráveis e operações não constantes proibidas!

...

/** Representa números racionais.  
    @invariant 0 < denominador_ e mdc(numerador_, denominador_) = 1. */
class Racional {
  public:

    ...

    /** Devolve numerador da fracção mínima correspondente ao racional.
        @pre V.
        @post numerador /denominador() = *this. */
    int numerador() const;

    /** Devolve denominador da fracção mínima correspondente ao racional.
        @pre V.
        @post (E n : : n/denominador = *this e 0 < denominador e
              mdc(n, denominador) = 1). */
    int denominador() const;

    /** Escreve um racional no ecrã no formato de uma fracção.
        @pre V.
        @post ¬cout.good() ou cout contém n/d  (ou simplesmente
              n, se d = 1) em que n e d são os valores de numerador() e denominador(). */
    void escreve() const;

    ...

  private:

    ...

    /** Indica se a CIC se verifica.
        @pre V.
        @post cumpreInvariante = 0 < denominador_ e mdc(numerador_, denominador_) = 1. */
    bool cumpreInvariante() const;
};

...

int Racional::numerador() const
{
    assert(cumpreInvariante());

    assert(cumpreInvariante());

    return numerador_;
}

int Racional::denominador() const
{
    ...
}

void Racional::escreve() const
{
    ...
}

...

bool Racional::cumpreInvariante() const
{
    ...
}

...

Note-se que nas operações que garantem a constância da instância implícita não é necessário verificar a veracidade da condição invariante no seu final!

As operações podem assim ser divididas em operações que modificam e operações que não modificam a instância implícita.  As segundas dizem-se modificadoras, enquanto as primeiras, pelo menos no caso das funções, dizem-se inspectoras.  Também é típico chamar às funções membro inspectoras interrogações (queries).

Atenção!  É muito importante pensar logo nas operações de uma classe como sendo ou não constantes, ou melhor, como garantindo ou não a constância da instância implícita.

As invocações de rotinas (membro ou não) implicam tarefas de arrumação da casa algo morosas: é necessário colocar na pilha o endereço de retorno e os respectivo argumentos, executar as instruções do corpo da rotina, depois retirar os argumentos da pilha, e retornar, eventualmente devolvendo o resultado no seu topo.  Referir Arquitectura de Computadores e aulas sobre rotinas recursivas (aquela com os pesos).  Suponha-se a invocação:

Racional r(1, 3);

Racional s = r + 2;

Quantas invocações de rotinas são feitas neste código?

Dar dica acerca de construtores por cópia!

  1. Construtor.
  2. reduz().
  3. mdc().
  4. Construtor para converter 2 num racional.
  5. Construtor por cópia (explicar) para copiar o argumento r para o parâmetro r1 do operador +.
  6. Operador +.
  7. Operador +=.
  8. reduz().
  9. mdc().
  10. Construtor por cópia para devolver cópia de r1 no operador +.
  11. Construtor por cópia para inicializar s à custa do valor devolvido pelo operador +.

Não será lento?  Como evitá-lo?  Duma forma simples: rotinas muito simples, tipicamente não fazendo uso de ciclos e consistindo em apenas duas ou três linhas (excluindo instruções de asserção), podem ser em-linha ou inline.  Que significa?  Que o compilador, em vez de traduzir o código da rotina uma vez e chamá-lo quando necessário, coloca o código da rotina directamente nos locais de chamada!  Por exemplo:

inline int soma(int const a, int const b)
{
    return a + b;
}

int main()
{
    int x1 = 10;
    int x2 = 20;
    int x3 = 30;
    int r = 0;

    r = soma(x1, x2);
    r = soma(r, x3);
}

fica com o mesmo código máquina que

int main()
{
    int x1 = 10;
    int x2 = 20;
    int x3 = 30;
    int r = 0;

    r = x1 + x2;
    r = r + x3;
}

É interessante ver-se a tradução para assembly do MAC-1 (citar Arquitectura de Computadores) dos dois programas.

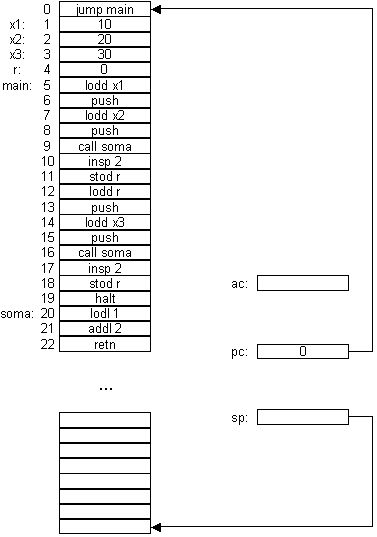
Sem inline:

        jump main

        # Variáveis:

        x1 = 10
        x2 = 20
        x3 = 30
        r  =  0

        # Aqui faz-se a soma:

main:   lodd x1    # Carrega variável x1 no acumulador.
        push       # Coloca acumulador no topo da pilha.
        lodd x2    # Carrega variável x2 no acumulador.
        push       # Coloca acumulador no topo da pilha.
        # Aqui a pilha tem os dois argumentos x1 e x2:
        call soma  # Invoca a função soma.
        insp 2     # Repõe a pilha (limpeza da casa).
        # Aqui o acumulador tem o valor devolvido.
        stod r     # Guarda o acumulador na variável r.

        lodd r     # Carrega variável r no acumulador.
        push       # Coloca acumulador no topo da pilha.
        lodd x3    # Carrega variável x3 no acumulador.
        push       # Coloca acumulador no topo da pilha.
        # Aqui a pilha tem os dois argumentos r e x3:
        call soma  # Invoca a função soma.
        insp 2     # Repõe a pilha (limpeza da casa).
        # Aqui o acumulador tem o valor devolvido.
        stod r     # Guarda o acumulador na variável r.

        halt

soma:   lodl 1
        addl 2
        retn 

Com inline:

        jump main

        # Variáveis:

        x1 = 10
        x2 = 20
        x3 = 30
        r  =  0

        # Aqui faz-se a soma:

main:   lodd x1    # Carrega variável x1 no acumulador.
        addd x2    # Adiciona variável x2 ao acumulador.
        stod r     # Guarda o acumulador na variável r.

        lodd r     # Carrega variável r no acumulador.
        addd x3    # Adiciona variável x3 ao acumulador.
        stod r     # Guarda o acumulador na variável r.

        halt

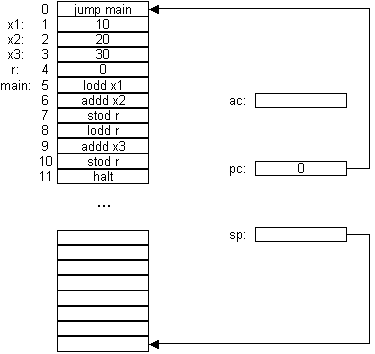
Explicar que programa consome memória!

Explicar que a dimensão do código pode aumentar!  Se as rotinas forem simples, a dimensão do código pode diminuir, que é o que acontece neste caso!

Espalhar inline pelos métodos (tudo excepto lê() e mdc()).  Explicar que basta indicar que são em linha (inline) na definição!

...

inline Racional::Racional(int const valor)
    : numerador_(valor), denominador_(1)
{

    assert(cumpreInvariante());
    assert(numerador() == valor * denominador());
}

inline Racional::Racional(int const numerador, int const denominador) 
{
    ...
}

inline int Racional::numerador()
{
    assert(cumpreInvariante());

    assert(cumpreInvariante());

    return numerador_;
}

inline int Racional::denominador()
{
    ...
}

inline void Racional::escreve()
{
    ...
}

inline void Racional::lê()
{
    ...
}

inline Racional& Racional::operator++()
{
    ...
}

inline Racional& Racional::operator--()
{
    ...
}

inline Racional& Racional::operator*=(Racional const& r2)
{
    ...
}

inline Racional& Racional::operator/=(Racional const& r2)
{
    ...
}

inline Racional& Racional::operator+=(Racional const& r2)
{
    assert(cumpreInvariante() and r2.cumpreInvariante());

    numerador_ = numerador_ * r2.denominador_ +
        r2.numerador_ * denominador_;
    denominador_ *= r2.denominador_;

    reduz();

    assert(cumpreInvariante());

    return *this;
}

inline Racional& Racional::operator-=(Racional const& r2)
{
    ...
}

inline void Racional::reduz()
{
    assert(denominador_ != 0);

    int divisor = mdc(numerador_, denominador_);

    numerador_ /= divisor;
    denominador_ /= divisor;

    assert(denominador_ != 0 and mdc(numerador_, denominador_) == 1);
}

inline bool Racional::cumpreInvariante()
{
    ...
}

/** Produto de dois racionais.
    @pre V.
    @post operator* = r1 × r2. */
inline Racional const operator*(Racional r1, Racional const& r2)
{
    ...
}

/** Divisão de dois racionais.
    @pre r2 <> 0.
    @post operator/ = r1 / r2. */
inline Racional const operator/(Racional r1, Racional const& r2)
{
    ...
}

/** Soma de dois racionais.
    @pre V.
    @post operator+ = r1 + r2. */
inline Racional const operator+(Racional r1, Racional const& r2)
{
    return r1 += r2;
}

/** Subtracção de dois racionais.
    @pre V.
    @post operator- = r1 - r2. */
inline Racional const operator-(Racional r1, Racional const& r2)
{
    ...
}

/** Devolve verdadeiro se dois racionais forem iguais.
    @pre V.
    @post operator== = (r1 = r2). */
inline bool operator==(Racional const& r1, Racional const& r2)
{
    return r1.numerador() == r2.numerador() and
           r1.denominador() == r2.denominador();
}

/** Devolve verdadeiro se dois racionais forem iguais.
    @pre V.
    @post operator != = (r1 <> r2). */
inline bool operator!=(Racional const& r1, Racional const& r2)
{
    ...
}

int main()
{
    ...
}

Se houver tempo:

Ficaram a faltar...

++, -- sufixo
+, - unários
<, <=, >, >=

e ainda

<< e >> para inserção e extracção em e de canais

Vamos definir primeiro os operadores de incrementação e decrementação sufixo.  

Discutir com eles que têm o mesmo número de operandos que os prefixo.  Como os distinguir?

Distinguem-se de uma forma simples e eficiente, embora muito, muito feia...  Basta dizer que têm um parâmetro adicional do tipo int!

Assim, se forem definidos fora da classe C++ terão o aspecto:

Racional const operator++(Racional& r, int);

e se forem definidos dentro da classe C++, como membros,

Racional const Racional::operator++(int);

Vamos defini-los como não-membros da classe C++:

/** Incrementa o racional, devolvendo o seu valor antes de incrementado.
    @pre r = r.
    @post operator++ = r e r = r + 1. */
inline Racional const operator++(Racional& r, int)
{
    Racional copia = r;
    ++r;

    return copia;
}

/** Decrementa o racional, devolvendo o seu valor antes de decrementado.
    @pre r = r.
    @post operator-- = r e r = r - 1. */
inline Racional const operator--(Racional& r, int)
{
    Racional copia = r;
    --r;

    return copia;
}

Chamo a atenção para o facto de os operadores fazerem logicamente parte do TAD, mesmo não pertencendo à classe C++ que o implementa!

E os operadores + e - unários?  São simples:

/** Representa números racionais.  
    @invariant 0 < denominador_ e mdc(numerador_, denominador_) = 1. */
class Racional {
  public:

    ...

    /** Devolve simétrico do racional.
        @pre V.
        @post operator- = -*this. */
    Racional const operator-() const;

    ...

};

...

inline Racional const Racional::operator-() const
{
    assert(cumpreInvariante());

    Racional r;

    r.numerador_ = -numerador_;
    r.denominador_ = denominador_;

    assert(r.cumpreInvariante());

    return r;
}

/** Devolve o racional.
    @pre V.
    @post operator+ idêntico a r. */
inline Racional const& operator+(Racional const& r)
{
    return r;
}

...

Explicar porque se definiu o operador simétrico como membro!  (Por razões de eficiência, pois evitam-se tentativas de redução do racional.)

Finalmente falta definir os operadores relacionais.  Comecemos pelo operador <.  Fá-lo-emos não-membro pela mesma razão que o operador == também o é.

/** Devolve verdadeiro se o primeiro racional for menor que o segundo.
    @pre V.
    @post operator< = r1 < r2. */
inline bool operator<(Racional const& r1, Racional const& r2)
{
    return r1.numerador() * r2.denominador() < 
           r2.numerador() * r1.denominador();
}

Os restantes são fáceis de definir à custa deste!  

Discutir!

/** Devolve verdadeiro se o primeiro racional for maior que o segundo.
    @pre V.
    @post operator< = r1 > r2. */
inline bool operator>(Racional const& r1, Racional const& r2)
{
    return r2 < r1;
}

/** Devolve verdadeiro se o primeiro racional for menor ou igual ao segundo.
    @pre V.
    @post operator< = r1 <= r2. */
inline bool operator<=(Racional const& r1, Racional const& r2)
{
    return not (r1 > r2);
}

/** Devolve verdadeiro se o primeiro racional for maior ou igual ao segundo.
    @pre V.
    @post operator< = r1 >= r2. */
inline bool operator>=(Racional const& r1, Racional const& r2)
{
    return not (r1 < r2);
}

Curiosamente também é possível definir os operadores igual e diferente à custa do operador menor!  Fica como exercício!

Os operadores de inserção e extracção de um canal ficam também como exercício.

O código como está não funciona.  Por exemplo, o operador /= usa o operador != declarado e definido mais tarde.  O ideal neste caso será agrupar as declarações das rotinas do TAD que são externas à classe C++ junto a essa mesma classe:

#include <iostream>
#include <cassert>

using namespace std;

/** Devolve o máximo divisor comum dos inteiros passados como argumento.
    @pre m <> 0 ou n <> 0.
    @post mdc = mdc(m, n). */
int mdc(int const m, int const n) 
{
    assert(m != 0 or n != 0);

    ...
}

/** Representa números racionais.  
    @invariant 0 < denominador_ e mdc(numerador_, denominador_) = 1. */
class Racional {
  public:
    /** Constrói racional com valor inteiro.
        @pre V.
        @post *this = valor. */
    Racional(int const valor = 0);

    /** Constrói racional correspondente a n/d.
        @pre d <> 0.
        @post *this = numerador/denominador. */
    Racional(int const numerador, int const denominador);

    /** Devolve numerador da fracção mínima correspondente ao racional.
        @pre V.
        @post numerador /denominador() = *this. */
    int numerador();

    /** Devolve denominador da fracção mínima correspondente ao racional.
        @pre V.
        @post (E n : : n/denominador = *this e 0 < denominador e
              mdc(n, denominador) = 1). */
    int denominador();

    /** Escreve um racional no ecrã no formato de uma fracção.
        @pre V.
        @post ¬cout.good() ou cout contém n/d  (ou simplesmente
              n, se d = 1) em que n e d são os valores de numerador() e denominador(). */
    void escreve();

    /** Devolve simétrico do racional.
        @pre V.
        @post operator- = -*this. */
    Racional const operator-() const;

    /** Lê do teclado o racional, na forma de dois inteiros sucessivos.
        @pre *this = r.
        @post Se cin.good() e cin tem dois inteiros n' e d' disponíveis para
              leitura, com d' <> 0,
              então *this = n'/d',
              senão *this = r e ¬cin.good(). */
    void lê();

    /** Incrementa o racional.
        @pre *this = r.
        @post operator++ idêntico a *this e *this = r + 1. */
    Racional& operator++();

    /** Decrementa o racional.
        @pre *this = r.
        @post operator-- idêntico a *this e *this = r - 1. */
    Racional& operator--();

    /** Multiplica por um racional.
        @pre *this = r.
        @post operator*= idêntico a *this e *this = r × r2. */
    Racional& operator*=(Racional const& r2);

    /** Divide por um racional.
        @pre *this = r e r2 <> 0.
        @post operator/= idêntico a *this e *this = r / r2. */
    Racional& operator/=(Racional const& r2);

    /** Adiciona de um racional.
        @pre *this = r.
        @post operator+= idêntico a *this e *this = r + r2. */
    Racional& operator +=(Racional const& r2);

    /** Subtrai de um racional.
        @pre *this = r.
        @post operator-= idêntico a *this e *this = r - r2. */
    Racional& operator-=(Racional const& r2);

  private:
    int numerador_;
    int denominador_;

    /** Reduz a fracção que representa o racional.
        @pre denominador_ <> 0 e *this = r.
        @post denominador_ <> 0 e mdc(numerador_, denominador_) = 1 e
            *this = r. */
    void reduz();

    /** Indica se a CIC se verifica.
        @pre V.
        @post cumpreInvariante = 0 < denominador_ e mdc(numerador_, denominador_) = 1. */
    bool cumpreInvariante() const;
};

/** Incrementa o racional, devolvendo o seu valor antes de incrementado.
    @pre r = r.
    @post operator++ = r e r = r + 1. */
inline Racional const operator++(Racional& r, int);

/** Decrementa o racional, devolvendo o seu valor antes de decrementado.
    @pre r = r.
    @post operator-- = r e r = r - 1. */
inline Racional const operator--(Racional& r, int);

/** Produto de dois racionais.
    @pre V.
    @post operator* = r1 × r2. */
Racional const operator*(Racional r1, Racional const& r2);

/** Divisão de dois racionais.
    @pre r2 <> 0.
    @post operator/ = r1 / r2. */
Racional const operator/(Racional r1, Racional const& r2);

/** Soma de dois racionais.
    @pre V.
    @post operator+ = r1 + r2. */
Racional const operator+(Racional r1, Racional const& r2);

/** Subtracção de dois racionais.
    @pre V.
    @post operator- = r1 - r2. */
Racional const operator-(Racional r1, Racional const& r2);

/** Devolve o racional.
    @pre V.
    @post operator+ idêntico a r. */
inline Racional const& operator+(Racional const& r);

/** Devolve verdadeiro se dois racionais forem iguais.
    @pre V.
    @post operator== = (r1 = r2). */
bool operator==(Racional const& r1, Racional const& r2);

/** Devolve verdadeiro se dois racionais forem iguais.
    @pre V.
    @post operator != = (r1 <> r2). */
bool operator!=(Racional const& r1, Racional const& r2);

/** Devolve verdadeiro se o primeiro racional for menor que o segundo.
    @pre V.
    @post operator< = r1 < r2. */
inline bool operator<(Racional const& r1, Racional const& r2);

/** Devolve verdadeiro se o primeiro racional for maior que o segundo.
    @pre V.
    @post operator< = r1 > r2. */
inline bool operator>(Racional const& r1, Racional const& r2);

/** Devolve verdadeiro se o primeiro racional for menor ou igual ao segundo.
    @pre V.
    @post operator< = r1 <= r2. */
inline bool operator<=(Racional const& r1, Racional const& r2);

/** Devolve verdadeiro se o primeiro racional for maior ou igual ao segundo.
    @pre V.
    @post operator< = r1 >= r2. */
inline bool operator>=(Racional const& r1, Racional const& r2);

inline Racional::Racional(int const valor)
    : numerador_(valor), denominador_(1)
{
    ...
}

inline Racional::Racional(int const numerador, int const denominador) 
{
    ...
}

inline int Racional::numerador()
{
    ...
}

inline int Racional::denominador()
{
    ...
}

inline void Racional::escreve()
{
    ...
}

inline Racional const Racional::operator-() const
{
    ...
}

void Racional::lê()
{
    ...
}

inline Racional& Racional::operator++()
{
    ...
}

inline Racional& Racional::operator--()
{
    ...
}

inline Racional& Racional::operator*=(Racional const& r2)
{
    ...
}

inline Racional& Racional::operator/=(Racional const& r2)
{
    ...
}

inline Racional& Racional::operator+=(Racional const& r2)
{
    ...
}

inline Racional& Racional::operator-=(Racional const& r2)
{
    ...
}

inline inline void Racional::reduz()
{
    ...
}

inline bool Racional::cumpreInvariante()
{
    ...
}

inline Racional const operator++(Racional& r, int)
{
    ...
}

inline Racional const operator--(Racional& r, int)
{
    ...
}

inline Racional const operator*(Racional r1, Racional const& r2)
{
    ...
}

inline Racional const operator/(Racional r1, Racional const& r2)
{
    ...
}

inline Racional const operator+(Racional r1, Racional const& r2)
{
    ...
}

inline Racional const operator-(Racional r1, Racional const& r2)
{
    ...
}

inline Racional const& operator+(Racional const& r)
{
    ...
}

inline bool operator==(Racional const& r1, Racional const& r2)
{
    ...
}

inline bool operator!=(Racional const& r1, Racional const& r2)
{
    ...
}

inline bool operator<(Racional const& r1, Racional const& r2)
{
    ...
}

inline bool operator>(Racional const& r1, Racional const& r2)
{
    ...
}

inline bool operator<=(Racional const& r1, Racional const& r2)
{
    ...
}

inline bool operator>=(Racional const& r1, Racional const& r2)
{
    ...
}

int main()
{
    ...
}

#ifdef TESTE

int main()
{
    assert(mdc(10, 0) == 10);
    assert(mdc(0, 10) == 10);
    assert(mdc(10, 10) == 10);
    assert(mdc(3, 7) == 1);
    assert(mdc(8, 6) == 2);
    assert(mdc(-8, 6) == 2);
    assert(mdc(8, -6) == 2);
    assert(mdc(-8, -6) == 2);

    Racional r1(2, -6);

    assert(r1.numerador() == -1 and r1.denominador() == 3);

    Racional r2(3);

    assert(r2.numerador() == 3 and r2.denominador() == 1);

    Racional r3;

    assert(r2 == 3);
    assert(3 == r2);
    assert(r3 == 0);
    assert(0 == r3);

    assert(r1 < r2);
    assert(r2 > r1);
    assert(r1 <= r2);
    assert(r2 >= r1);
    assert(r1 <= r1);
    assert(r2 >= r2);

    assert(r2 == +r2);
    assert(-r1 == Racional(1, 3));

    assert(++r1 == Racional(2, 3));
    assert(r1 == Racional(2, 3));

    assert(r1++ == Racional(2, 3));
    assert(r1 == Racional(5, 3));

    assert((r1 *= Racional(7, 20)) == Racional(7, 12));
    assert((r1 /= Racional(3, 4)) == Racional(7, 9));
    assert((r1 += Racional(11, 6)) == Racional(47, 18));
    assert((r1 -= Racional(2, 18)) == Racional(5, 2));

    assert(r1 + r2 == Racional(11, 2));
    assert(r1 - Racional(5, 7) == Racional(25, 14));
    assert(r1 * 40 == 100);
    assert(30 / r1 == 12);
 }

#endif // TESTE

Este código já tem o respectivo teste de unidade.  Faltam apenas os operadores de inserção e extracção de canais.  Ver código no directório de código!