Problema

Traçador de gráficos de funções

Sumário

• Objectivos
  • Estrutura geral
  • Funcionamento do traçador de gráficos
  • Definição da função matemática a representar
  • Validação das entradas de dados
  • Exemplo de interacção
  • Extras
• Módulos a desenvolver
• Requisitos
• Resolução e entrega

1  Objectivos

O objectivo deste problema é implementar um programa para traçar gráficos de funções.

1.1  Estrutura geral

O programa permite ao utilizador traçar um número indeterminado de gráficos de determinada função real de variável real.  Para traçar um gráfico, o utilizador deve escolher os limites do intervalo do eixo das abcissas (X) em que a função deve ser representada e um incremento que indica para que valores das abcissas devem ser calculados os valores do eixo das ordenadas (Y) a representar.  Após a exibição do gráfico deve ser possível traçar um novo gráfico ou sair do programa.

1.2  Funcionamento do traçador de gráficos

Quando o programa se inicia, deve ser exibido o seguinte menu:

Traçador de gráficos

Menu principal

1. Traçar gráfico
2. Sair

Opção: 

O utilizador tem, então, a possibilidade de escolher uma das duas opções apresentadas.

Caso a opção 1 seja escolhida, o computador deve perguntar ao utilizador os limites do intervalo a representar.

Introduza o limite inferior do intervalo: 0.0
Introduza o limite superior do intervalo: 12.0

Depois da introdução dos limites do intervalo, o computador deve perguntar ao utilizador qual o incremento que deverá utilizar para percorrer o intervalo.

Introduza o incremento: 0.5

Após a leitura desta informação, o computador deve traçar o gráfico de uma função pré-definida. Por exemplo, se essa função for

f(x) = 15 × sen(x)

no ecrã deverá surgir algo como:

               0
|----|----|----|----|----|----|
               -                f(0) = 0
               |*******         f(0.5) = 7.19138
               -*************   f(1) = 12.6221
               |*************** f(1.5) = 14.9624
               -**************  f(2) = 13.6395
               |*********       f(2.5) = 8.97708
               -**              f(3) = 2.1168
          *****|                f(3.5) = -5.26175
    ***********-                f(4) = -11.352
***************|                f(4.5) = -14.663
 **************-                f(5) = -14.3839
    ***********|                f(5.5) = -10.5831
           ****-                f(6) = -4.19123
               |***             f(6.5) = 3.2268
               -**********      f(7) = 9.8548
               |**************  f(7.5) = 14.07
               -*************** f(8) = 14.8404
               |************    f(8.5) = 11.9773
               -******          f(9) = 6.18178
              *|                f(9.5) = -1.12727
       ********-                f(10) = -8.16032
  *************|                f(10.5) = -13.1954
***************-                f(11) = -14.9999
  *************|                f(11.5) = -13.1318
       ********-                f(12) = -8.04859


Isto é, o gráfico da função f(x) rodado 90º, sendo os valores de f(x) apresentados à frente da sua representação.

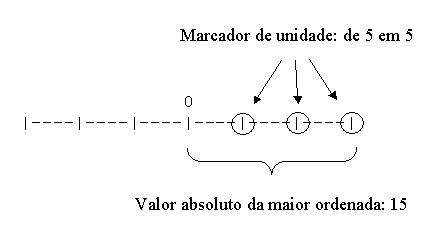
Caso os valores de f(x) sejam maiores que o valor absoluto da maior ordenada representável, cujo valor é 15 (a marcação das unidades é de 5 em 5), a sua representação deve ser limitada pelo valor absoluto da maior ordenada representável.  Por exemplo, se, usando a função anterior, o valor absoluto da maior ordenada representável fosse 10, o gráfico de f(x) teria o seguinte aspecto:

          0
|----|----|----|----|
          -           f(0) = 0
          |*******    f(0.5) = 7.19138
          -********** f(1) = 12.6221
          |********** f(1.5) = 14.9624
          -********** f(2) = 13.6395
          |*********  f(2.5) = 8.97708
          -**         f(3) = 2.1168
     *****|           f(3.5) = -5.26175
**********-           f(4) = -11.352
**********|           f(4.5) = -14.663
**********-           f(5) = -14.3839
**********|           f(5.5) = -10.5831
      ****-           f(6) = -4.19123
          |***        f(6.5) = 3.2268
          -********** f(7) = 9.8548
          |********** f(7.5) = 14.07
          -********** f(8) = 14.8404
          |********** f(8.5) = 11.9773
          -******     f(9) = 6.18178
         *|           f(9.5) = -1.12727
  ********-           f(10) = -8.16032
**********|           f(10.5) = -13.1954
**********-           f(11) = -14.9999
**********|           f(11.5) = -13.1318
  ********-           f(12) = -8.04859


Terminado o traçado do gráfico da função, o programa deve voltar a exibir o menu principal.

Caso seja escolhida a opção 2, o programa deve terminar.

1.3  Definição da função matemática a representar

A função matemática a representar deve ser implementada como um módulo do programa.  Ou seja, caso se pretenda traçar o gráfico da função f(x) = 15 × sen(x), deve definir-se a seguinte função C++ no programa:

#include <iostream>
#include <cmath>

using namespace std;

...

/** Devolve 15 × sen(x).
    @pre V.
    @post f = 15 × sen(x). */
double f(double const x)
{
    return 15.0 * sin(x);
}

...

int main()
{

    ...

}

A parte do código que calcula o valor a representar deve invocar esta função.  Sempre que se pretender alterar a função matemática cujo gráfico é traçado pelo programa deve alterar-se no programa a implementação da função double f(double const x).

1.4  Validação das entradas de dados

De modo a garantir o bom funcionamento do programa, devem validar-se as entradas de dados.  Assim existem as seguintes verificações a realizar:

• A opção introduzida pelo utilizador após a exibição do menu principal deve ser um número inteiro que pode apenas tomar os valores 1 e 2.  Deve verificar-se se o inteiro introduzido pertence a este conjunto.  Caso tal não aconteça, o computador deve pedir uma nova opção.
• O valor do limite inferior do intervalo a representar deve ser menor que o valor do limite superior desse intervalo.  Caso tal não aconteca, o computador deve voltar a perguntar quais os limites do intervalo.
• O incremento deve ser um valor positivo.  Se o utilizador introduzir um valor negativo ou zero, o incremento deve ser pedido novamente.

Não é necessário validar os tipos dos valores: se for pedido um valor inteiro, assume-se que o utilizador introduz um valor inteiro; se for pedido um valor decimal, assume-se que o utilizador introduz um valor decimal.

1.5  Exemplo de interacção

Abaixo mostra-se uma possível interacção entre o programa e o utilizador.  A função utilizada é a referida anteriormente, i.e., f(x) = 15 × sen(x).  A negrito encontram-se as respostas do utilizador do programa:

Traçador de gráficos

Menu principal

1. Traçar gráfico
2. Sair

Opção: 1

 

Introduza o limite inferior do intervalo: 0.0
Introduza o limite superior do intervalo: 12.0

Introduza o incremento: 0.5

Gráfico de f(x):

               0
|----|----|----|----|----|----|
               -                f(0) = 0
               |*******         f(0.5) = 7.19138
               -*************   f(1) = 12.6221
               |*************** f(1.5) = 14.9624
               -**************  f(2) = 13.6395
               |*********       f(2.5) = 8.97708
               -**              f(3) = 2.1168
          *****|                f(3.5) = -5.26175
    ***********-                f(4) = -11.352
***************|                f(4.5) = -14.663
  **************-                f(5) = -14.3839
    ***********|                f(5.5) = -10.5831
           ****-                f(6) = -4.19123
               |***             f(6.5) = 3.2268
               -**********      f(7) = 9.8548
               |**************  f(7.5) = 14.07
               -*************** f(8) = 14.8404
               |************    f(8.5) = 11.9773
               -******          f(9) = 6.18178
              *|                f(9.5) = -1.12727
       ********-                f(10) = -8.16032
  *************|                f(10.5) = -13.1954
***************-                f(11) = -14.9999
  *************|                f(11.5) = -13.1318
       ********-                f(12) = -8.04859


 

Traçador de gráficos

Menu principal

1. Traçar gráfico
2. Sair

Opção: 3

Opção inválida!

Opção: 1

 

Introduza o limite inferior do intervalo: 12.0
Introduza o limite superior do intervalo: 0.0

O valor do limite inferior é maior que o valor do limite superior.

Introduza o limite inferior do intervalo: 0.0
Introduza o limite superior do intervalo: 5.0

Introduza o incremento: -0.5

O valor do incremento deve ser positivo.

Introduza o incremento: 0.5

Gráfico de f(x):

               0
|----|----|----|----|----|----|
               -                f(0) = 0
               |*******         f(0.5) = 7.19138
               -*************   f(1) = 12.6221
               |*************** f(1.5) = 14.9624
               -**************  f(2) = 13.6395
               |*********       f(2.5) = 8.97708
               -**              f(3) = 2.1168
          *****|                f(3.5) = -5.26175
    ***********-                f(4) = -11.352
***************|                f(4.5) = -14.663
  **************-                f(5) = -14.3839

 

Traçador de gráficos

Menu principal

1. Traçar gráfico
2. Sair

Opção: 2

Até breve!

1.6  Extras

Os alunos são livres de melhorar o programa da forma que entenderem, desde que não o desvirtuem.  Estas melhorias não terão, por si só, influência na nota.  A qualidade da programação é o ponto essencial.

Sugestão

Em C++, as rotinas podem ter outras rotinas como parâmetros.  Uma melhoria interessante poderá ser acrescentar ao programa a implementação de várias funções matemáticas. Deste modo, a escolha da opção "Traçar gráfico" teria como consequência a exibição de um menu com as funções que é possivel representar.  O utilizador poderia, então, escolher qualquer uma, sem que fosse necessário modificar o código e gerar novo executável para traçar o seu gráfico.

Abaixo pode encontrar, a título ilustrativo, um procedimento que tem como objectivo mostrar no ecrã uma tabela de uma função matemática real de variável real recebida como parâmetro.

/** Devolve 15 × sen(x).
    @pre V.
    @post f = 15 × sen(x). */
double f(double const x)
{
    return 15.0 * sin(x);
}

/** Mostra no ecrã a tabela de valores de f(), desde limite_inferior até
    limite_superior, com incremento incremento.
    @pre limite_inferior <= limite_superior e
          0 < incremento.
    @post O ecrã contém a tabela de f() desde limite_inferior até
           limite_superior, com incremento incremento. */
void mostraTabela(double f(double), double const limite_inferior,
                                    double const limite_superior,
                                    double const incremento)
{
    assert(limite_inferior <= limite_superior and 0 < incremento);

    ...
}

2  Módulos a desenvolver

O programa a desenvolver deve conter, pelo menos, os seguintes módulos:

• Módulo responsável pelo arredondamento de valores decimais.  Deve calcular e devolver o inteiro mais próximo.
• Módulo responsável pelo desenho de um segmento horizontal constituído por n cópias do caractere a utilizar no desenho do segmento.  Tem como parâmetros o caractere a utilizar no desenho do segmento e o tamanho que o segmento deve ter, ou seja, o número de cópias do caractere a desenhar.
• Módulo responsável pelo desenho do eixo das ordenadas.  O eixo é composto por duas linhas: na primeira linha deve apenas aparecer o valor zero, como valor central do eixo; na segunda linha aparece o eixo propriamente dito.  O valor absoluto da maior ordenada representável é 15.  A marcação das unidades no eixo das ordenadas é de 5 em 5.

• Módulo responsável pelo desenho do eixo das abcissas.  Deve decidir e escrever no ecrã o caractere relativo ao eixo das abcissas, dado o valor de x.  Caso x não tenha parte decimal, o caractere a usar é '-', caso contrário deve ser usado o caractere '|'.
• Módulo responsável pela representação do par (x, f(x)).  Este módulo recebe como argumentos os valores de x e f(x) e deve representá-los no ecrã.
• Módulo responsável pelo desenho do gráfico da função no intervalo dado.  Tem como parâmentros o limite inferior do intervalo, o limite superior do intervalo e o incremento.
• Módulo com a implementação da função matemática f(x) = 15 × sen(3 × x) × e^{-x / 10}.

3  Requisitos

A resolução deverá cumprir os seguintes requisitos:

1. Estruturação apropriada.  I.e., modularização apropriada em rotinas (funções e procedimentos).
2. Nomes de entidades (variáveis, constantes e rotinas) apropriados.
3. Documentação apropriada.  Todas as rotinas deverão ser documentadas.
4. Programação por contrato.  Todas as rotinas deverão, se possível e necessário, conter asserções explicitando pré-condições e condições objectivo.
5. Todas as opções importantes e/ou extras do programa deverão ser explicados num pequeno texto de no máximo uma página A4 integrado no relatório.

4  Resolução e entrega

• Os casos omissos neste enunciado deverão ser esclarecidos junto de um dos docentes da disciplina.
• Resolvido em grupo (ver página da disciplina).
• Resolução entregue pessoalmente a um dos docentes da disciplina até às 17:30h do dia 15 de Novembro de 2002.
• Resolução entregue em disquete, devidamente identificada, contendo apenas o ficheiro onde se encontra o código, acompanhada por um relatório com uma listagem dos ficheiros fonte (contendo código C++).  Use o modelo fornecido: Word, ou RTF.  Deve também enviar uma mensagem de correio electrónico com o ficheiro de código (.C) para Ricardo.Ribeiro@iscte.pt.  O assunto (subject) desta mensagem deve ser exactamente <Problema de IP> (com o menor inicial e o maior final).  Todas as mensagens cujo assunto não seja exactamente igual ao referido serão descartadas.
• Imprima o código em C++ sempre de uma forma bem legível: use sempre um tipo não proporcional (e.g., Courier ou Lucida Console) e, caso seja possível fazê-lo, imprima em papel reciclado, frente-e-verso.
• A não observação dos modos de entrega descritos acima poderá ser penalizada.
• A entrega de resoluções fora do prazo implica a penalização de dois (2) valores por dia útil de atraso, não se aceitando resoluções entregues com mais do que 5 dias úteis de atraso (i.e., depois das 17:30h de dia 22 de Novembro de 2002).
• Exija ao docente a entrega de um recibo comprovativo da entrega do trabalho.  Este recibo é a única prova que tem da entrega do seu trabalho.