Trabalho de Programação II e Programação Orientada para Objectos 1998/1999

Notas

A resolver em grupo.
Leia atentamente todo o enunciado.
Se o julgar conveniente, peça ao seu delegado de turma para marcar junto dos docentes da disciplina uma sessão de explicações sobre o trabalho.
A resolução deste trabalho deve ser entregue até ao dia 4 de Junho de 1999. A resolução deve ser entregue pessoalmente a um dos docentes da cadeira e consta de uma disquete, devidamente identificada e contendo apenas os ficheiros onde se encontra o código (e o projecto), e ainda de um pequeno relatório, com um máximo de duas páginas, em modelo a fornecer brevemente.
A entrega do trabalho fora do prazo implica a penalização de um valor por cada dia útil de atraso (i.e., 5, 6 ou 7 de Junho, -1 valor; 8 de Junho -2 valores; 9 de Junho -3 valores; 10 ou 11 de Junho -4 valores) não se aceitando trabalhos após sexta-feira, 11 de Junho de 1999.

1 Objectivo

O objectivo deste trabalho é desenvolver um sistema de planificação e orçamentação de projectos de obra (em construção civil) muito simplificado.

Um projecto de obra consiste num conjunto de tarefas, que podem ser de tipos diferentes. Cada tarefa tem sempre uma duração, em número de dias, uma necessidade de mão de obra, em número de operários (que, para se simplificar, se considera indiferenciada, i.e., os operários são todos generalistas, sabem fazer tudo), um custo de material e um custo de mão de obra. As tarefas podem depender de outras tarefas. Por exemplo, se existirem as tarefas A, B e C correspondentes a construção de fundações, construção de paredes e instalação de cabos eléctricos, então a tarefa B só pode ser realizada depois da tarefa A e a tarefa C depois da B. Diz-se, neste caso, que B é sucessora de A e predecessora de C e que C é sucessora de B. Ou ainda que B depende de A e C depende de B.

O planeamento dum projecto corresponte a dizer:

que tarefas são realizadas quando,
quanto tempo demorará o projecto a ser executado, e
quais os recursos necessários em termos de mão de obra em cada instante de tempo.

O programa proporcionará ferramentas para optimização da duração dum projecto e ferramentas para auxílio na optimização dos recursos humanos necessários num projecto.

A orçamentação corresponde a listar discriminadamente os custos dos materiais e da mão de obra utilizada.

1.1 Mão de obra

A informação sobre a mão de obra necessária num projecto inclui dois itens. O primeiro é o número máximo de operários necessários em simultâneo em algum ponto da execução do projecto de acordo com o seu planeamento. O segundo é a mão de obra total em termos de operários dia, e só depende das tarefas, sendo portanto independente do planeamento.

Admite-se que a empresa que realizará a obra de construção pode contratar e despedir operários sempre que lhe apetecer e sem quaisquer custos (não é possível nem desejável na prática, mas simplifica a construção do programa...). Admite-se ainda que um operário é pago ao dia, mesmo que só precise de trabalhar umas horas ou uns minutos.

1.2 Tarefas

Para todas as tarefas, independentemente do seu tipo efectivo, deve ser possível saber qual a duração, o número de operários necessários em simultâneo para a concretizar, o custo total da mão de obra e o custo total do material. Claro está que estes valores dependem dos parâmetros de cada tipo de tarefa, conforme se indica abaixo. Também deverá ser possível obter uma descrição da tarefa, do material e ainda notas várias sobre a tarefa.

Admitem-se pelo menos quatro tipos da tarefas: tarefas orçamentadas por área, tarefas orçamentadas por dimensão linear, tarefas orçamentadas à peça e tarefas unitárias. Estes tipos podem ser expandidos ou especializados a gosto, embora tal não seja exigido.

As tarefas não são fragmentáveis. I.e., se a tarefa consiste em pintar 100 m² de parede, só o utilizador do programa poderá fragmentar a tarefa em duas (e.g., de 50 m²).

O Problema 4 da avaliação periódica incidirá sobre a representação das tarefas através de uma hierarquia de classes em C++ usando polimorfismo.

1.2.1 Tarefas orçamentadas por área

São tarefas tais como a pintura, a picagem de paredes, assentamento de pavimentos, etc. Estas tarefas guardarão informação sobre:

Área intervencionada, em m², [a] (e.g., há que pintar 1 000 m² de parede).
Número de operários atribuídos [o] (e.g., a tarefa será realizada por 3 operários).
Tempo, em dias, gasto por um operário por cada m² [e] (e.g., um operário gasta 1/100 dias de trabalho para pintar 1m², ou, o que é o mesmo, pinta 100m² por dia).
Custo, em escudos, da mão de obra por dia [cmo] (e.g., um operário cobra 8 000$ por dia para pintar).
Custo do material por m² [cmat] (e.g., a tinta custa 500$ por m²).
Descrição da tarefa (e.g., "Pintura das paredes exteriores").
Descrição do material (e.g., "Tinta CIN 1234").
Notas várias (e.g., "Aplicar 4 demãos").

Com esta informação, é fácil calcular:

Duração: dur = [e × a / o] (ou seja, [1/100 × 1 000 / 3] = 4 dias).
Custo do material: Cmat = a × cmat (ou seja, 1 000 × 500 = 500 000$).
Custo da mão de obra: Cmo = o cmo dur (ou seja, 3 × 8 000 × 4 = 96 000$).

Onde [x] significa o inteiro mais pequeno não inferior a x.

1.2.2 Tarefas orçamentadas por dimensão linear

São tarefas tais como a instalação de rodapés, montagem de canalização, instalação de cabos eléctricos, etc. Estas tarefas guardarão informação sobre:

Dimensão intervencionada, em m, [l] (e.g., há que instalar 120 m de rodapés).
Número de operários atribuídos [o] (e.g., a tarefa será realizada por 2 operários).
Tempo, em dias, gasto por um operário por cada m [e] (e.g., um operário gasta 1/100 dias de trabalho para instalar 1m de rodapé, ou seja, instala 100 m de rodapé por dia).
Custo, em escudos, da mão de obra por dia [cmo] (e.g., um operário cobra 7 000$ por dia para instalar rodapés).
Custo do material por m [cmat] (e.g., os rodapés custam 200$ cada m).
Descrição da tarefa (e.g., "Instalação dos rodapés").
Descrição do material (e.g., "Ripa de pinho").
Notas várias (e.g., "Aparafusar").

Com esta informação, é fácil calcular:

Duração: dur = [e × l / o] (ou seja, [1/100 × 120 / 2] = 1 dia).
Custo do material: Cmat = l × cmat (ou seja, 120 × 200 = 24 000$).
Custo da mão de obra: Cmo = o cmo dur (ou seja, 2 × 7 000 × 1 = 14 000$).

Note-se que, no exemplo dado, dois operários durante um dia seriam capazes de instalar 200 m de rodapé, pelo que há aqui um desperdício de recursos. Esse facto não o deve preocupar. A unidade atómica de tempo é o dia. Se se pretendesse menos desperdício de recursos poder-se-ia planear à hora.

1.2.3 Tarefas orçamentadas à peça

São tarefas tais como a instalação de interruptores, pintura de janelas e portas, etc. Estas tarefas guardarão informação sobre:

Número de peças a instalar [n] (e.g., há que instalar 75 interruptores).
Número de operários atribuídos [o] (e.g., a tarefa será realizada por 2 operários).
Tempo, em dias, gasto por um operário por cada peça [e] (e.g., um operário gasta 1/50 dias de trabalho para instalar um interruptor, ou seja, instala 50 interruptores por dia).
Custo, em escudos, da mão de obra por dia [cmo] (e.g., um operário cobra 10 000$ por dia para instalar interruptores).
Custo do material por unidade [cmat] (e.g., os interruptores custam 800$ cada um).
Descrição da tarefa (e.g., "Instalação dos interruptores").
Descrição do material (e.g., "Legrand SB900 branco").
Notas várias (e.g., "-").

Com esta informação, é fácil calcular:

Duração: dur = [e × n / o] (ou seja, [1/50 × 75 / 2] = 1 dias).
Custo do material: Cmat = n × cmat (ou seja, 75 × 800 = 60 000$).
Custo da mão de obra: Cmo = o cmo dur (ou seja, 2 × 10 000 × 1 = 20 000$).

1.2.4 Tarefas unitárias

São tarefas tratadas como um todo, por exemplo, a instalação do ar-condicionado. Para este tipo de tarefa guarda-se informação sobre:

Número de operários atribuídos [o] (e.g., a tarefa será realizada por 4 operários).
Duração da tarefa em dias [dur] (e.g., a instalação dura 3 dias).
Custo, em escudos, da mão de obra por dia [cmo] (e.g., um operário cobra 11 000$ por dia para instalar o ar-condicionado).
Custo do material [Cmat] (e.g., 1 500 000$).
Descrição da tarefa (e.g., "Instalação do ar-condicionado").
Descrição do material (e.g., "Sanyo").
Notas várias (e.g., "-").

Com esta informação, é fácil calcular:

Custo da mão de obra: Cmo = o cmo dur (ou seja, 4 × 11 000 × 3 = 132 000$).

2 Funcionalidades requeridas

O programa permite definir e manipular as tarefas dum projecto de obra, gerando planos e orçamentos para a mesma. Deve ser possível:

Inserir uma nova tarefa, de um dos tipos existentes. Para simplificar a referência às tarefas no plano de obra, o utilizador deve especificar uma etiqueta única para a tarefa (e.g., "A" ou "Pintura1"), que será usada pelo programa para a identificar no futuro. Deve-se garantir que não existem duas tarefas com a mesma etiqueta no planeamento. Deve ser possível especificar um tempo para o início da tarefa.
Remover uma tarefa dada a sua etiqueta, se existir.
Mostrar uma tarefa em pormenor.
Inserir uma dependência entre tarefas, dadas as etiquetas duma tarefa e da tarefa de que ela depende. Deve-se verificar a existência de ambas as tarefas e deve-se verificar se a dependência já existe.
Remover uma dependência entre tarefas, dadas as etiquetas duma tarefa e da tarefa de que ela depende. Deve-se verificar se as tarefas e a dependência existem.
Minimizar tempo de concretização da obra. Para isso o programa deverá estabelecer o plano da obra (i.e., que tarefas devem ser realizadas e quando) de modo a minimizar a sua duração total. Ver mais abaixo para um algoritmo simples e eficiente.
Assinalar impossibilidades de planeamento do projecto. Por exemplo, se o utilizador especificar dependências circulares (e.g., a tarefa A depende da tarefa B e vice-versa), estas dependências devem ser mantidas no sistema, mas o programa deverá avisar o utilizador da existência destas dependências sempre que isso seja relevante.
Alterar tarefa. O utilizador deverá poder alterar qualquer item duma tarefa. O plano deverá ser reajustado de modo a continuar válido (os reajustes devem ser os mínimos indispensáveis).
Adiar ou antecipar tarefa. O utilizador deverá poder adiar ou antecipar qualquer tarefa de qualquer período de tempo. Claro está que o plano deverá ser reajustado de modo a garantir a sua validade depois da alteração. Estas alterações são permitidas ao utilizador, mesmo que impliquem um aumento da duração da obra, para que este possa optimizar os recursos humanos diponíveis. Por exemplo, se o construtor tiver apenas 8 operários e existirem no plano duas tarefas simultâneas exigindo cada uma 5 operários, ele poderá desejar adiar uma das tarefas para evitar esse pico de necessidade de mão de obra.
Atribuir nova data de início. Para alterar o início da obra (é portanto necessário que exista uma data de início da obra por omissão).
Atribuir nova data de fim. Para alterar o fim da obra (só pode ter consequências ao nível das folgas das tarefas).
Mostrar planeamento. Lista as tarefas do projecto mostrando os seus tempos de começo e fim os mais cedo possível, o mais tarde possível, e efectivos, bem como a sua folga, assinalando as tarefas críticas. Mostra ainda as predecessoras de cada tarefa. Note-se que o plano deverá respeitar tanto quanto possível os tempos de início especificados pelo utilizador, mesmo que o plano não fique com a duração ideal. Lembre-se que quem planeia a obra tem outras preocupações (e.g., recursos humanos disponíveis) para além do prazo de conclusão.
Mostrar diagrama de Gantt. Mostra o diagrama de Gantt, indicando para cada dia do plano que tarefas estão a ser executadas, com que recursos humanos e mostrando o total de recursos humanos necessários em cada dia.
Os planeamentos deverão incluir sempre as folgas de cada tarefa (i.e., as margens dentro das quais a tarefa deverá ser iniciada e concluída sem que o prazo de conclusão seja afectado). Estas folgas são úteis para o utilizador, pois permitem-lhe saber até que ponto uma tarefa pode ser adiada ou antecipada sem que isso prolongue o prazo do projecto.
Mostrar orçamento. Mostra uma lista discriminada e pormenorizada de todos os custos do projecto de obra, incluindo custos de mão de obra e de material. Mostra os custos totais.
Escrever projecto em ficheiro. Para guardar os dados inseridos pelo utilizador ao longo duma sessão (o conteúdo anterior do ficheiro é descartado). Ao terminar a execução, o programa deverá avisar o utilizador se este não tiver salvo a informação introduzida.
Ler projecto de ficheiro. Para carregar um projecto guardado anteriormente num ficheiro. O projecto anterior (em memória) é descartado.
Todas as alterações ao projecto devem ser reflectidas no seu planeamento. A filosofia deverá ser sempre a de ajustar apenas as tarefas sucessoras, de modo a não afectar o início do projecto. O início do projecto deverá ser afectado apenas a pedido explícito do utilizador. O fim poderá ser alterado sempre que seja necessário. (Como o planeamento só é mostrado a pedido do utilizador, é vantajoso adiar o planeamento até que ele seja pedido, ver Secção 4.2.)
As tarefas devem ser ordenadas por ordem alfabética de etiqueta para efeitos de visualização.

Devem ser verificados erros a todos os níveis, nomeadamente os de entradas do utilizador.

3 Exemplo de execução

O seguinte exemplo não é exaustivo. Para os casos incluídos, o seu programa deverá apresentar um comportamento idêntico. Nos casos omissos use o bom senso ou pergunte a opinião dos docentes. A negrito encontram-se as respostas do utilizador do programa.

t - nova tarefa.
i - nova tarefa com inicio explícito.
L tarefa - mostra uma tarefa.
a tarefa - altera uma tarefa.
r tarefa - remove uma tarefa.
d nome de - nova dependência.
R nome de - remove dependência.
+ tarefa tempo - adia tarefa.
- tarefa tempo - antecipa tarefa.
< tempo - novo inicio.
> tempo - novo fim.
l - mostra plano tarefa a tarefa.
G - mostra plano em diagrama de Gantt.
m - minimiza projecto.
o - mostra orçamento.
g ficheiro - guarda projecto.
c ficheiro - carrega projecto.
s - sai.
? - ajuda.
> t
Tarefa:
        por área
        à peça
        linear
        unitária
Que tipo de tarefa deseja?
unitária
Descreva a tarefa brevemente: Construção de paredes
Descreva o material: tijolo e cimento
Introduza notas várias: -
Qual a duração da tarefa (em dias)? 15
Quantos operários ocupa? 10
Qual o preço da mão obra por dia e por operário (em escudos)? 3000
Qual o preço total do material (em escudos)? 1000000
Que etiqueta dá à tarefa? A
> t
Tarefa:
        por área
        à peça
        linear
        unitária
Que tipo de tarefa deseja?
linear
Descreva a tarefa brevemente: Abertura de roços
Descreva o material: -
Introduza notas várias: -
Qual o comprimento? 500
Quantos operários ocupa? 2
Quanto tempo dura cada operario por unidade de comprimento (em dias)? 0.02
Qual o preço da mão obra por dia e por operário (em escudos)? 3000
Qual o preço de material por cada unidade de comprimento (em escudos)? 0
Que etiqueta dá à tarefa? B
> L B
Abertura de roços
        duração: 5 dias
                0.02 dias por operario e por unidade de comprimento
        mão de obra: 2 operários
                custo por dia: 3000$
                custo total: 30000$
        material: -
                comprimento: 500
                custo por unidade de comprimento: 0$
                custo total: 0$
        notas: -
> t
Tarefa:
        por área
        à peça
        linear
        unitária
Que tipo de tarefa deseja?
linear
Descreva a tarefa brevemente: Instalação de cabos eléctricos
Descreva o material: Cabelte
Introduza notas várias: -
Qual o comprimento? 1000
Quantos operários ocupa? 2
Quanto tempo dura cada operario por unidade de comprimento (em dias)? 0.002
Qual o preço da mão obra por dia e por operário (em escudos)? 7000
Qual o preço de material por cada unidade de comprimento (em escudos)? 750
Que etiqueta dá à tarefa? C
> L C
Instalação de cabos eléctricos
        duração: 1 dias
                0.002 dias por operario e por unidade de comprimento
        mão de obra: 2 operários
                custo por dia: 7000$
                custo total: 14000$
        material: Cabelte
                comprimento: 1000
                custo por unidade de comprimento: 750$
                custo total: 750000$
        notas: -
> t
Tarefa:
        por área
        à peça
        linear
        unitária
Que tipo de tarefa deseja?
à peça
Descreva a tarefa brevemente: Instalação de tomadas
Descreva o material: Legrand SB 900
Introduza notas várias: -
Qual o número de peças a colocar? 100
Quantos operários ocupa? 2
Quanto tempo dura cada operario a instalar uma peça (em dias)? 0.04
Qual o preço da mão obra por dia e por operário (em escudos)? 7000
Qual o preço de cada peça (em escudos)? 750
Que etiqueta dá à tarefa? D
> L D
Instalação de tomadas
        duração: 2 dias
                0.04 dias por operario e por peça
        mão de obra: 2 operários
                custo por dia: 7000$
                custo total: 28000$
        material: Legrand SB 900
                peças: 100
                custo por peça: 750$
                custo total: 75000$
        notas: -
> t
Tarefa:
        por área
        à peça
        linear
        unitária
Que tipo de tarefa deseja?
por área
Descreva a tarefa brevemente: Pintura de exteriores
Descreva o material: SIN
Introduza notas várias: 3 demãos
Qual a área? 500
Quantos operários ocupa? 2
Quanto tempo dura cada operario por unidade de área (em dias)? 0.01
Qual o preço da mão obra por dia e por operário (em escudos)? 5000
Qual o preço de material por cada unidade de area (em escudos)? 7500
Que etiqueta dá à tarefa? E
> a E
Descrição: Pintura de exteriores
Alterar?
Descrição do material: SIN
Alterar? s
CIN
Notas: 3 demãos
Alterar?
Alterar a área? [500]
Alterar número de operários? [2]
Alterar tempo que cada operario leva por unidade de área? [0.01]
Alterar o preço da mão obra por dia e por operário? [5000$]
Alterar preco do material por unidade de área? [7500$]
> L E
Pintura de exteriores
        duração: 3 dias
                0.01 dias por operario e por unidade de area
        mão de obra: 2 operários
                custo por dia: 5000$
                custo total: 30000$
        material: CIN
                area: 500
                custo por unidade de area: 7500$
                custo total: 3750000$
        notas: 3 demãos
> l
0-15
A(15): 0-15,0-15,0-15: C []
B(5): 0-5,0-5,10-15: 10 []
C(1): 0-1,0-1,14-15: 14 []
D(2): 0-2,0-2,13-15: 13 []
E(3): 0-3,0-3,12-15: 12 []
> d B A
> d C B
> l
0-21
A(15): 0-15,0-15,0-15: C []
B(5): 15-20,15-20,15-20: C [A,]
C(1): 20-21,20-21,20-21: C [B,]
D(2): 0-2,0-2,19-21: 19 []
E(3): 0-3,0-3,18-21: 18 []
> d D c
Erro: Etiqueta c inexistente no projecto!
> d D C
> d E A
> l
0-23
A(15): 0-15,0-15,0-15: C []
B(5): 15-20,15-20,15-20: C [A,]
C(1): 20-21,20-21,20-21: C [B,]
D(2): 21-23,21-23,21-23: C [C,]
E(3): 15-18,15-18,20-23: 5 [A,]
> o
Orçamento da obra.
Items:
0. Construção de paredes:
        mão de obra: 3000$ x 15 dias x 10 operários = 450000$
        material (tijolo e cimento) : 1000000$
1. Abertura de roços:
        mão de obra: 3000$ x 5 dias x 2 operários = 30000$
        material (-) : 500m x 0$ = 0$
2. Instalação de cabos eléctricos:
        mão de obra: 7000$ x 1 dias x 2 operários = 14000$
        material (Cabelte) : 1000m x 750$ = 750000$
3. Instalação de tomadas:
        mão de obra: 7000$ x 2 dias x 2 operários = 28000$
        material (Legrand SB 900) : 100 x 750$ = 75000$
4. Pintura de exteriores:
        mão de obra: 5000$ x 3 dias x 2 operários = 30000$
        material (CIN) : 500m2 x 7500$ = 3750000$
Total material: 5575000$
Total mão de obra: 552000$
Total: 6127000$
> a A
Descrição: Construção de paredes
Alterar?
Descrição do material: tijolo e cimento
Alterar?
Notas: -
Alterar?
Alterar a duração da tarefa? [15 dias]
Alterar o número de operários usados? [10] s
9
Alterar o preço da mão obra por dia e por operário? [3000$]
Alterar o preço total do material? [1000000$]
> o
Orçamento da obra.
Items:
0. Construção de paredes:
        mão de obra: 3000$ x 15 dias x 9 operários = 405000$
        material (tijolo e cimento) : 1000000$
1. Abertura de roços:
        mão de obra: 3000$ x 5 dias x 2 operários = 30000$
        material (-) : 500m x 0$ = 0$
2. Instalação de cabos eléctricos:
        mão de obra: 7000$ x 1 dias x 2 operários = 14000$
        material (Cabelte) : 1000m x 750$ = 750000$
3. Instalação de tomadas:
        mão de obra: 7000$ x 2 dias x 2 operários = 28000$
        material (Legrand SB 900) : 100 x 750$ = 75000$
4. Pintura de exteriores:
        mão de obra: 5000$ x 3 dias x 2 operários = 30000$
        material (CIN) : 500m2 x 7500$ = 3750000$
Total material: 5575000$
Total mão de obra: 507000$
Total: 6082000$
> G
T ABCDE R
----------
0 9.... 9
1 9.... 9
2 9.... 9
3 9.... 9
4 9.... 9
5 9.... 9
6 9.... 9
7 9.... 9
8 9.... 9
9 9.... 9
10 9.... 9
11 9.... 9
12 9.... 9
13 9.... 9
14 9.... 9
15 .2..2 4
16 .2..2 4
17 .2..2 4
18 .2..| 2
19 .2..| 2
20 ..2.| 2
Carregue <enter>
T ABCDE R
----------
21 ...2| 2
22 ...2| 2
> s
Projecto alterado. Guardar? s
Nome do ficheiro: ola

4 Implementação

4.1 Planeamento

Dadas as tarefas a realizar, com a respectiva duração e tempo sugerido de início, e as dependências entre tarefas a considerar, o planeamento consiste em ajustar o início das várias tarefas de modo a que o plano seja consistente, i.e., quaisquer que sejam as tarefas t e s, se s depende de t, então o instante de tempo de início da tarefa s é superior ao instante de tempo de finalização da tarefa t. Admitindo que os tempos são representados por valores inteiros, o fim de uma tarefa pode ser obtido somando a sua duração ao seu instante inicial e subtraindo 1. Por exemplo, se a tarefa t tem início em 2 e dura 4, então termina em 2 + 4 - 1 = 5, pelo que a tarefa s pode ser iniciada a partir de do instante 6.

4.1.1 Diagrama de precedências

À representação de um projecto em que as tarefas correspondem a caixas e as dependências entre tarefas a setas entre essas caixas chama-se "diagrama de precedências". Por exemplo, suponham-se as seguintes tarefas:

Projecto
Tarefas:	Durações:	Depende de:
A	2
B	1	A
C	5	A
D	4	A
E	3	B
F	2	C
G	3	D
H	2	E, F e G
I	2	G
J	3
K	5	J

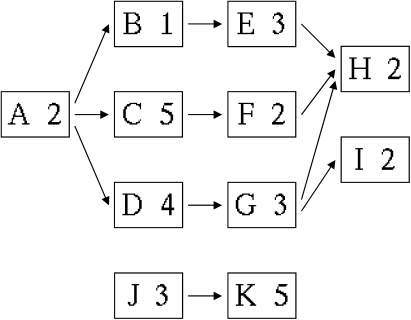
O respectivo diagrama de dependências será:

Diagrama de precedências
Diagrama de dependências

onde se representam as tarefas por caixas com o seu nome e a sua duração e as dependências (ou melhor, as influências) por setas.

4.1.2 Algoritmo de directo de planeamento

Suponha-se que se pretende saber qual a duração mínima do projecto correspondente ao diagrama. Como proceder?

A abordagem deste problema é simples. Pense-se numa dada tarefa, por exemplo H. Do diagrama, é evidente que H é sucessora directa de E, F e G. Mas isso significa que a tarefa H nunca poderá começar antes do final de qualquer uma das tarefas de que depende directamente!

Suponha-se que a primeira tarefa (qualquer que ela seja), dum projecto com o conjunto de tarefas P, tem começo exactamente no instante T_c. Sejam t.c e t.f os tempos de começo e fim o mais cedo possível para a tarefa t pertencente a P. Então o que se afirmou acerca da tarefa H é o mesmo que dizer que H.c = max {E.f, F.f, G.f}. Em geral, sendo t_i, com i = 0, ..., t.n - 1, as t.n predecessoras directas da tarefa t, então

t.c = (M i : 1 <= i < t.n : t_i.f)

(1)

em que (M i : m <= i < n : f(i)) é o quantificador do máximo. I.e., o seu valor é o maior dos valores de f(i) quando i varia na gama de valores dada por m <= i < n. Se a gama de valores possíveis é vazia, então o quantificador não está bem definido.

Mas esta observação ainda não resolve o problema, pois estabelece uma dependência entre as tarefas e as suas predecessoras, mas não diz como calcular os tempos mais cedo de todas as tarefas. É necessário fazer mais algumas observações.

Em primeiro lugar, é preciso notar que a duração total mínima do projecto é a diferença entre o final o mais cedo possível da tarefa que termina mais tarde e o tempo inicial. I.e., o tempo final do projecto é

T_f = (M t : t em P : t.f)

(2)

Em segundo lugar, é necessário validar a equação (1) para o caso em que t.n (o número de predecessoras directas de t) é zero. Nesse caso, que valores pode tomar t.c? Como é óbvio, uma tarefa sem predecessoras pode começar logo no início do projecto, pelo que, quando t.n = 0, tem-se t.c = T_c. Ou seja, a equação deve-se escrever

t.c =	(M i : 1 <= i < t.n : t_i.f)	se t.n <> 0	(3)
	T_c	se t.n = 0	(3)

Então, como qualquer projecto bem construído tem pelo menos uma tarefa sem predecessoras (caso contrário haveria dependências circulares), pode-se começar por atribuir a essas tarefas sem predecessoras como tempo de começo o tempo de começo do projecto. Suponha-se que, para o exemplo acima, o tempo de começo do projecto era 0 (zero). Então, é óbvio que A.c = T_c = 0, A.f = A.c + A.d = 0 + 2 = 2 (sendo t.d a duração da tarefa t), J.c = 0 e J.f = 0 + 3 = 3. Agora é só propagar estes tempos, de acordo com a equação (3), até se processarem todas as tarefas. Mas é necessário transformar estas ideias num algoritmo.

Dado que todas as tarefas terão começo nunca antes do tempo de começo global T_c, comece-se por atribuir esse tempo de começo a todas as tarefas. I.e., faça-se t.c = T_c para todas as tarefas. Associe-se a cada tarefa t um contador t.p (contador das predecessoras directas já processadas), e inicialize-se esse contador com t.n, i.e., com o número de predecessoras directas de t. Coloquem-se as tarefas t tais que t.n = 0 numa fila de espera F. Faça-se:

{O tempo de finalização do projecto ainda não é conhecido:}
T_f <- T_c
{Enquanto a fila de tarefas a processar não estiver vazia:}
enquanto ~ F.vazia() faça-se:
    {Seja t a tarefa à frente da fila. Como as tarefa só são colocadas na fila
     quando as suas predecessoras directas já foram processadas,
     esta tarefa t já tem o valor correcto do tempo de começo mais cedo
     possível t.c:}
    t <- F.frente()
    {Retire-se essa tarefa da fila:}
    F.tira()
    {Calcule-se o tempo de finalização o mais cedo possível da tarefa:}
    t.f <- t.c + t.d
    {Se esse tempo for superior a T_f, então o tempo de finalização do
     projecto tem de ser aumentado:}
    se t.f > T_f
    T_f <- t.f {aumenta-se o mínimo possível.}
    {Agora que já se sabe qual o tempo de finalização mais cedo de t,
     deve-se influenciar o tempo de começo mais cedo das suas sucessoras
     directas:}
    para todas as tarefas s sucessoras directas de t faça-se:
        {Se o tempo de finalização mais cedo de t é superior ao tempo de
         começo mais cedo de s (sucessora de t), então o começo mais
         cedo de s tem de ser aumentado:}
        se s.c < t.f então
           s.c <- t.f
        {Diminua-se o contador de predecessoras já processadas de s,
         pois a tarefa t acabou de ser processada:}
        s.p <- s.p - 1
        {Se o número de predecessoras processadas chegou a zero, então
         s é candidata a ser processada, pois já tem o tempo de começo
         mais cedo estabelecido. Assim, coloque-se a tarefa s na fila de
         espera:}
        se s.p = 0
           F.põe(s)
{Quando aqui se chega, uma de duas coisas aconteceu: ou todas as tarefas
foram processadas (o que é fácil de verificar contabilizando o número de
tarefas tiradas da fila de espera), e portando T_f contém o tempo de
finalização mais cedo do projecto e todas as tarefas têm os seus tempos de
começo e fim o mais cedo possível bem estabelecidos; ou ficaram algumas
tarefas por processar, o que só pode acontecer se o projecto estiver mal
especificado por conter dependências circulares.}

Aplicando o algoritmo acima ao diagrama de precedências dado como exemplo obtêm-se sucessivamente os valores indicados na tabela:

Traçado do algoritmo
passo	A	B	C	D	E	F	G	H	I	J	K	T_f	F
inicialização	d = 2 c = 0 f = ? n = 0 p = 0	d = 1 c = 0 f = ? n = 1 p = 1	d = 5 c = 0 f = ? n = 1 p = 1	d = 4 c = 0 f = ? n = 1 p = 1	d = 3 c = 0 f = ? n = 1 p = 1	d = 2 c = 0 f = ? n = 1 p = 1	d = 3 c = 0 f = ? n = 1 p = 1	d = 2 c = 0 f = ? n = 3 p = 3	d = 2 c = 0 f = ? n = 1 p = 1	d = 3 c = 0 f = ? n = 0 p = 0	d = 5 c = 0 f = ? n = 1 p = 1	0	AJ
A processada	d = 2 c = 0 f = 2 n = 0 p = 0	d = 1 c = 2 f = ? n = 1 p = 0	d = 5 c = 2 f = ? n = 1 p = 0	d = 4 c = 2 f = ? n = 1 p = 0	d = 3 c = 0 f = ? n = 1 p = 1	d = 2 c = 0 f = ? n = 1 p = 1	d = 3 c = 0 f = ? n = 1 p = 1	d = 2 c = 0 f = ? n = 3 p = 3	d = 2 c = 0 f = ? n = 1 p = 1	d = 3 c = 0 f = ? n = 0 p = 0	d = 5 c = 0 f = ? n = 1 p = 1	2	JBCD
J processada	d = 2 c = 0 f = 2 n = 0 p = 0	d = 1 c = 2 f = ? n = 1 p = 0	d = 5 c = 2 f = ? n = 1 p = 0	d = 4 c = 2 f = ? n = 1 p = 0	d = 3 c = 0 f = ? n = 1 p = 1	d = 2 c = 0 f = ? n = 1 p = 1	d = 3 c = 0 f = ? n = 1 p = 1	d = 2 c = 0 f = ? n = 3 p = 3	d = 2 c = 0 f = ? n = 1 p = 1	d = 3 c = 0 f = 3 n = 0 p = 0	d = 5 c = 3 f = ? n = 1 p = 0	3	BCDK
B processada	d = 2 c = 0 f = 2 n = 0 p = 0	d = 1 c = 2 f = 3 n = 1 p = 0	d = 5 c = 2 f = ? n = 1 p = 0	d = 4 c = 2 f = ? n = 1 p = 0	d = 3 c = 3 f = ? n = 1 p = 0	d = 2 c = 0 f = ? n = 1 p = 1	d = 3 c = 0 f = ? n = 1 p = 1	d = 2 c = 0 f = ? n = 3 p = 3	d = 2 c = 0 f = ? n = 1 p = 1	d = 3 c = 0 f = 3 n = 0 p = 0	d = 5 c = 3 f = ? n = 1 p = 0	3	CDKE
C processada	d = 2 c = 0 f = 2 n = 0 p = 0	d = 1 c = 2 f = 3 n = 1 p = 0	d = 5 c = 2 f = 7 n = 1 p = 0	d = 4 c = 2 f = ? n = 1 p = 0	d = 3 c = 3 f = ? n = 1 p = 0	d = 2 c = 7 f = ? n = 1 p = 0	d = 3 c = 0 f = ? n = 1 p = 1	d = 2 c = 0 f = ? n = 3 p = 3	d = 2 c = 0 f = ? n = 1 p = 1	d = 3 c = 0 f = 3 n = 0 p = 0	d = 5 c = 3 f = ? n = 1 p = 0	7	DKEF
D processada	d = 2 c = 0 f = 2 n = 0 p = 0	d = 1 c = 2 f = 3 n = 1 p = 0	d = 5 c = 2 f = 7 n = 1 p = 0	d = 4 c = 2 f = 6 n = 1 p = 0	d = 3 c = 3 f = ? n = 1 p = 0	d = 2 c = 7 f = ? n = 1 p = 0	d = 3 c = 6 f = ? n = 1 p = 0	d = 2 c = 0 f = ? n = 3 p = 3	d = 2 c = 0 f = ? n = 1 p = 1	d = 3 c = 0 f = 3 n = 0 p = 0	d = 5 c = 3 f = ? n = 1 p = 0	7	KEFG
K processada	d = 2 c = 0 f = 2 n = 0 p = 0	d = 1 c = 2 f = 3 n = 1 p = 0	d = 5 c = 2 f = 7 n = 1 p = 0	d = 4 c = 2 f = 6 n = 1 p = 0	d = 3 c = 3 f = ? n = 1 p = 0	d = 2 c = 7 f = ? n = 1 p = 0	d = 3 c = 6 f = ? n = 1 p = 0	d = 2 c = 0 f = ? n = 3 p = 3	d = 2 c = 0 f = ? n = 1 p = 1	d = 3 c = 0 f = 3 n = 0 p = 0	d = 5 c = 3 f = 8 n = 1 p = 0	8	EFG
E processada	d = 2 c = 0 f = 2 n = 0 p = 0	d = 1 c = 2 f = 3 n = 1 p = 0	d = 5 c = 2 f = 7 n = 1 p = 0	d = 4 c = 2 f = 6 n = 1 p = 0	d = 3 c = 3 f = 6 n = 1 p = 0	d = 2 c = 7 f = ? n = 1 p = 0	d = 3 c = 6 f = ? n = 1 p = 0	d = 2 c = 6 f = ? n = 3 p = 2	d = 2 c = 0 f = ? n = 1 p = 1	d = 3 c = 0 f = 3 n = 0 p = 0	d = 5 c = 3 f = 8 n = 1 p = 0	8	FG
F processada	d = 2 c = 0 f = 2 n = 0 p = 0	d = 1 c = 2 f = 3 n = 1 p = 0	d = 5 c = 2 f = 7 n = 1 p = 0	d = 4 c = 2 f = 6 n = 1 p = 0	d = 3 c = 3 f = 6 n = 1 p = 0	d = 2 c = 7 f = 9 n = 1 p = 0	d = 3 c = 6 f = ? n = 1 p = 0	d = 2 c = 9 f = ? n = 3 p = 1	d = 2 c = 0 f = ? n = 1 p = 1	d = 3 c = 0 f = 3 n = 0 p = 0	d = 5 c = 3 f = 8 n = 1 p = 0	9	G
G processada	d = 2 c = 0 f = 2 n = 0 p = 0	d = 1 c = 2 f = 3 n = 1 p = 0	d = 5 c = 2 f = 7 n = 1 p = 0	d = 4 c = 2 f = 6 n = 1 p = 0	d = 3 c = 3 f = 6 n = 1 p = 0	d = 2 c = 7 f = 9 n = 1 p = 0	d = 3 c = 6 f = 9 n = 1 p = 0	d = 2 c = 9 f = ? n = 3 p = 0	d = 2 c = 9 f = ? n = 1 p = 0	d = 3 c = 0 f = 3 n = 0 p = 0	d = 5 c = 3 f = 8 n = 1 p = 0	9	HI
H processada	d = 2 c = 0 f = 2 n = 0 p = 0	d = 1 c = 2 f = 3 n = 1 p = 0	d = 5 c = 2 f = 7 n = 1 p = 0	d = 4 c = 2 f = 6 n = 1 p = 0	d = 3 c = 3 f = 6 n = 1 p = 0	d = 2 c = 7 f = 9 n = 1 p = 0	d = 3 c = 6 f = 9 n = 1 p = 0	d = 2 c = 9 f = 11 n = 3 p = 0	d = 2 c = 9 f = ? n = 1 p = 0	d = 3 c = 0 f = 3 n = 0 p = 0	d = 5 c = 3 f = 8 n = 1 p = 0	11	I
I processada	d = 2 c = 0 f = 2 n = 0 p = 0	d = 1 c = 2 f = 3 n = 1 p = 0	d = 5 c = 2 f = 7 n = 1 p = 0	d = 4 c = 2 f = 6 n = 1 p = 0	d = 3 c = 3 f = 6 n = 1 p = 0	d = 2 c = 7 f = 9 n = 1 p = 0	d = 3 c = 6 f = 9 n = 1 p = 0	d = 2 c = 9 f = 11 n = 3 p = 0	d = 2 c = 9 f = 11 n = 1 p = 0	d = 3 c = 0 f = 3 n = 0 p = 0	d = 5 c = 3 f = 8 n = 1 p = 0	11

4.1.3 Diagrama de Gantt

Uma vez obtido o planeamento conducente ao tempo mínimo de execução do projecto, pode-se desenhar o seu diagrama de Gantt. Neste diagrama o tempo desenrola-se horizontalmente e cada tarefa é representada por uma barra:

Diagrama de Gantt
	0	1	2	3	4	5	6	7	8	9	10
A
B
C
D
E
F
G
H
I
J
K

4.1.4 Algoritmo inverso de planeamento

Observando os dois diagramas, o de precedências e o de Gantt, é fácil verificar que as tarefas I e J não precisam de ser realizadas logo no início do projecto: ambas têm uma folga de três unidades de tempo. Será possível quantificar as folgas para todas as tarefas? A resposta é sim, e isso consegue-se à custa dum algoritmo muito semelhante ao anterior, mas que é executado a partir do fim e para calcular os tempos de começo e fim de cada tarefa o mais tarde possível. Assim, sendo:

t.C - começo da tarefa t o mais tarde possível
t.F - fim da tarefa t o mais tarde possível

o algoritmo pode-se escrever:

{Para inicializar, atribua-se o valor T_f ao tempo de finalização o mais tarde possível t.F de cada tarefa t, atribua-se também o número t.m de sucessoras da tarefa t ao contador t.p e coloquem-se as tarefas sem sucessoras na fila F.}
{Enquanto a fila de tarefas a processar não estiver vazia:}
enquanto ~ F.vazia() faça-se:
    {Seja t a tarefa à frente da fila. Como as tarefa só são colocadas na fila
     quando as suas sucessoras directas já foram processadas, esta tarefa
     t já tem o valor correcto do tempo de finalização mais tarde
     possível t.F:}
    t <- F.frente()
    {Retire-se essa tarefa da fila:}
    F.tira()
    {Calcule-se o tempo de começo o mais tarde possível da tarefa:}
    t.C <- t.F - t.d
    {Agora que já se sabe qual o tempo de começo mais tarde de t,
     deve-se influenciar o tempo de finalização mais tarde das suas
     predecessoras directas:}
    para todas as tarefas p predecessoras directas de t faça-se:
        {Se o tempo de começo mais tarde de t é inferior ao tempo de
         finalização mais tarde de p (predecessora de t), então a
         finalização mais tarde de p tem de ser aumentada:}
        se t.C < p.F então
           p.F <- t.C
        {Diminua-se o contador de sucessoras já processadas de p,
         pois a tarefa t acabou de ser processada:}
        p.p <- p.p - 1
        {Se o número de sucessoras processadas chegou a zero, então p
         é candidata a ser processada, pois já tem o tempo de finalização
         mais tarde estabelecido. Assim, coloque-se a tarefa p na fila de
         espera:}
        se p.p = 0
           F.põe(p)
{Quando aqui se chega, uma de duas coisas aconteceu: ou todas as tarefas
foram processadas (o que é fácil de verificar contabilizando o número de
tarefas tiradas da fila de espera), e portando todas as tarefas têm os seus
tempos de começo e fim o mais tarde possível bem estabelecidos; ou ficaram
algumas tarefas por processar, o que só pode acontecer se o projecto
estiver mal especificado por conter dependências circulares.}

A diferença entre t.C e t.c (ou entre t.F e t.f) é a folga na colocação da tarefa t. Significa que a tarefa pode ter começo num intervalo de instantes de tempo de largura t.C - t.c. Essas folgas podem ser representadas no diagrama de Gantt (folgas a verde):

Diagrama de Gantt com folgas
	0	1	2	3	4	5	6	7	8	9	10
A
B
C
D
E
F
G
H
I
J
K

Todas as tarefas que têm folga nula são chamadas tarefas críticas: para reduzir o tempo total de execução do projecto é necessário encurtar pelo menos uma das tarefas críticas. As tarefas críticas são indicadas no diagrama com um sublinhado.

Finalmente, é de notar que se podem usar algoritmos muito semelhantes aos apresentados para fazer um plano do projecto respeitando tanto quanto possível tempos de começo e fim do projecto e tempos de começo das tarefas especificados pelo utilizador do programa, i.e., sem minimizar o tempo de conclusão do projecto. Pense no assunto.

Os algoritmos de planeamento serão abordados no Problema 3 da avaliação.

4.2 Sugestões

A tarefa de identificação das classes relevantes para uma dada aplicação é uma das mais importantes em programação orientada para objectos. No entanto, porque o enfoque desta disciplina não se restringe a esse assunto, apresenta-se uma lista de possíveis classes presentes na resolução do trabalho:

Tarefa - Esta classe representa a interface comum a todos os tipos de tarefas. Muito provavelmente deverá ser uma classe abstracta, pois qualquer instância concreta de tarefa terá de pertencer a uma das suas subclasses.
Projecto - Representa um projecto e possui mecanismos de planeamento e orçamentação. Deverá ser possível acrescentar tarefas a um projecto, acrescentar dependências, etc. Na realidade, para que se possa usar polimorfismo nas tarefas, deverá ser possível acrescentar ponteiros para tarefas. A implementação desta classe implicará a existência de um conjunto de nós de projecto (indexáveis pela sua etiqueta), ou seja, uma tabela ou mapa. Cada um desses nós é uma instância duma classe Nó, embutida na classe Projecto e privada, e possuirá pelo menos:

Um ponteiro para a tarefa respectiva.
Uma lista de ponteiros para os nós correspondentes a tarefas predecessoras.
Uma lista de ponteiros para os nós correspondentes a tarefas sucessoras.
Os tempos de começo e fim (mais cedo possível, mais tarde possível e efectivos) da tarefa de acordo com o planeamento.

Tabela - Classe modelo. Os nós do projecto (e, em cada nó, os ponteiros para os nós predecessores e sucessores), podem ser guardados em tabelas indexadas pela etiqueta. É mais fácil se implementar o conceito de tabela à priori (comece por uma implementação simples usando listas).

Em termos de escalonamento do trabalho, sugere-se que se comece por desenhar uma classe concreta Tarefa contendo apenas a respectiva duração (só para efeitos de teste), e que em seguida se desenhe, implemente e teste a classe Projecto, mas apenas no que diz respeito ao planeamento. Esta primeira fase corresponderá grosso modo ao Problema 3 da avaliação. Em seguida deve-se equipar a classe Tarefa de modo a proporcionar não só a duração, mas também os recursos humanos usados e os custos de material e mão de obra. Esta nova versão da classe permitirá testar a parte de orçamentação da classe Projecto. Finalmente, dever-se-á passar à implementação da classe Tarefa como origem abstracta de uma hierarquia de quatro subclasses representando os quatro tipos de tarefa sugeridos no enunciado. Note-se que, se os passos anteriores tiverem sido bem pensados, o facto da classe Tarefa ter passado a ser abstrata não obrigará a alterar a implementação da classe Projecto.

Não se esqueça de que é importante testar o código à medida que o desenvolve. Nunca deixe os testes para o fim. Pior ainda é só tentar compilar quando já escreveu o código todo. Para seu próprio bem, não o faça...

Algumas outras sugestões que poderá achar úteis para a escrita do programa:

Não é necessário fazer o planeamento sempre que há alguma alteração! Só é necessário fazê-lo antes de mostrar diagramas do projecto (e apenas se o planeamento anterior já não for válido). Ou quando o utilizador pedir para minimizar o tempo do projecto.
Construa uma meta-classe (ou classe modelo [template]) Projecto que seja parametrizável pelas tarefas (amanhã pode querer reutilizar a classe com outras tarefas muito diferentes). Siga esta sugestão apenas no final do desenvolvimento e só se tudo estiver a funcionar! Mesmo assim, faça uma cópia de segurança...
Para simplificar, admita que as etiquetas identificadoras das tarefas não podem possuir espaços em branco (nem tabuladores nem fins-de-linha).

4.3 Obrigatoriedades

Use como unidade temporal dias inteiros (pode admitir, se isso lhe for útil, que cada dia tem 8 horas de trabalho). Se quiser pode mostrar planeamento com datas absolutas ou com divisão em semanas (nestes casos considere semanas de trabalho com 5 dias úteis e ignore os feriados). O programa deve poder ser alterado com facilidade para trabalhar com planeamento horário, em vez de diário.
Use como unidade monetária escudos inteiros.
Use como unidade de área o m² inteiro e como unidade de comprimento o metro inteiro.
Não use as classes contentoras da biblioteca padrão do C++ (i.e., vector, list, queue, deque, map, multimap, set, multiset). Esta restrição deve-se unicamente a questões pedagógicas. Pretende-se que os alunos sejam capazes de desenvolver todas as ferramentas necessárias à implementação do trabalho. Seria muito interessante que os alunos também aprendessem a utilizar as principais classes da biblioteca padrão do C++, mas infelizmente não há tempo para isso. No entanto, as bases dadas nesta cadeira são suficientes para que os alunos compreendam facilmente os conceitos envolvidos nas classes definidas por essa biblioteca.

5 Avaliação

A avaliação do trabalho terá em conta, não só a correcta execução do programa, mas também, e principalmente, a correcta estruturação dos dados e métodos, funções e procedimentos que compõem o programa e ainda a sua legibilidade. Será dado muito valor à genericidade das soluções. I.e., se partes do programa puderem ser facilmente ser reutilizáveis noutros contextos (semelhantes ou não), melhor. Isso significa que a utilização de meta-classes (classe modelo), meta-funções (funções modelo), e classes desenhadas para poderem ser base duma hierarquia de classes sempre que justificável será valorizada.

A nota deste trabalho será dada apenas após uma discussão, individual, com cada um dos elementos do grupo. Nesta discussão qualquer elemento do grupo terá de demonstrar um total conhecimento do programa e ser capaz de operar as alterações que forem pedidas. Nessa oral poderão também ser feitas perguntas sobre a matéria em geral. A nota final dependerá não só da qualidade do trabalho, mas também, e principalmente, do conhecimento do mesmo programa e da matéria em geral e da capacidade de resolver problemas em C++ demonstrados nessa discussão.

Quaisquer funcionalidades extra que não tenham sido pedidas no enunciado, tais como menus sofisticados, interfaces com janelas, etc., não serão avaliadas.