Resumo da aula 11

Sumário

Programação genérica

1 Programação genérica

A abstracção é uma capacidade fundamental em programação. De acordo com Edsger W. Dijkstra

[...] the purpose of abstraction is not to be vague, but to create a new semantic level in which one can be absolutely precise.
Edsger W. Dijkstra, The Humble Programmer, Communications of the ACM, 15(10), October 1972.

ou seja

[...] o objectivo da abstracção não é que se possa ser vago, mas sim criar um novo nível semântico no qual se possa ser absolutamente preciso.

A genericidade pode ser vista como uma forma de introduzir um nível adicional de abstracção nos programas. O seu objectivo é permitir que um mesmo pedaço de código possa ser usado em contextos diferentes, evitando-se com isso a repetição. Escrever um pedaço de código genérico é perceber o que há de comum a uma família de algoritmos ou estruturas de dados, e abstrair aquilo que é comum daquilo que é variável.

Há várias formas de introduzir genericidade no código, como se verá. Em C++ essa genericidade introduz-se ao nível das rotinas e das classes e respectivas operações. À capacidade de uma rotina lidar com diferentes tipos de argumentos chama-se polimorfismo.

Em C++ há três tipos de polimorfismo:

Polimorfismo de sub-tipos ou dinâmico: é o polimorfismo das operações de uma classe base (super-tipo), muitas vezes abstracta, que podem ser invocadas a partir de um ponteiro ou referência para essa classe e que levam à execução do respectivo método especializado da classe derivada (sub-tipo) a que a instância apontada ou referenciada pertence. Neste tipo de polimorfismo são fundamentais os conceitos de derivação, rotina membro virtual e de ligação dinâmica. Normalmente utilizações da palavra "polimorfismo" sem mais qualificações referem-se a este tipo de polimorfismo.
Polimorfismo ad hoc ou estático: é o nome que também se dá à sobrecarga de nomes de rotinas, pois permite que a mesma sintaxe de invocação e o mesmo nome sejam usados com argumentos de diferentes tipos, sendo a versão apropriada das rotinas sobrecarregadas seleccionada automaticamente pelo compilador. Também se lhe pode chamar polimorfismo sintáctico.
Polimorfismo paramétrico: é o polimorfismo das operações que são parametrizadas por tipos, permitindo-lhes lidarem com diferentes tipos de argumentos. Está na base da programação genérica. É suportado em C++ pelos formulários ou templates, que tanto se aplicam a rotinas como a classes, como se verá.

Este resumo lida com a genericidade em C++, no entanto não arranha senão a superfície de um campo de enorme potencial e interesse, e que é assunto de intensa investigação e desenvolvimento neste momento.

1.1 Genericidade através da relação é um

As hierarquias de classes em C++ servem dois propósitos. O primeiro, e menos importante, é o de permitirem reaproveitamento de código através do mecanismo de herança. O segundo, e mais importante, é o de permitirem representar relações é um entre as classes da hierarquia.

Diz-se que uma classe base generaliza as correspondentes classes classes derivadas que, pelo contrário, a especializam. Assim, o suporte de relações é um pelo C++ introduz alguma genericidade na programação. Por exemplo, é possível implementar uma lista de ponteiros para a classe base A1 de uma hierarquia e guardar nela endereços de instâncias de qualquer classe derivada B1, C1, etc. Nesse sentido, pode-se dizer que a lista e respectivas operações são genéricas, pois tendo sido escritas em termos da classe base A1, podem ser usadas com instâncias de qualquer das classes suas derivadas: B1, C1, etc.

No entanto esta solução tem limitações. Se for necessária uma lista de ponteiros para a classe base A2 de uma outra hierarquia, sem relação com a primeira, não haverá outro remédio senão reproduzir todo o código relativo à lista original alterando o tipo dos seus itens para ponteiros para a nova classe base A2. O ideal seria que se pudesse escrever o código da lista de uma forma totalmente genérica, por forma a se poderem nela guardar instâncias de qualquer tipo.

A solução adoptada por linguagens que não possuem suporte para o polimorfismo paramétrico passa por um truque algo sujo. A ideia é que o polimorfismo de sub-tipos poderia ser usado para fornecer a genericidade pretendida se todas as classes fossem derivadas de uma única classe base! Linguagens como o Java adoptam esta solução. Nela todas as classes derivam directa ou indirectamente de uma classe base única que, por ter de generalizar todas as potenciais classes, recebe o nome de Object (melhor mereceria o nome de Coiso, pois um tal grau de generalização acaba por conduzir a uma classe sem nenhum significado...). Nessas linguagens há, no fundo, uma única hierarquia de classes. Assim, a definição de uma lista totalmente genérica é simples: basta que os seus itens sejam ponteiros para a classe Object.

O problema desta solução é que, através de um ponteiro para a classe Object, base da hierarquia unificada de todas as classes existentes, não é possível invocar operações que sejam fornecidas apenas pelas classes derivadas. Isso implica que os ponteiros para a classe Object sejam convertidos explicitamente em ponteiros para uma classe apropriada, que possua a operação desejada, por exemplo A1. Essa classe A1 será naturalmente derivada de Object (pois nessas linguagens todas as classes o são) e terá de ser base directa ou indirecta da classe a que pertence cada instância efectivamente apontada pelos itens da lista, por exemplo B1, C1, etc. O problema é que não há quaisquer garantias de que isso aconteça, pois é perfeitamente possível e legal colocar nessa lista endereços de instâncias de classes sem qualquer relação é um com a classe A1, por exemplo instâncias da classe A2 ou de classes B2, C2, etc. dela derivadas. O problema ocorre, portanto, por não existir qualquer relação entre as classe A1 e A2 mesmo sabendo que (a) qualquer instância de A1 é uma instância de Object e (b) qualquer instância de A2 é uma instância de Object. Assim, a conversão dos ponteiros contidos na lista do tipo (ponteiros para a classe Object) para ponteiros para a classe A1 não só pode falhar, por exemplo se a instância apontada for da classe A2, ou de classes suas derivada B2, C2, etc., como a ocorrência dessa falha de conversão só pode ser verificada durante a execução do programa, pois é apenas nessa altura que se pode saber a classe efectiva das instâncias apontadas.

O resultado da necessidade de conversões explícitas entre ponteiros para uma classe base e ponteiros para uma classe derivada é código que viola dois dos princípios mais importantes da programação: (a) quanto mais cedo ocorrerem os erros, melhor^* e (b) as opções do programador (e.g., guardar na lista objectos da classe A1 ou suas derivadas) devem ser explicitadas no código e no local mais óbvio (neste caso seria durante a definição da lista, e não durante a sua utilização). Além disso, a conversão entre ponteiros para uma classe base e ponteiros para uma classe derivada é uma operação morosa, pois é necessário verificar se a classe do objecto efectivamente apontado é compatível com a classe para a qual se pretende converter o ponteiro, o que leva a que esta solução além de perigosa, seja ineficiente.

Note-se que a solução original de definir dois tipos de lista, uma para a classe A1 e outra para a classe A2, apesar de desagradável pela repetição a que obriga, é perfeitamente segura, pois o compilador nunca permitiria inserir numa lista de ponteiros para A1 o endereço de uma instância de A2 ou de uma classe sua derivada, nem permitiria inserir numa lista de ponteiros para A2 o endereço de uma instância de A1 ou de uma classe sua derivada, não existindo relação é um entre essas duas classes.

A solução, como se verá, será introduzir o polimorfismo paramétrico, que permite definir apenas um tipo genérico de lista, parametrizável para qualquer tipo de item. Em particular esse tipo genérico de lista é parametrizável com as classe A1 e A2 referidas acima, sendo o resultado dessa parametrização duas classes de listas distintas de ponteiros para classes distintas, não relacionadas, o que permite ao compilador verificar erros de que só poderiam ser verificados em tempo de execução na solução da hierarquia única.

Adicionalmente, o polimorfismo paramétrico é ortogonal ao polimorfismo de sub-tipos, o que permite conjugar as vantagens de ambos os tipos de solução: polimorfismo paramétrico conducente a erros detectados durante a compilação e utilização de hierarquias de classes através do polimorfismo de sub-tipos sem necessidade de proceder a perigosas conversões entre ponteiros para classes base e ponteiros para classes derivadas.

^* É sempre preferível obter um erro de compilação a um erro de execução. Os erros de compilação não só são mais fáceis de corrigir, como não há o risco de ocorrerem pela primeira vez nas instalações do cliente, facto que teria efeitos desagradáveis para a reputação do programador e que poderia perfeitamente acontecer com a "solução" acima, por mais que o código tivesse sido testado.

1.2 Necessidade de genericidade

A genericidade introduzida pelo polimorfismo de sub-tipos, embora muito importante, não é suficiente.

1.2.1 Genericidade em rotinas

Suponha-se o problema de calcular o mínimo de dois valores. Se os valores forem do tipo int pode-se definir a função

/** Devolve o mínimo de a e b. @pre V. @post (mínimoDe = a a e a <= b) ou (mínimoDe = a b e b < a).*/ inline int mínimoDe(int const a, int const b) {
return a <= b ? a : b;
}

No entanto, é perfeitamente plausível que, no mesmo programa, seja necessário calcular o mínimo de pares de valores de outros tipos. Por exemplo, do tipo float. Para resolver o problema pode-se recorrer ao polimorfismo ad hoc, ou seja, à sobrecarga de nomes de rotinas, definindo uma nova função com o mesmo nome da anterior mas diferente tipo de parâmetros

/** Devolve o mínimo de a e b. @pre V. @post (mínimoDe = a a e a <= b) ou (mínimoDe = a b e b < a).*/ inline float mínimoDe(float const a, float const b) {
return a <= b ? a : b;
}

É fácil perceber onde conduz esta solução se for necessário calcular mínimos de pares de outros tipos de valores, por exemplo double e string

/** Devolve o mínimo de a e b.    @pre V.    @post (mínimoDe = a a e a <= b) ou (mínimoDe = a b e b < a).*/ inline double mínimoDe(double const a, double const b) {
    return a <= b ? a : b;
}

/** Devolve o mínimo de a e b.    @pre V.    @post (mínimoDe idêntico a a e a <= b) ou (mínimoDe idêntico a b e b < a).*/ inline string const& mínimoDe(string const& a, string const& b) {
   return a <= b ? a : b;
}

Da mesma forma que se sobrecarregou a função mínimoDe() para os tipos int, float, double e string, é possível sobrecarregá-la adicionalmente para uma classe definida pelo utilizador. Por exemplo, sendo a classe Moeda definida por

class Moeda {
public:
    Moeda(double const valor);
    double valor() const;

private:
    double valor_;
};

Moeda::Moeda(double const valor)
    : valor_(valor) {
}
double Moeda:: valor() const {     return valor_;
}
inline bool operator < (Moeda const& a, Moeda const& b) {
    retur a.valor() < b.valor();
}
// >, <=, >=, ==, !=

é possível fornecer a seguinte sobrecarga

/** Devolve o mínimo de a e b. @pre V. @post (mínimoDe idêntico a a e a <= b) ou (mínimoDe idêntico a b e b < a).*/ inline Moeda const& mínimoDe(Moeda const& a, Moeda const& b) {
return a <= b ? a : b;
}

Note-se que o corpo da função consiste numa instrução com exactamente o mesmo aspecto dos corpos das outras funções já definidas, o que acontece devido a se ter fornecido à classe Moeda o operador <=.

A observação do código acima permite concluir imediatamente que há repetição de código: para além das diferenças na forma de devolução e de passagem de argumentos (por valor vs. por referência), o código só varia no tipo dos parâmetros da função. Torna-se claro que se deveria tentar usar algum outro tipo de polimorfismo, que não o ad hoc, para definir a função mínimoDe() uma única vez e de uma forma genérica. O objectivo é ser claro, conciso, sintético e evitar erros, coisas que não acontecem com a solução usando sobrecarga. Como os tipos com os quais se pode querer usar a função genérica mínimoDe() não têm forçosamente qualquer relação entre si, a utilização de polimorfismo de sub-tipos, através do mecanismo da herança, está fora de questão. Sobra por isso o polimorfismo paramétrico.

1.2.2 Genericidade em classes

Suponha-se que é necessária a utilização de pilhas de inteiros num dado programa e que é aceitável que essas pilhas tenham uma capacidade máxima de 100 itens fixa em tempo de compilação. Pode-se definir uma classe PilhaFixaDeInt100 para representar o conceito em causa:

/** Representa pilhas com no máximo 100 itens to tipo int.   @invariant 0 <= número_de_itens <= N.*/ class PilhaFixaDeInt100 { public:     typedef int I;

    /** Constrói pilha vazia.       @pre V.       @post estaVazia().*/     PilhaFixaDeInt100();

    /** Devolve o item que está no topo da pilha.       @pre ¬estaVazia().       @post topo idêntico ao item no topo de *this.*/     I const& topo() const;

    /** Indica se a pilha está vazia.       @pre V.       @post estaVazia = *this está vazia.*/     bool estáVazia() const;

    /** Indica se a pilha está cheia.       @pre V.       @post estaCheia = *this está cheia.*/     bool estáCheia() const;

    /** Devolve altura da pilha.       @pre V.       @post altura = altura de *this.*/     int altura() const;

    /** Devolve o item que está no topo da pilha.       @pre ¬estaVazia().       @post topo idêntico ao item no topo de *this.*/     I& topo();

    /** Põe um novo item na pilha (no topo).       @pre V.       @post *this contém um item adicional no topo igual a novo_item.*/     void põe(I const& novo_item);

    /** Tira o item que está no topo da pilha.       @pre ¬estaVazia().       @post *this contém os itens originais menos o do topo.*/     void tiraItem(); private:     static int const N = 100;

    I itens[N];     int número_de_itens;

    /** Indica se a condição invariante de classe se verifica.       @pre V.       @post cumpreInvariante = (0 <= número_de_itens <= N).*/     bool cumpreInvariante() const; };

inline PilhaFixaDeInt100::PilhaFixaDeInt100()
    : número_de_itens(0) {     assert(cumpreInvariante());
}
inline PilhaFixaDeInt100::I const& PilhaFixaDeInt100::topo() const {
    assert(cumpreInvariante());
    assert(not estáVazia());
    return itens[número_de_itens - 1];
}
inline bool PilhaFixaDeInt100::estáVazia() const {
    assert(cumpreInvariante());
    return altura() == 0;
}
inline bool PilhaFixaDeInt100::estáCheia() const {
    assert(cumpreInvariante());
    return altura() == N;
}
inline int PilhaFixaDeInt100::altura() const {
    return número_de_itens;
}
inline PilhaFixaDeInt100::I& PilhaFixaDeInt100::topo() {
    assert(cumpreInvariante());
    assert(not estáVazia());
    return itens[número_de_itens - 1];
}
inline void PilhaFixaDeInt100::põe(I const& novo_ item) {
    assert(cumpreInvariante());
    assert(not estáCheia());
    itens[número_de_itens] = novo_ item;     ++número_de_itens;
    assert(cumpreInvariante());
}
inline void PilhaFixaDeInt100::tiraItem() {
    assert(cumpreInvariante());
    assert(not estáVazia());
    --número_de_itens;
    assert(cumpreInvariante());
}
inline bool PilhaFixaDeInt100::cumpreInvariante() const {
    return 0 <= numero_de_itens and numero_de_itens <= N;}

Este código tem um problema: é que se pode desejar que existam em simultâneo no programa pilhas de diferentes capacidades e com diferentes tipos de itens, e.g., double, string, Moeda, etc. Se isso acontecer, é necessário definir uma classe distinta para cada combinação da capacidade máxima com o tipo de itens armazenados, reproduzindo-se e adaptando-se para isso o código acima tantas vezes quantas for necessário, mudando o nome à classe apropriadamente.

É evidente que esta solução sofre exactamente dos mesmos problemas que a sobrecarga da função mínimoDe() na secção anterior: o código não é claro, muito menos conciso e sintético, não se evitam erros, torna-se a actualização da implementação da(s) classe(s) um pesadelo... Mais uma vez, há que usar polimorfismo para resolver este problema, sendo que:

o polimorfismo ad hoc não é solução, pois não se aplica a classes;
o polimorfismo de sub-tipos não é solução, pois os tipos dos itens a guardar não têm forçosamente qualquer relação entre si (e é duvidoso que devessem ter, como se viu na Secção 1.1.

1.3 Genericidade através de formulários (templates): rotinas e classes genéricas

A linguagem C++ suporta o polimorfismo paramétrico através dos chamados formulários (templates), que permitem definir rotinas e classes genéricas.

1.3.1 Rotinas genéricas

Voltando às várias funções para calcular o mínimo de dois valores de diferentes tipos, convém começar por identificar o que têm em comum. É claro que a comunalidade entre essas funções aumentaria se se optasse por uma única forma de devolução e passagem de argumentos. No caso dos tipos básicos do C++ não há qualquer vantagem em usar devolução ou passagem de argumentos por referência para constantes, mas também não há nenhuma desvantagem aparente. Por isso, pode-se aumentar o grau de comunalidade entre as funções se todas elas usarem esta forma de devolução e passagem de argumentos. Se isso for feito, é evidente que as funções variam apenas no tipo dos argumentos e da devolução. Chame-se T a esse tipo:

/** Devolve o mínimo de a e b. @pre V. @post (mínimoDe idêntico a a e a <= b) ou (mínimoDe idêntico a b e b < a).*/ inline T const& mínimoDe(T const& a, T const& b) {
return a <= b ? a : b;
}

Se se compilar esta função obtém-se naturalmente um erro de compilação: o compilador não sabe o que é T. É necessário deixar claro:

que se está a definir uma função genérica mínimoDe<>(), e não uma função normal; e
que o tipo T é um parâmetro desta função genérica, que deve ser substituído por um tipo para que se obtenha uma função normal.

1.3.1.1 Sintaxe

Para definir a função como genérica e T como um seu parâmetro usa-se a seguinte sintaxe:

/** Devolve o mínimo de a e b. @param T tipo dos argumentos. @pre V. @post (mínimoDe idêntico a a e a <= b) ou (mínimoDe idêntico a b e b < a).*/ template <typename T>
inline T const& mínimoDe(T const& a, T const& b) {
return a <= b ? a : b;
}

Tudo o que foi necessário foi preceder a definição da função da palavra-chave template, seguida de uma lista de parâmetros definidos entre parênteses agudos (<>). Neste caso existe apenas um parâmetro, que se indica explicitamente corresponder ao nome de um tipo usando a palavra-chave typename.

Em vez da palavra chame typename poder-se-ia ter usado a palavra-chave class, pois neste contexto são equivalentes. No entanto, é boa ideia discriminar entre as duas palavras chave para efeitos de melhor auto-documentação e legibilidade do programa:

Deve-se usar typename quando se puder usar qualquer tipo, mesmo que não seja uma classe.
Deve-se usar class quando apenas for admissível usar classes.

1.3.1.2 Instanciação

Uma vez definida uma função genérica, pode-se instanciá-la de modo a obter uma função lidando com um determinado tipo concreto. Para isso segue-se o nome da função genérica mínimoDe<>() de uma lista de argumentos colocados entre parênteses agudos. Deve ser passado um argumento compatível no lugar de cada parâmetro indicado na definição da função genérica. Neste caso há apenas um parâmetro que é o nome de um tipo, pelo que se pode usar como argumento qualquer dos tipos básicos do C++ ou qualquer outra classe (embora com restrições, como se verá):

cout << mínimoDe<int>(10, 5) << endl;
cout << mínimoDe<float>(1.3f, 4.4f) << endl;
cout << mínimoDe<double>(10.1, 5.5) << endl;
cout << mínimoDe<string>("olá", "mundo") << endl;
cout << mínimoDe<Moeda>(Moeda(1.0), Moeda(2.5)) << endl;

Repare-se que existem agora dois conjuntos de argumentos. Entre parêntese agudos (<>) os argumentos passados à função genérica para a instanciar. Entre parêntese curvos (()) os argumentos passados à função assim instanciada.

Em rigor, uma rotina genérica é instanciada apenas da primeira vez que é usada com determinados parâmetros. É apenas durante a instanciação da função genérica que o compilador verifica a validade do seu código. Este facto terá consequências importantes, como se verá.

1.3.1.3 Dedução automática dos argumentos

A linguagem C++ permite muitas vezes eliminar a instanciação explícita das rotinas genéricas, permitindo usar a sintaxe usual de invocação de rotinas para simultaneamente instanciar rotinas genéricas e invocar a rotina normal que resulta dessa instanciação. Para isso o compilador deduz sempre que possível os argumentos da rotina genérica a partir dos tipos dos argumentos passados entre parêntese curvos à função. Assim, é possível simplificar o código da secção anterior para:

cout << mínimoDe(10, 5) << endl;
cout << mínimoDe(1.3f, 4.4f) << endl;
cout << mínimoDe(10.1, 5.5) << endl;
cout << mínimoDe(Moeda(1.0), Moeda(2.5)) << endl;

Em alguns casos tal dedução não é possível, por exemplo:

cout << mínimoDe(10, 5.5) << endl;

Neste caso o que deveria o compilador fazer? Converter o valor literal 10 do tipo int para double e instanciar a função genérica com double ou converter o valor literal 5.5 do tipo double para int e instanciar a função genérica com int? Neste caso o compilador não pode adivinhar a intenção do programador, pelo que assinala um erro de compilação, dizendo que a invocação é ambígua. A solução neste caso está em fazer uma das conversões explicitamente

cout << mínimoDe(10, int(5.5)) << endl;
cout << mínimoDe(double(10), 5.5) << endl;

ou em passar argumentos à função genérica explicitamente

cout << mínimoDe<int>(10, 5.5) << endl;
cout << mínimoDe<double>(10, 5.5) << endl;

o que levará o compilador a fornecer a conversão apropriada para o argumento que dela necessita em cada caso.

Finalmente é de toda a conveniência falar de um caso patológico com resultado pouco intuitivo:

cout << mínimoDe("olá", "mundo") << endl;

Estranhamente o resultado neste caso tanto pode ser 'olá' como 'mundo'... A razão para isso tem a ver com o tipo das cadeias de caracteres literais, i.e., dos argumentos "olá" e "mundo" colocados na invocação da função genérica. Uma cadeia de caracteres literal é sempre do tipo

char const [n + 1]

onde n é o número de caracteres entre aspas. As cadeias de caracteres literais são, portanto, matrizes de caracteres com tantos elementos quantos os caracteres entre aspas adicionados de um elemento para conter o caractere '\0' usado para assinalar o fim das cadeias de caracteres clássicas do C++. No fundo tudo se passa como se estivessem definidas duas matrizes sem nome:

char const sem_nome₁[] = "olá"; char constsem_nome₂[] = "mundo";

cout << mínimoDe(sem_nome₁, sem_nome₂) << endl;

Mas, de acordo com a linguagem C++, quando numa expressão surge o nome de uma matriz, selvo em algumas ocasiões especiais como após o operador sizeof, esse nome é interpretado como um ponteiro para o primeiro elemento da matriz. Assim, o código acima é equivalente a:

char const sem_nome₁[] = "olá"; char constsem_nome₂[] = "mundo";

cout << mínimoDe(&sem_nome₁[0],&sem_nome₂[0]) << endl;

Ou seja, os dois argumentos são do tipo char const*, i.e., ponteiros para caracteres constantes. A função genérica mínimoDe<>() será, por isso, instanciada com T sendo char const*. Fica então claro porque são os resultados indefinidos: ao comparar a e b no corpo da função estão-se a comparar os endereços dos primeiros elementos das duas matrizes. Será seleccionado o endereço mais pequeno, qualquer que ele seja (note-se que em rigor a linguagem C++ só permite que sejam comparados através de operadores relacionais ponteiros para a elementos da mesma matriz).

A solução passa de novo ou pela conversão explícita para um tipo onde a comparação seja realizada da forma desejada (i.e., usando a ordenação lexicográfica), que neste caso é simplesmente a classe string, ou instanciando explicitamente a função genérica com esse mesmo tipo, o que leva à conversão implícita dos argumentos:

cout << mínimoDe(string("olá"), string("mundo")) << endl; cout << mínimoDe<string>("olá", "mundo") << endl;

1.3.1.4 Exemplo com dois argumentos e sem dedução automática

Uma rotina genérica pode ter mais do que um parâmetro. Suponha-se uma função que devolve um valor de vírgula flutuante convertido para um inteiro com arredondamento ^*.

/** Devolve o arredondamento de valor.    @pre V.    @post arredondamentoDe = inteiro mais próximo de valor e em caso
          de empate o mais longe de zero.*/ int arredondamentoDe(double const valor) {
    if(0 <= valor)
        return int(valor + 0.5);
    return int(valor - 0.5);
}

Também neste caso poderia existir a necessidade de arredondar valores de outros tipos de vírgula flutuante, e.g., float, para outros tipos de inteiros, e.g., long int. Mais uma vez se pode recorrer a uma função genérica, embora desta vez com dois parâmetros:

/** Devolve o arredondamento de valor.    @param F tipo de vírgula flutuante do argumento a converter com arredondamento.    @param I tipo inteiro do valor a devolver.    @pre V.    @post arredondamentoDe = inteiro mais próximo de valor e em caso
          de empate o mais longe de zero.*/ template <typename I, typename F>
I arredondamentoDe(F const valor) {
    if(0 <= valor)
        return I(valor + F(0.5));
    return I(valor - F(0.5));
}

Neste caso o C++ não consegue deduzir o tipo correspondente ao parâmetro I, uma vez que esse é o tipo do valor devolvido: a linguagem faz deduções apenas a partir dos argumentos. É, por isso, necessário passar argumentos explicitamente à função genérica:

cout << arredonda<long, double>(14.4) << endl;

Note-se que não se pode passar apenas um argumento (a não ser que os parâmetros restantes tenham argumentos por omissão), pois a linguagem não faz deduções parciais de parâmetros de rotinas genéricas.

^* A conversão de double para int, ou melhor, de qualquer valor de vírgula flutuante para qualquer inteiro limita-se a descartar a parte decimal do valor. Ou seja, trunca o valor, aproximando-o da origem. Fica como exercício para o leitor perceber porque se soma ou subtrai 0,5 ao valor a arredondar.

1.3.2 Classes genéricas

Viu-se nas secções anteriores que é possível condensar muito código recorrendo a rotinas genéricas. Nesta secção ver-se-á que no caso das classes a genericidade conduz a poupanças ainda maiores.

Em primeiro lugar é necessário identificar aquilo que se desejaria poder variar facilmente na classe PilhaFixaDeInt100. Neste caso é evidente que é o tipo dos itens na pilha e a sua capacidade máxima. Retirem-se as definições que fixam I e N em int e 100, respectivamente, e mudemos o nome da classe para algo mais genérico:

/** Representa pilhas com no máximo N itens do tipo intI.
   @invariant 0 <= número_de_itens <= N.*/ class PilhaFixaDeInt100 { public:     typedef int I;

    /** Constrói pilha vazia.       @pre V.       @post estaVazia().*/     PilhaFixaDeInt100();

    /** Devolve o item que está no topo da pilha.       @pre ¬estaVazia().       @post topo idêntico ao item no topo de *this.*/     I const& topo() const;

    /** Indica se a pilha está vazia.       @pre V.       @post estaVazia = *this está vazia.*/     bool estáVazia() const;

    /** Indica se a pilha está cheia.       @pre V.       @post estaCheia = *this está cheia.*/     bool estáCheia() const;

    /** Devolve altura da pilha.       @pre V.       @post altura = altura de *this.*/     int altura() const;

    /** Devolve o item que está no topo da pilha.       @pre ¬estaVazia().       @post topo idêntico ao item no topo de *this.*/     I& topo();

    /** Põe um novo item na pilha (no topo).       @pre V.       @post *this contém um item adicional no topo igual a novo_item.*/     void põe(I const& novo_item);

    /** Tira o item que está no topo da pilha.       @pre ¬estaVazia().       @post *this contém os itens originais menos o do topo.*/     void tiraItem(); private:     static int const N = 100;

    I itens[N];     int número_de_itens;

    /** Indica se a condição invariante de classe se verifica.       @pre V.       @post cumpreInvariante = (0 <= número_de_itens <= N).*/     bool cumpreInvariante() const; };

inline PilhaFixaDeInt100::PilhaFixaDeInt100()
    : número_de_itens(0) {     assert(cumpreInvariante());
}
inline PilhaFixaDeInt100::I const& PilhaFixaDeInt100::topo() const {
    assert(cumpreInvariante());
    assert(not estáVazia());
    return itens[número_de_itens - 1];
}
inline bool PilhaFixaDeInt100::estáVazia() const {
    assert(cumpreInvariante());
    return altura() == 0;
}
inline bool PilhaFixaDeInt100::estáCheia() const {
    assert(cumpreInvariante());
    return altura() == N;
}
inline int PilhaFixaDeInt100::altura() const {
    return número_de_itens;
}
inline PilhaFixaDeInt100::I& PilhaFixaDeInt100::topo() {
    assert(cumpreInvariante());
    assert(not estáVazia());
    return itens[número_de_itens - 1];
}
inline void PilhaFixaDeInt100::põe(I const& novo_item) {
    assert(cumpreInvariante());
    assert(not estáCheia());
    itens[número_de_itens] = novo_item;     ++número_de_itens;
    assert(cumpreInvariante());
}
inline void PilhaFixaDeInt100::tiraItem() {
    assert(cumpreInvariante());
    assert(not estáVazia());
    --número_de_itens;
    assert(cumpreInvariante());
}
inline bool PilhaFixaDeInt100::cumpreInvariante() const {
    return 0 <= numero_de_itens and numero_de_itens <= N;}

Se se tentar compilar o código tal como está ocorrerão erros de compilação, como seria de esperar, uma vez que o compilador não encontra definição para os nomes I e N.

1.3.2.1 Sintaxe

Para definir a classe como genérica e, I e N como seus parâmetros, usa-se a seguinte sintaxe:

/** Representa pilhas com no máximo N itens do tipo I.
    @param I tipo dos itens.   @param N número máximo de itens.   @invariant 0 <= número_de_itens <= N.*/ template <typename I, int const N>
class PilhaFixaDe { public:     /**Constrói pilha vazia.       @pre V.       @post estaVazia().*/     PilhaFixaDe();

    /** Devolve o item que está no topo da pilha.       @pre ¬estaVazia().       @post topo idêntico ao item no topo de *this.*/     I const& topo() const;

    /** Indica se a pilha está vazia.       @pre V.       @post estaVazia = *this está vazia.*/     bool estáVazia() const;

    /** Indica se a pilha está cheia.       @pre V.       @post estaCheia = *this está cheia.*/     bool estáCheia() const;

    /** Devolve altura da pilha.       @pre V.       @post altura = altura de *this.*/     int altura() const;

    /** Devolve o item que está no topo da pilha.       @pre ¬estaVazia().       @post topo idêntico ao item no topo de *this.*/     I& topo();

    /** Põe um novo item na pilha (no topo).       @pre V.       @post *this contém um item adicional no topo igual a novo_item.*/     void põe(I const& novo_item);

    /** Tira o item que está no topo da pilha.       @pre ¬estaVazia().       @post *this contém os itens originais menos o do topo.*/     void tiraItem(); private:     I itens[N];     int número_de_itens;

    /** Indica se a condição invariante de classe se verifica.       @pre V.       @post cumpreInvariante = (0 <= número_de_itens <= N).*/     bool cumpreInvariante() const; };

Mais uma vez, tudo o que foi necessário foi preceder a definição da função da palavra-chave template, seguida de uma lista de parâmetros definidos entre parênteses agudos (<>). Neste caso existem dois parâmetros. O primeiro é o nome de um tipo, facto indicado através da palavra chave typename. O segundo é uma constante inteira, pelo que se define da forma usual em C++.

Viu-se, pois, que os parâmetros de uma classe (ou rotina) genérica podem ser nomes de tipos ou inteiros. Na realidade também podem ser ponteiros para instâncias com ligação externa ou mesmo outras classes genéricas, embora esses casos estejam fora do âmbito desta disciplina.

1.3.2.2 Sintaxe da definição dos membros

A definição dos membros da classe fora da própria classe, neste caso apenas rotina membro, é um pouco mais trabalhosa. Isso deve-se ao facto de o compilador precisar de saber o que se está a definir são membros da classe genérica: é necessário precedê-los todas do mesmo prefixo e, além disso, acrescentar os parâmetros entre parênteses agudos após o nome da classe genérica (embora seja desnecessário fazê-lo após a ocorrência de PilhaFixaDe<I, N>:: como prefixo do nome do membro em definição. Tudo funciona como se os membros da classe também fossem genéricos (e de facto são-no):

template <typename I, int const N>
inline PilhaFixaDe<I, N>::PilhaFixaDe()
    : número_de_itens(0) {     ...}
template <typename I, int const N>
inline I const& PilhaFixaDe<I, N>::topo() const {
    ...}
template <typename I, int const N>
inline bool PilhaFixaDe<I, N>::estáVazia() const {
    ...}
template <typename I, int const N>
inline bool PilhaFixaDe<I, N>::estáCheia() const {
    ...}
template <typename I, int const N>
inline int PilhaFixaDe<I, N>::altura() const {
    ...}
template <typename I, int const N>
inline I& PilhaFixaDe<I, N>::topo() {
    ...}
template <typename I, int const N>
inline void PilhaFixaDe<I, N>::põe(I const& novo_item) {
    ...}
template <typename I, int const N>
inline void PilhaFixaDe<I, N>::tiraItem() {
    ...}
template <typename I, int const N>
inline bool PilhaFixaDe<I, N>::cumpreInvariante() const {
    ...}

1.3.2.3 Instanciação

As classes genéricas instanciam-se tal como as rotinas genéricas, embora não estejam sujeitas a dedução automática dos argumentos:

PilhaFixaDe<string, 10> ps;

ps.põe("Olá");
ps.põe("mundo!");

Note-se que também é possível definir classes embutidas genéricas e declarar operações genéricas e definir os respectivos métodos genéricos numa classe, quer ela seja ou não genérica. Suponha-se o seguinte pedaço de código:

PilhaFixaDe<int, 10> pi;

...

PilhaFixaDe<double, 10> pd(pi);

A última instrução gera um erro de compilação, pois, apesar de qualquer int poder ser convertido num double, o compilador não encontra nenhum construtor da classe PilhaFixaDe<double, 10> que receba uma instância da classe PilhaFixaDe<int, 10> como argumento. A solução para o problema passa por declarar e definir um construtor para a classe genérica que receba como argumento uma instância de uma qualquer instanciação da mesma classe genérica, desde que com a mesma capacidade máxima. Esse construtor terá, naturalmente, de ser ele próprio genérico, para poder lidar com qualquer tipo específico de pilha com a mesma capacidade máxima:

...

template <typename I, int const N>
class PilhaFixaDe { public:

    ...

    /** Constrói pilha por cópia da pilha original, que pode ser uma       pilha com a mesma capacidade, mas um tipo diferente de       itens, desde que atribuíveis aos da pilha a construir.        @pre V.       @post *this tem mesmo número de itens e itens com mesmo
              valor que itens de original, à parte alterações que
              possam ter ocorrido devido à conversão de tipo.*/     template <typename T>     PilhaFixaDe(PilhaFixaDe<T, N> const& original);

    ...

private:

    ...

    /* É necessário definir todas as instanciações da classe genérica      como amigas de qualquer instanciação. Só assim o construtor      por cópia generalizado funciona, pois acede ao atributo itens.*/     template <typename OutroI, int const OutroN>     friend class PilhaFixaDe;

    ...

};

...

template <typename I, int const N> template <typename T> PilhaFixaDe<I, N>::PilhaFixaDe(PilhaFixaDe<T, N> const& original)     : numero_de_itens(original.altura()) {    assert(original.cumpreInvariante());

    for(int i = 0; i != altura(); ++i)         itens[i] = original.itens[i];

    assert(cumpreInvariante());}

Veja-se a Secção 1.3.3 para saber o que acontece quando se tenta construir uma pilha à custa de outra cujos itens não são atribuíveis.

1.3.2.4 Parâmetros com argumentos por omissão

É possível especificar argumentos por omissão para os parâmetros de uma rotina ou classe genérica. Tal como no caso dos parâmetros com argumento por omissão para as rotinas normais, também no caso das classes e rotinas genéricas os parâmetros com argumentos por omissão devem ser especificados de tal forma que à direita de cada um deles não existam senão outros parâmetros também como argumentos por omissão. Dessa forma é possível omitir argumentos a partir da direita na lista de argumentos.

Suponha-se que, no caso da classe genérica PilhaFixaDe<typename I, int const N>, se pretendia que o parâmetro I tivesse int como argumento por omissão e o parâmetro N tivesse 100 como argumento por omissão. Nesse caso a definição da classe deveria ser modificada para:

...

template <typename I = int, int const N = 100>
class PilhaFixaDe {

...

};

...

Com tal definição (pouco útil na prática), seria possível escrever:

PilhaFixaDe<double, 1000> pd1;
PilhaFixaDe<double> pd2; // 100 itens double no máximo.
PilhaFixaDe<> pi; //100 itens int no máximo.

mas resultaria em erro escrever

PilhaFixaDe<> pi; // erro!

pois os parênteses agudos têm de estar sempre presentes.

1.3.2.4 Representação em UML

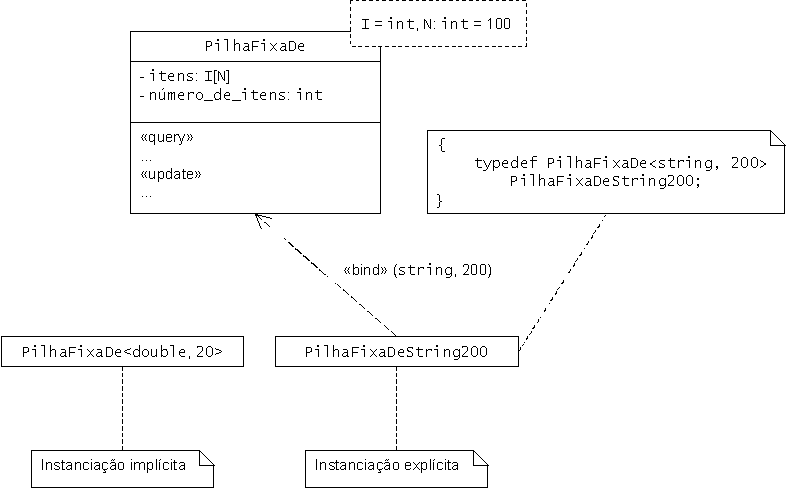
A representação em UML das classes genéricas é a que se apresenta abaixo. Notem-se os parâmetros da classe genérica colocados numa caixa a linha interrompida e incluindo argumentos por omissão:

1.3.3 Requisitos impostos aos argumentos

É apenas durante a instanciação da classe genérica que o compilador verifica a validade do código existente. Por outro lado, cada operação da classe é genérica por si só, pelo que a sua implementação (o método respectivo) só é compilada quando essa operação genérica é instanciada, o que acontece da primeira vez que o compilador encontra uma invocação dela. Assim, os requisitos quanto aos valores e tipos aceitáveis como argumentos de uma classe genérica estão implícitos no seu código. O melhor que se pode fazer é colocar um comentário indicando o que se espera dos argumentos na declaração da classe genérica. Por exemplo, no caso da classe genérica PilhaFixaDe<>, é obrigatório que o tipo I (tipo dos itens) tenha um construtor por omissão. Caso contrário seria impossível definir a matriz dos itens. Esse tipo também tem de suportar atribuições por cópia (veja-se a operação PilhaFixaDe<>::põe()). Por outro lado não é necessário que tenha construtor por cópia, pois os argumentos são sempre passados por referência e as devoluções também se fazem por referência. Finalmente, o parâmetro N tem de tomar sempre valores positivos, pois não se pode definir uma matriz clássica do C++ com 0 elementos, muito menos com um número de elementos negativo. Ou seja:

/** Representa pilhas com no máximo N itens do tipo I.
    @param I tipo dos itens, tem de ter construtor por omissão e
              atribuição por cópia.   @param N número máximo de itens, tem de ser positivo.   @invariant 0 <= número_de_itens <= N.*/ template <typename I, int const N>
class PilhaFixaDe {

    ...

};

...

De igual forma no caso da função genérica mínimoDe<>(), alterada aqui para usar o operador <, que é o o operador que se deve usar convencionalmente,

/** Devolve o mínimo de a e b. @param T tipo dos argumentos. @pre V. @post (mínimoDe idêntico a a e a <= b) ou (mínimoDe idêntico a b e b < a).*/ template <typename T>
inline T const& mínimoDe(T const& a, T const& b) {
return b < a ? b : a;
}

o código no corpo da função implica que um requisito do tipo T é que tenha o operador relacional < disponível. Esse facto deve ser deixado claro na documentação da função genérica:

/** Devolve o mínimo de a e b. @param T tipo dos argumentos, tem de ser comparável com o operador menor. @pre V. @post (mínimoDe idêntico a a e a <= b) ou (mínimoDe idêntico a b e b < a).*/ template <typename T>
inline T const& mínimoDe(T const& a, T const& b) {
return b < a ? b : a;
}

O mesmo se passa com o construtor por cópia genérico da classe genérica PilhaFixaDe<>. Passar-lhe como argumento, ainda que implicitamente, recorrendo à dedução automática de argumentos do C++, uma pilha cujos itens não sejam compatíveis com os itens da pilha em construção é um erro, mas apenas detectado durante a compilação da implementação do construtor, que ocorre aquando da sua instanciação. Por exemplo, dado o seguinte código:

PilhaFixaDe<int, 100> pi; PilhaFixaDe<Moeda, 100> pm(pi);

conduz a um erro de compilação com aspecto semelhante a:

pilha_fixa.C: In constructor `PilhaFixaDe<I, N>::PilhaFixaDe(const PilhaFixaDe<T, N>&) [with T = int, I = Moeda, int N = 100]': pilha_fixa.C:141: instantiated from here pilha_fixa.C:69: no match for `Moeda& = const int&' operator pilha_fixa.C:132: candidates are: Moeda& Moeda::operator=(const Moeda&)

Mais uma vez é desejável documentar os requisitos desse construtor modelo:

...

template <typename I, int const N>
class PilhaFixaDe { public:

    ...

    /** Constrói pilha por cópia da pilha original, que pode ser uma       pilha com a mesma capacidade, mas um tipo diferente de       itens, desde que atribuíveis aos da pilha a construir.
        @param T tipo dos itens da pilha original, tem de ser atribuível aos
               itens do tipo I.       @pre V.       @post *this tem mesmo número de itens e itens com mesmo
              valor que itens de original, à parte alterações que
              possam ter ocorrido devido à conversão de tipo.*/     template <typename T>     PilhaFixaDe(PilhaFixaDe<T, N> const& original);

    ...

};

...

É uma infelicidade da linguagem C++ que os requisitos acerca dos argumentos passados na instanciação de rotinas e classes genéricas não possa ser indicado explicitamente no código (salvo quanto ao facto de se tratar de um nome de um tipo, um inteiro, uma classe genérica, etc.). Este facto leva a erros de compilação difíceis de entender e a erros que ocorrem em locais pouco intuitivos (e sobretudo que deveriam ser desconhecidos do programador consumidor das rotinas e classes genéricas) e que ocorrem apenas, se e quando ocorrer a sua instanciação. Idealmente deveria haver uma forma de indicar na lista dos parâmetros os requisitos a verificar por cada argumento.

Apesar de não existir suporte na linguagem para a indicação explícita dos requisitos a cumprir pelos argumentos de uma rotina ou classe genérica, existem bibliotecas disponíveis que facilitam essa verificação. Essas bibliotecas, que estão fora do âmbito desta disciplina, fazem uso de aquilo a que a primeira biblioteca e mais importante biblioteca genérica em C++ (STL) chama conceitos e modelos [2]. Um conceito corresponde a um conjunto de requisitos que um tipo tem de verificar para se poder dizer um modelo desse conceito. Um conceito também pode ser visto como o conjunto de todos os possíveis tipos que verificam os seus requisitos. Por exemplo, existem os seguintes conceitos, entre outros:

Assignable: Um tipo T é modelo deste conceito se for possível copiar e atribuir instâncias desse tipo com a semântica habitual para essas operações. Note-se que, apesar do nome, não basta que as instâncias desse tipo sejam atribuíveis, têm de ser também construíveis por cópia.
Default Constructible: Um tipo T é modelo deste conceito se for possível construir por omissão instâncias desse tipo.
LessThen Comparable: Um tipo T é modelo deste conceito se for possível comparar instâncias desse tipo usando os operadores < ou >. Note-se que, apesar do nome, não basta que as instâncias desse tipo sejam comparáveis com o operador menor, têm de ser comparáveis também com o operador maior.

A documentação de rotinas e classes genéricas deve usar, tanto quanto possível, os conceitos existentes ou outros definidos para o efeito. Por exemplo:

/** Devolve o mínimo de a e b. @param T tipo dos argumentos, tem de ser modelo de LessThan Comparable. @pre V. @post (mínimoDe idêntico a a e a <= b) ou (mínimoDe idêntico a b e b < a).*/ template <typename T>
inline T const& mínimoDe(T const& a, T const& b) {
return b < a ? b : a;
}

/** Representa pilhas com no máximo N itens do tipo I.
    @param I tipo dos itens, tem de ser modelo de Assignable e de
            Default Contructible.   @param N número máximo de itens, tem de ser positivo.   @invariant 0 <= número_de_itens <= N.*/ template <typename I, int const N>
class PilhaFixaDe {

    ...

};

...

1.3.4 Implementação

Implementar bem uma classe ou rotina genérica não é fácil. Por isso é boa regra começar por desenhar, implementar e testar um ou mais casos particulares da rotina ou classe genérica. Só depois de testados se deve generalizar esses casos particulares. Depois de generalizado o código, deve-se voltar a testar, convertendo o teste de unidade original por forma a usar uma ou mais instanciações da classe ou rotina genérica a testar.

1.3.5 Especialização

É possível fornecer especializações de rotinas e classe genéricas para determinados argumentos. Isso pode ser útil quando a implementação precisar de ser diferente em alguns casos particulares. Por exemplo, se a classe Moeda não fosse um modelo de LessThan Comparable, ou seja, se os operadores < ou > não estivessem definidos, poder-se-ia fornecer uma especialização da rotina genérica capaz de lidar com o caso particular das moedas:

template <> inline Moeda const& minimoDe<Moeda>(Moeda const& a, Moeda const& b) { return b.valor() < a.valor() ? b : a; }

Da mesma forma é possível definir especializações de classes genéricas. Mas no caso das classes é também possível fazer especializações parciais, em que se mantém livre um dos parâmetros da classe genérica e se fixa o outro, ou em que se restringe o tipo de um ou mais parâmetros.

Suponha-se de novo a classe genérica PilhaFixaDe<>. Qualquer que seja o tipo dos itens especificado, é impossível especificar uma capacidade máxima de zero itens, pois a linguagem C++ não permite a definição de matrizes com zero elementos. Por exemplo,

PilhaFixaDe<double, 0> pd;

resulta num erro de compilação.

No entanto, por uma questão de coerência com a biblioteca padrão, em que se podem definir vectores de dimensão nula, seria interessante prever essa possibilidade. Isso consegue-se fornecendo uma especialização parcial da classe genérica para capacidades nulas:

/** Representa pilhas com no máximo 0 itens do tipo I.
    @param I tipo dos itens, tem de ser modelo de Assignable e de
            Default Contructible.   @invariant V.*/ template <typename I>
class PilhaFixaDe<I, 0> { public:

    ...

private:

private:    /** Indica se a condição invariante de classe se verifica.       @pre V.       @post cumpreInvariante = V.*/     bool cumpreInvariante() const; };
template <typename I> inline PilhaFixaDe<I, 0>::PilhaFixaDe() {     assert(cumpreInvariante()); }
template <typename I> template <typename T> PilhaFixaDe<I, 0>::PilhaFixaDe(PilhaFixaDe<T, 0> const& outra) {     assert(cumpreInvariante()); }
template <typename I> inline I const& PilhaFixaDe<I, 0>::topo() const {     assert(cumpreInvariante());     assert(not estaVazia());
    return I(); }
template <typename I> inline bool PilhaFixaDe<I, 0>::estaVazia() const {     assert(cumpreInvariante());
    return true; }
template <typename I> inline bool PilhaFixaDe<I, 0>::estaCheia() const {     assert(cumpreInvariante());
    return true; }
template <typename I> inline int PilhaFixaDe<I, 0>::altura() const {     return 0; }
template <typename I> inline I& PilhaFixaDe<I, 0>::topo() {     assert(cumpreInvariante());     assert(not estaVazia());
    return I(); }
template <typename I> inline void PilhaFixaDe<I, 0>::poe(I const& novo_item) {     assert(cumpreInvariante());     assert(not estaCheia());
    assert(cumpreInvariante()); }
template <typename I> inline void PilhaFixaDe<I, 0>::tiraItem() {     assert(cumpreInvariante());     assert(not estaVazia());
    assert(cumpreInvariante()); }
template <typename I> inline bool PilhaFixaDe<I, 0>::cumpreInvariante() const {     return true; }

Desta forma, quando a capacidade máxima especificada for zero, será instanciada a especialização da classe genérica. Caso contrário será instanciado o caso geral da classe genérica (sic). Assim, o código

PilhaFixaDe<double, 0> pd;

deixa de levar a um erro de compilação, como desejado.

1.3.6 Relação com a modularização física

Em termos de modularização física, é importante saber como se distribuem pelos vários ficheiros fonte as declarações e definições de rotinas e classe genéricas. As regras são as seguintes:

Classes genéricas definidas, como sempre, no ficheiro de interface .H.
Declarações de rotinas genéricas não-membro no ficheiro de interface .H.
Relativamente às rotinas genéricas, membro ou não, se a palavra-chave export estiver implementada:

Definições em-linha no ficheiro auxiliar de implementação _impl.H.
Definições não-em-linha no ficheiro de implementação .C com export.

Se export não estiver implementada:

Definições em-linha em _impl.H.
Definições não-em-linha também em _impl.H.

A palavra-chave export serve para se poderem definir rotinas genéricas no ficheiro de implementação. Isso só será possível quando a tecnologia de fusão aceitar pedaços de código por compilar, que serão compilados apenas durante a fase de fusão. Por enquanto tal não é possível em nenhum compilador/fusor conhecido para a linguagem C++.

2 Leitura recomendada

Recomenda-se a leitura do Capítulo 6 de [1].

3 Referências

[1] Michael Main e Walter Savitch, "Data Structures and Other Objects Using C++", Addison-Wesley, Reading Massachusetts, 1997.

[2] Matthew H. Austern, "Generic Programming and the STL: Using and Extending the C++ Standard Template Library", Addison-Wesley, Reading, Massachusetts, 1999.