Os alunos no final desta aula deverão conhecer:
Deverão também ser capazes de:
Caso os alunos sintam que os objectivos não foram atingidos na totalidade deverão concluir/repetir os exercícios desta aula autonomamente e ou recorrer aos horários de dúvidas.
Os ficheiros relativos a esta aula estão disponíveis no arquivo Aula3.zip.
ListaDeTelefonemas e ListaDeTelefonemas::Iterador
desenvolvidas
na Aula prática 2 e ilustradas na Figura
3.1.
A
implementação das operações
de inserção e remoção de um telefonema de ListaDeTelefonema são operações ineficientes, excepto
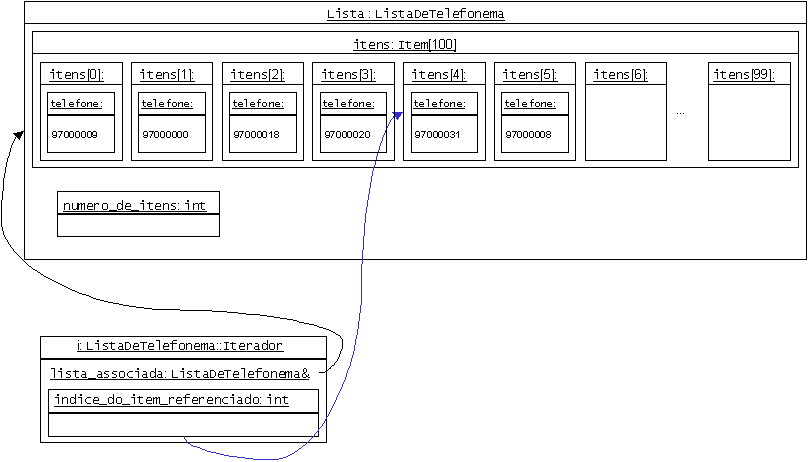
quando estas operações são realizadas no fim da lista.1.a) Identifique na Figura 3.1 os
valores em falta dos vários atributos das classes
ListaDeTelefonema e ListaDeTelefonema::Iterador usando a implementação
desenvolvida na Aula prática 2.

Figura 3.1
1. b) Como se remove um telefonema, referenciado por um iterador, da respectiva lista de telefonemas (use o cenário da Figura 3.1) ?
1.c) Que sucede ao iterador i, da Figura
3.1, depois de removido o item da
frente? E se a lista inicialmente só tiver um elemento?
2.a) Use a Figura 3.2 para identificar os
valores dos vários atributos das classes ListaDeTelefonema e ListaDeTelefonema::Iterador usando a implementação
representada na Aula teórica 3. Complete as ligações existentes entre os objectos da Figura
3.2.
2.b) Como se remove um telefonema, referenciado por um iterador, da respectiva lista de telefonemas (use o cenário da Figura 3.2)?
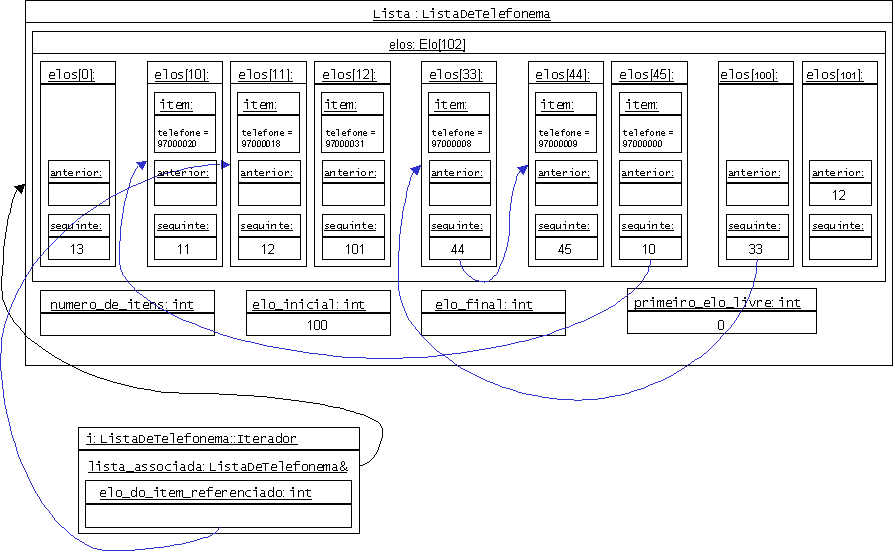
Figura 3.2
3. Considere a classe ListaDeTelefonema nos ficheiros lista_de_telefonema.H,
lista_de_telefonema_impl.H e lista_de_telefonema.C
(que pode encontrar na sua directoria ~/POO/Aula3).
3.a) Complete os seguintes métodos das classes ListaDeTelefonema
e ListaDeTelefonema::Iterador:
int ListaDeTelefonema::reservaElo();void ListaDeTelefonema::remove(Iterador& i); eIterador& ListaDeTelefonema::Iterador::operator++().3. b) Teste a nova lista com os programas de teste que se encontram em lista_de_telefonema.C.
e duracao_dos_telefonemas.C. Use o ficheiro de construção
fornecido (Makefile).
4. Refaça a ListaDeTelefonema para conter itens do tipo
double.
Pretende-se fazer um iterador que permita percorrer a lista de forma ordenada. Isto é, começa por se obter um iterador referenciando o item de menor valor que está na lista (ou o primeiro deles se houver mais que um igual). Depois, ao incrementar o iterador, deve-se obter o iterador para o item seguinte por ordem crescente dos seus valores. Para resolver este exercício siga os passos abaixo:
4.a) Faça uma classe
IteradorMenor que
permita percorrer todos os itens com o menor valor da lista.
A classe IteradorMenor
deve ser equipada com um construtor que construa um iterador para o primeiro
dos itens com o menor valor na lista recebida como argumento. Se a lista estiver vazia o
iterador deve-se referir ao item fictício final (depois do último).
A procura deste item é trivial, dados os algoritmos desenvolvidos
no primeiro semestre.
A incrementação de um IteradorMenor faz o seguinte:
vai desde o item referenciado pelo iterador antes da incrementação
até ao fim da lista à procura de um item com valor igual.
Se o encontrou, o novo valor do iterador deve-se referir a esse item. Caso
contrário, o iterador deve-se referir ao item fictício
final.
Faça um programa de teste que leia uma sequência de números para uma lista e escreva os menores no ecrã.
4.b) Transforme a classe IteradorMenor na classe
IteradorOrdenado.
A inicialização deste iterador faz-se como a do IteradorMenor.
O avanço também, excepto que, se não encontrar um
item de valor igual, deve colocar o iterador a referenciar o primeiro item
da lista com valor imediatamente acima. Se não existir, aí
sim, deve referenciar o elemento fictício final.
Faça um programa de teste que leia uma sequência de números para uma lista e os escreva de forma ordenada. O ciclo de escrita dos valores deve ser:
ListaDeDouble lista;...
//leitura de valores.
//Escrita ordenada:for(IteradorOrdenado i(l); i != l.fim(); ++i)cout << i.item() << endl;