Guião da 3ª Aula Teórica

Sumário

Guião

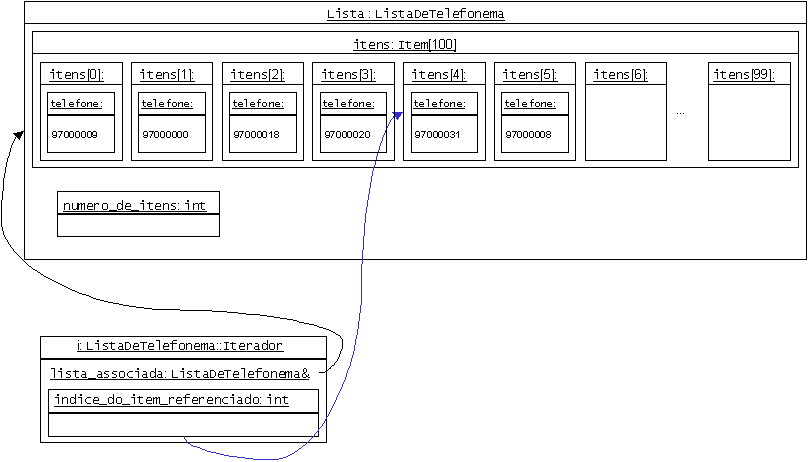
Começar por escrever as classes ListaDeInt e ListaDeInt::Iterador no quadro (versão simples com matrizes, da aula anterior).  Pelo menos as partes principais (e.g., eliminar documentação e asserções de CIC).  Explicá-las brevemente.

Basta pôr no quadro a definição das classes.  Explicar que se cortou a documentação apenas por razões de espaço!

class ListaDeInt {
  public:
    typedef int Item;
    class Iterador;
    ListaDeInt();
    Item const& frente() const;
    Item const& tras() const;
    int comprimento() const;
    bool estaVazia() const;
    bool estaCheia() const;
    Item& frente();
    Item& tras();
    void poeNaFrente(Item const& novo_item);
    void poeAtras(Item const& novo_item);

    void insereAntes(Iterador& iterador, Item const& novo_item);
    void tiraDaFrente();
    void tiraDeTras();
    void remove(Iterador& iterador);
    void esvazia();
    Iterador primeiro();
    Iterador ultimo();
    Iterador inicio();
    Iterador fim();

  private:

    static int const numero_maximo_de_itens = 100;

    Item itens[numero_maximo_de_itens];

    int numero_de_itens;

    bool cumpreInvariante() const;

    friend class Iterador;
};


class ListaDeInt::Iterador {
  public:
    explicit Iterador(ListaDeInt& lista_a_associar);
    Item& item() const;

    bool operator==(Iterador const& outro_iterador) const;
    bool operator!=(Iterador const& outro_iterador) const;
    Iterador& operator++();
    Iterador& operator--();
    Iterador operator++(int);
    Iterador operator--(int);
  private:
    ListaDeInt& lista_associada;
    int indice_do_item_referenciado;
    bool cumpreInvariante() const;
    friend class ListaDeInt;
};

Vamos ver uma pequena utilização de listas.  Suponham que se pretendia ler informação (nome e número) acerca de um conjunto de 100 alunos e depois escrevê-la por ordem alfabética do nome.  Podia-se começar por fazer uma classe para representar um aluno:

class Aluno {
  public:
    Aluno(string const& nome = "", int número = 0);
    string const& nome() const;
    int número() const;

  private:
    string nome_;
    int número_;
};

Aluno::Aluno(string const& nome = "", int número = 0)
    : nome_(nome), numero_(numero)
{
}

string const& Aluno::nome() const 
{
    return nome_;
}

int Aluno::número() const 
{
    return número_;
}

Agora, é só alterar a classe ListaDeInt para guardar alunos.  O que é preciso fazer?

Discutir alterações.  Concluir que é suficiente alterar o typedef e o nome da lista...

Falta agora o programa para ler os 100 alunos e escrevê-los por ordem alfabética.

int main()
{
    ListaDeAluno lista;

    for(int i = 0; i != 100; ++i) {
        string nome; // uma só palavra!
        int número;
        cin >> nome >> número;
        Aluno aluno(nome, número);

        // Inserir por ordem...
    }

    for(ListaDeAluno::Iterador i = lista.primeiro(); i != lista.fim(); ++i)
        cout << i.item().nome() << ' ' << i.item().numero() << endl;
}

Como inserir por ordem?

Discutir brevemente o algoritmo.  Concluir que tem de se procurar o primeiro nome maior ou igual e inserir antes.  Se não se encontrar, insere-se antes do fim.

int main()
{
    ListaDeAluno lista;

    for(int i = 0; i != 100; ++i) {
        string nome; // uma só palavra!
        int número;
        cin >> nome >> número;
        Aluno aluno(nome, número);

        ListaDeAluno::Iterador i = lista.primeiro();
        while(i != lista.fim and i.item().nome() < nome)
            ++i;

        lista.insereAntes(i, aluno);
    }

    for(ListaAluno::Iterador i = lista.primeiro(); i != lista.fim(); ++i)
        cout << i.item().nome() << ' ' << i.item().numero() << endl;
}

Perfeito!  Vimos que as listas, como estão, são muito simpáticas.  Mas...  Quando se insere sistematicamente a meio da lista (com acontece no programa que fizemos) a implementação que usámos para as lista é muito ineficiente.  Já viram o que acontece se um 100º aluno for uma Ana?  Fica a primeira da lista...  e isso implica empurrar todos os alunos que constam na lista para arranjar espaço na matriz dos itens...

E reparem que um problema semelhante ocorre quanto se removem itens que não estejam no fim da lista: é preciso puxar os que já lá estão para trás...  Ou melhor, para a frente!

Que se pode fazer para melhorar a situação?  Suponham que havia apenas três alunos na lista:

Ana
Carlos
Duarte

e que se pretende inserir o Berto antes do Carlos.  Porque é que temos de empurrar o Carlos e o Duarte?  Alguém sabe?

Discutir.  Solução: porque assumimos que a ordem dos itens na lista era a mesma que a ordem dos itens na matriz usada para os guardar...

Desenhar lista no quadro à semelhança das seguintes figuras da aula prática.  A ideia é ir fazendo a primeira figura evoluir para a segunda.

 

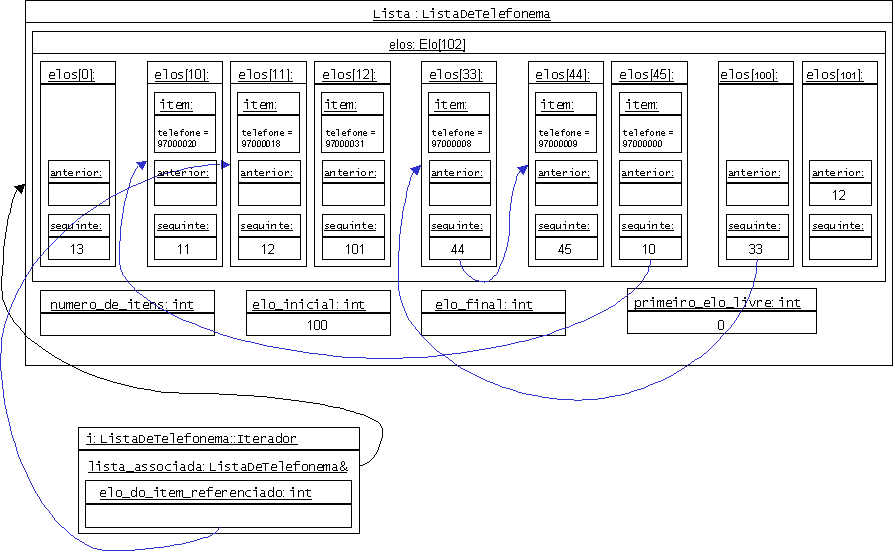
E se a ordem dos elementos na matriz pudesse ser diferente da ordem dos itens na lista?  Aí podia-se pôr o Berto no fim, sem deslocar ninguém...

Colocar.

Mas como saber então que o Berto está a seguir da Ana e antes do Carlos?

Discutir.  Concluir que cada elemento da matriz precisa de saber onde está item seguinte da lista.

Como representar essa informação?

Discutir possibilidades.  Concluir que se pode usar um índice em cada elemento da matriz!

Mas então, cada elemento da matriz guarda...  Um item e um índice...  Logo, já não basta uma matriz de itens...

Concluir que é necessária uma estrutura.  Chamar-lhe Elo (da cadeia).  Introduzir a noção de cadeia ligada.  Introduzir a noção de cadeia simplesmente ligada.

Construir a classe e usá-la na lista:

class ListaDeInt {
  public:

    ...

  private:
    struct Elo {
        Item item;
        int seguinte;
    };

    Elo elos[número_máximo_de_itens];

    ...
};

Representar as ligações por setas no quadro!

E agora?  Como definir o método ListaDeInt::insereAntes()?

inline void ListaDeInt::insereAntes(Iterador const& iterador,
                                    Item const& novo_item)
{
    assert(cumpreInvariante());
    assert(not estáCheia());
    assert(iterador != inicio());

    ++número_de_itens;

    ?

    assert(cumpreInvariante());
}

Discutir algoritmo.  Admitir que há uma operação privada reservaElo() que procura um elo livre na cadeia simplesmente ligada e que devolve o seu índice.  Concluir onde se guarda o item e que fazer ao índice do seguinte.

inline void ListaDeInt::insereAntes(Iterador const& iterador, 
                                    Item const& novo_item)
{
    assert(cumpreInvariante());
    assert(not estáCheia());
    assert(iterador != inicio());

    ++número_de_itens;

    int const elo_reservado = reservaElo();

    elos[elo_reservado].item = item;

    elos[elo_reservado].seguinte =
        iterador.elo_do_item_referenciado;

    ?

    assert(cumpreInvariante());
}

Tudo bem?  Não!  Porquê?  O elo anterior não está ligado ao que acabámos de inserir!  Temos de pôr o seu seguinte com o valor elo_reservado!  Mas onde está o elo anterior?

Discutir.  Concluir que não é forçosamente o elemento da matriz com o índice anterior.

Que fazer então?  Sugestões?

Discutir possibilidades.  Concluir que a mais simples é fazer a cadeia duplamente ligada.

Então é preciso alterar a classe Elo.  Alterar.

    struct Elo {
        Item item;
        int anterior;
        int seguinte;
    };

E agora o método ListaDeInt::insereAntes() fica...  Discutir calmamente...

inline void ListaDeInt::insereAntes(Iterador const& iterador,
                                    Item const& novo_item)
{
    assert(cumpreInvariante());
    assert(not estáCheia());
    assert(iterador != inicio());

    ++número_de_itens;

    int const elo_reservado = reservaElo();

    elos[elo_reservado].item = item;

    elos[elo_reservado].seguinte =
        iterador.elo_do_item_referenciado;

    int const anterior =
        elos[iterador.elo_do_item_referenciado].anterior;
    elos[anterior].seguinte = elo_reservado;

    ?

    assert(cumpreInvariante());
}

Falta alguma coisa?  Representar as ligações para trás no quadro...  Concluir que falta actualizar o índice do anterior na posição do iterador e do novo elo!

inline void ListaDeInt::insereAntes(Iterador const& iterador,
                                    Item const& novo_item)
{
    assert(cumpreInvariante());
    assert(not estáCheia());
    assert(iterador != inicio());

    ++número_de_itens;

    int const elo_reservado = reservaElo();

    elos[elo_reservado].item = item;

    elos[elo_reservado].anterior = 
         elos[iterador.elo_do_item_referenciado].anterior;
    elos[elo_reservado].seguinte =
        iterador.elo_do_item_referenciado;

    int const anterior =
        elos[iterador.elo_do_item_referenciado].anterior;
    elos[anterior].seguinte = elo_reservado;
    elos[iterador.elo_do_item_referenciado].anterior =
        elo_reservado;

    assert(cumpreInvariante());
}

Perfeito!  Perfeito?  Bolas... E se o iterador se referir ao item fictício antes da frente da lista?  É óbvio que a asserção falha...  Mas nesse caso, a que elo se refere o iterador?   Pior, como é que se sabe onde a cadeia de itens começa, i.e., onde está o primeiro item da lista?  Não é forçosamente o primeiro elemento da matriz!

Discutir assunto.  Dizer para se lembrarem dos itens fictícios da lista.

Os itens fictícios da lista têm um característica importante: "existem" (entre aspas) sempre, mesmo com a lista vazia.  Logo o problema resolve-se...

Discutir.  Concluir que dá jeito dar existência real aos itens fictícios!  Sugerir colocá-los no final da matriz, que passa a 102 elementos.

Discutir os elos que correspondem aos itens fictícios da cadeia: chamar-lhes guardas.  Logo, está-se a usar uma cadeia duplamente ligada com guardas.

Mas então o que deve fazer o construtor da lista?

Discutir.  Concluir que uma possibilidade é:

class ListaDeInt {

    ...

  private:

    ...

    static int const inicial = numero_máximo_de_itens;
    static int const final = numero_máximo_de_itens + 1;
};

ListaDeInt::ListaDeInt()
    : número_de_itens(0) 
{
    elos[inicial].seguinte = final;
    elos[final].anterior = inicial;

    ? // falta aqui qualquer coisa...

    assert(cumpreInvariante());
}

O anterior do inicial e o seguinte do final podem ficar com lixo...  Nunca são precisos!

E o método ListaDeInt::remove()?

Discutir.

Concluir:

inline void ListaDeInt::remove(Iterador& iterador)
{
    assert(cumpreInvariante());
    assert(iterador != inicio() and iterador != fim());

    --número_de_itens;

    int const elo_a_remover = iterador.elo_do_item_referenciado;

    // Avançar iterador!
    ++iterador;

    elos[elos[elo_a_remover].anterior].seguinte =
        elos[elo_a_remover].seguinte;
    elos[elos[elo_a_remover].seguinte].anterior =
        elos[elo_a_remover].anterior;

    libertaElo(elo_a_remover);

    assert(cumpreInvariante());
}

Discutir operação ListaDeInt::libertaElo().

Adiámos os problemas de reservar uma posição livre da matriz, quando se está a inserir um item, ou de libertar uma posição ocupada, quando se está a remover um item.

Discutir forma de saber que elementos da matriz estão livres.  Concluir que uma boa forma é usar um índice para primeiro livre e em cada elemento livre usar o índice para seguinte e fazer cadeia simplesmente ligada sem guardas de elos livres.  Notar que o construtor tem de ser alterado de modo a colocar todos os elementos da matriz (excepto as guardas) como elos livres.  Se necessário, deixar para as aulas práticas a discussão pormenorizada.

Discutir interface vs. implementação.   Concluir que se melhorou a classe sem alterar a sua interface.  Os programas que a usavam não precisam de ser alterados.

Deixar a implementação da parte restante da classe para as aulas práticas.