Guião da 11ª Aula Teórica

Sumário

  1. Genericidade.  O que é.
  2. Suportando genericidade com hierarquias de classes.  Objectos de classes derivadas podem ser tratados como se de objectos da classe base da hierarquia se tratassem.
  3. Exemplos em que a herança não é suficiente.
  4. Conceito de rotina genérica:
    1. Sintaxe.
    2. Utilização.
    3. Instanciação.
    4. Dedução automática de parâmetros.
  5. Conceito de classe genérica:
    1. Sintaxe.
    2. Rotinas membro (operações) também são genéricas.  Sintaxe.
    3. Utilização.
    4. Instanciação.
  6. Validação implícita dos parâmetros!  Necessidade de comentários!
  7. Parâmetros por omissão.  Utilização.
  8. Notação UML para classes genéricas, seus parâmetros, parâmetros por omissão, e instâncias.
  9. Construção de uma classe ou rotina genérica.  Identificação dos tipos e constantes que variam.  Passagem a parâmetros da rotina ou classe genérica.
  10. Regras para modularização física com classes e rotinas genéricas.

Guião

(Verificar se por acaso a palavra-chave export já está disponível!)

Escrever as funções, a pilha e a classe Moeda a priori no quadro, para poupar tempo.

Pode-se dizer que as hierarquias de classes em C++ servem dois propósitos.  O primeiro, e mais importante, é o de permitirem representar relações "é um" entre conceitos.  O segundo é o de permitirem reaproveitamento de código.

O suporte de relações "é um" pelo C++ introduz alguma genericidade na programação.  Por exemplo, no trabalho final torna-se possível tratar uniformemente qualquer Termo.  Onde se tiver um ponteiro para Termo e colocam-se lá ponteiros para vários tipos concretos de termos.  Depois tratam-se estes termos uniformemente.  Calcular o valor de um termo corresponde a invocar uma operação de cálculo declarada como abstracta na classe Termo mas para a qual todas as classes concretas fornecem um método apropriado, adequado ao seu tipo específico.

Esta genericidade, embora muito importante, não é suficiente.

Suponha-se o problema de calcular o mínimo de dois valores.  Se os valores forem int podemos escrever:

/** Devolve o mínimo de a e b.
    @pre V.
    @post (mínimoDe idêntico a a e a <= b) ou (mínimoDe idêntico a b e b < a). */
inline int mínimoDe(int const a, int const b)
{
    return a <= b ? a : b;
}

Mas, e se se quiser o mínimo de dois float?  Não há problema:

/** Devolve o mínimo de a e b.
    @pre V.
    @post (mínimoDe idêntico a a e a <= b) ou (mínimoDe idêntico a b e b < a). */
inline float mínimoDe(float const a, float const b)
{
    return a <= b ? a : b;
}

E se fossem double?  E string?  Tudo bem!

/** Devolve o mínimo de a e b.
    @pre V.
    @post (mínimoDe idêntico a a e a <= b) ou (mínimoDe idêntico a b e b < a). */
inline double mínimoDe(double const a, double const b)
{
    return a <= b ? a : b;
}

/** Devolve o mínimo de a e b.
    @pre V.
    @post (mínimoDe idêntico a a e a <= b) ou (mínimoDe idêntico a b e b < a). */
inline string const& mínimoDe(string const& a, string const& b)
{
   return a <= b ? a : b;
}

E se, depois de ter escrito todas as versões possíveis desta função (por sobrecarga do mesmo nome), eu criar uma classe Moeda?

class Moeda {
  public:
    Moeda(double const valor);
    double valor() const;

  private:
    double valor_;
};

Moeda::Moeda(double const valor)
    : valor_(valor)
{
}

double Moeda:: valor() const
{
    return valor_;
}

inline bool operator < (Moeda const& a, Moeda const& b)
{
    retur a.valor() < b.valor();
}

// >, <=, >=, ==, !=

Neste caso ainda preciso de:

/** Devolve o mínimo de a e b.
    @pre V.
    @post (mínimoDe idêntico a a e a <= b) ou (mínimoDe idêntico a b e b < a). */
inline Moeda const& mínimoDe(Moeda const& a, Moeda const& b)
{
   return a <= b ? a : b;
}

Há aqui algo de errado!  Esta funções são todas quase iguais, só variando praticamente no tipo dos parâmetros e do valor devolvido!

Se o nosso objectivo é ser claros, concisos, sintéticos, se o nosso objectivo é evitar erros, falta aqui qualquer coisa.

O que têm os erros a ver com isto?  É que, se detectássemos um erro no algoritmo usado nas funções teríamos de corrigir quantas versões?  Era provável que nos esquecêssemos de alguma...

E o pior é que os tipos com os quais podemos querer usar a função não têm forçosamente qualquer relação entre si...  Pelo que usar herança para resolver o problema está fora de questão...

[Se alguém perguntar:  Note-se que há linguagens que tentam resolver este problema dizendo que todos os tipos (mesmo os básicos) são classes que derivam de uma classe original chamada Objecto.  O problema com estas soluções é que introduzem relações entre classes que não têm qualquer utilidade.  Não é muito útil ter uma lista de ponteiros para Objecto se estes podem ser tão variados como inteiros ou formas ou alunos ou pontes ou alhos ou bugalhos...  Este tipo de solução implica tipicamente que o programador tenha de determinar explicitamente o tipo real dos objectos antes de com eles poder trabalhar.  Isso é inseguro.  É preferível restringir os tipos a priori, de modo que seja o compilador a avisar-nos de incompatibilidades.]

Mas há mais...  Nós de vez em quando voltamos à pilhas...  É uma classe recorrente nestas aulas.  Sim, outra vez!  Suponham uma solução em que o número máximo de itens na pilha é fixo a priori.  Chamo-lhe PilhaFixaDeInt100 por ser uma pilha de no máximo 100 inteiros:

/** Representa pilhas com no máximo 100 itens to tipo int.
    @invariant 0 <= número_de_itens <= N. */
class PilhaFixaDeInt100 {
  public:
    typedef int I;

    /** Constrói pilha vazia.
        @pre V.
        @post estaVazia(). */
    PilhaFixaDeInt100();

    /** Devolve o item que está no topo da pilha.
        @pre ¬estaVazia().
        @post topo idêntico ao item no topo de *this. */
    I const& topo() const;

    /** Indica se a pilha está vazia.
        @pre V.
        @post estaVazia = *this está vazia. */
    bool estáVazia() const;

    /** Indica se a pilha está cheia.
        @pre V.
        @post estaCheia = *this está cheia. */
    bool estáCheia() const;

    /** Devolve altura da pilha.
        @pre V.
        @post altura = altura de *this. */
    int altura() const;

    /** Devolve o item que está no topo da pilha.
        @pre ¬estaVazia().
        @post topo idêntico ao item no topo de *this. */
    I& topo();

    /** Põe um novo item na pilha (no topo).
        @pre V.
        @post *this contém um item adicional no topo igual a novo_item. */
    void põe(I const& novo_item);

    /** Tira o item que está no topo da pilha.
        @pre ¬estaVazia().
        @post *this contém os itens originais menos o do topo. */
    void tiraItem();
 
  private:
    static int const N = 100;

    I itens[N];
    int número_de_itens;

    bool cumpreInvariante() const;
};

inline PilhaFixaDeInt100::PilhaFixaDeInt100()
    : número_de_itens(0)
{
    assert(cumpreInvariante());
}

inline PilhaFixaDeInt100::I const& PilhaFixaDeInt100::topo() const
{
    assert(cumpreInvariante());
    assert(not estáVazia());

    return itens[número_de_itens - 1];
}

inline bool PilhaFixaDeInt100::estáVazia() const
{
    assert(cumpreInvariante());

    return altura() == 0;
}

inline bool PilhaFixaDeInt100::estáCheia() const
{
    assert(cumpreInvariante());

    return altura() == N;
}

inline int PilhaFixaDeInt100::altura() const
{
    return número_de_itens;
}

inline PilhaFixaDeInt100::I& PilhaFixaDeInt100::topo()
{
    assert(cumpreInvariante());
    assert(not estáVazia());

    return itens[número_de_itens - 1];
}

inline void PilhaFixaDeInt100::põe(I const& novo_ item)
{
    assert(cumpreInvariante());
    assert(not estáCheia());

    itens[número_de_itens] = novo_ item;
    ++número_de_itens;

    assert(cumpreInvariante());
}

inline void PilhaFixaDeInt100::tiraItem()
{
    assert(cumpreInvariante());
    assert(not estáVazia());

    --número_de_itens;

    assert(cumpreInvariante());
}

inline bool PilhaFixaDeInt100::cumpreInvariante() const
{
    return 0 <= numero_de_itens and numero_de_itens <= N;
}

Tudo isto é óptimo.  Mas temos aqui dois problemas.  O primeiro é que podemos estar interessados em pilhas de tamanho fixo mas com um diferente número máximo de itens.  O segundo é que podemos estar interessados numa pilha de double, por exemplo.  Ou numa pilha de string.  Ou numa pilha de Moeda...

Cada uma dessas classes se gera de uma forma simples: copia/cola seguido de alteração do número máximo de itens e do tipo dos itens, bem como do nome da classe...

É um enorme seca, como se deram conta com as utilizações da lista que fizeram no passado!

E além disso é uma prática que está sujeita a erros.  Se a minha implementação tiver um erro em quantos locais diferentes tenho de a alterar?

O C++ resolve estes problemas através das rotinas e classes genéricas ou templates (ou formulários).  Voltemos às funções para calcular o mínimo de dois valores.  O que têm em comum?  O que varia?

O que varia é apenas o tipo dos parâmetros e de devolução.  Chamemos T a esse tipo:

inline T const& mínimoDe(T const& a, T const& b)
{
    return a <= b ? a : b;
}

Notem que abusei um pouco...  Se se substituir T por Moeda ou string, obtém-se uma das funções originais.  Mas se substituir por int não...  Bom, mas se eu quero uniformizar, o melhor é passar tudo por referência constante, apesar se saber que no caso dos tipos básicos isso não acelera muito as coisas.  Não se pode ter tudo...

Notar também que a documentação apresentada não era correcta.  Só no caso da devolução por referência se pode falar em identidade.  Nos outros casos deveria ser igualdade...

Se mandarmos compilar esta função obtemos um erro de compilação.  Que diabos é T?  É preciso dizer ao C++ que isto não é uma função, é uma função genérica em que T é um parâmetro que deve ser substituído por um tipo.  A sintaxe é a seguinte:

/** Devolve o mínimo de a e b.
    @param T tipo dos argumentos.
    @pre V.
    @post (mínimoDe idêntico a a e a <= b) ou (mínimoDe idêntico a b e b < a). */
template <typename T>
inline T const& mínimoDe(T const& a, T const& b)
{
   return a <= b ? a : b;
}

Só isto!  E agora?  Bom, agora que temos uma função genérica podemos instanciá-la de modo a obter uma função para um tipo concreto.  Por exemplo:

cout << mínimoDe<int>(10, 5) << endl;
cout << mínimoDe<float>(1.3f, 4.4f) << endl;
cout << mínimoDe<double>(10.1, 5.5) << endl;
cout << mínimoDe<string>("olá", "mundo") << endl;
cout << mínimoDe<Moeda>(Moeda(1.0), Moeda(2.5)) << endl;

Repare-se que existem agora dois conjuntos de argumentos.  Entre <> os argumentos passados à função genérica.  Entre () os argumentos passados à função!

Em rigor, uma função genérica é instanciada apenas da primeira vez que é usada com determinados parâmetros!  E é apenas durante a instanciação da função genérica que o compilador verifica a validade do código.

Mas o melhor de tudo é que o C++ deduz sempre que possível os argumentos da função genérica a partir dos tipos dos argumentos da função!  Assim, é possível simplificar para:

cout << mínimoDe(10, 5) << endl;
cout << mínimoDe(1.3f, 4.4f) << endl;
cout << mínimoDe(10.1, 5.5) << endl;
cout << mínimoDe(Moeda(1.0), Moeda(2.5)) << endl;

A não ser, claro, em casos patológicos:

cout << mínimoDe(10, 5.5) << endl;

Neste caso o compilador deve converter o 10 para double e instanciar a função genérica com double ou converter o 5.5 para int e instanciar a função genérica com int?  O compilador não pode adivinhar, pelo que dá um erro de compilação!  A solução está em fazer uma das conversões explicitamente

cout << mínimoDe(10, int(5.5)) << endl;
cout << mínimoDe(double(10), 5.5) << endl;

ou em passar argumentos à função genérica explicitamente

cout << mínimoDe<int>(10, 5.5) << endl;
cout << mínimoDe<double>(10, 5.5) << endl;

E o caso:

cout << mínimoDe("olá", "mundo") << endl;

?  Está certo?

Explicar que não, porque os argumentos são do tipo char const*!

Claro está que uma rotina genérica pode ter mais do que um parâmetro.  Suponham uma função para converter um valor de vírgula flutuante para um inteiro com arredondamento.

Discutir solução.  Desenhar função no quadro para positivos e negativos.  Concluir:

/** Devolve o arredondamento de valor.
    @pre V.
    @post arredondamentoDe = inteiro mais próximo de valor e em caso 
          de empate o mais longe de zero. */
int arredondamentoDe(double const valor)
{
    if(0 <= valor)
        return int(valor + 0.5);
    return int(valor - 0.5);
}

Mas podíamos querer converter um float para long int, por exemplo.  Temos então uma função genérica com dois parâmetros:

/** Devolve o arredondamento de valor.
    @pre V.
    @post arredondamentoDe = inteiro mais próximo de valor e em caso 
          de empate o mais longe de zero. */
template <typename I, typename F>
I arredondamentoDe(F const valor) 
{
    if(0 <= valor)
        return I(valor + F(0.5));
    return I(valor - F(0.5));
}

Como utilizar?  Neste caso o C++ não consegue deduzir o tipo I porque esse é o tipo do valor devolvido!  É preciso passar argumentos explicitamente à rotina genérica:

cout << arredonda<long, double>(14.4) << endl;

Nota:  Não se pode passar apenas um argumento, a não ser que os parâmetros restantes tenham argumentos por omissão.

Óptimo! Vimos como poupar um montão de trabalho no caso das funções.

Passemos às classes.  Que gostaríamos poder variar facilmente na classe PilhaFixaDeInt100??  O tipo dos itens e o número máximo de itens!  Retiremos as definições que fixam I e N em int e 100 respectivamente e mudemos o nome da classe:

/** Representa pilhas com no máximo N itens do tipo intI.
    @invariant 0 <= número_de_itens <= N. */
class PilhaFixaDeInt100 {
  public:
    typedef int I;

    /** Constrói pilha vazia.
        @pre V.
        @post estaVazia(). */
    PilhaFixaDeInt100();

    /** Devolve o item que está no topo da pilha.
        @pre ¬estaVazia().
        @post topo idêntico ao item no topo de *this. */
    I const& topo() const;

    /** Indica se a pilha está vazia.
        @pre V.
        @post estaVazia = *this está vazia. */
    bool estáVazia() const;

    /** Indica se a pilha está cheia.
        @pre V.
        @post estaCheia = *this está cheia. */
    bool estáCheia() const;

    /** Devolve altura da pilha.
        @pre V.
        @post altura = altura de *this. */
    int altura() const;

    /** Devolve o item que está no topo da pilha.
        @pre ¬estaVazia().
        @post topo idêntico ao item no topo de *this. */
    I& topo();

    /** Põe um novo item na pilha (no topo).
        @pre V.
        @post *this contém um item adicional no topo igual a novo_item. */
    void põe(I const& novo_item);

    /** Tira o item que está no topo da pilha.
        @pre ¬estaVazia().
        @post *this contém os itens originais menos o do topo. */
    void tiraItem();
 
  private:
    static int const N = 100;

    I itens[N];
    int número_de_itens;

    bool cumpreInvariante() const;
};

inline PilhaFixaDeInt100::PilhaFixaDeInt100()
    : número_de_itens(0)
{
    assert(cumpreInvariante());
}

inline PilhaFixaDeInt100::I const& PilhaFixaDeInt100::topo() const
{
    assert(cumpreInvariante());
    assert(not estáVazia());

    return itens[número_de_itens - 1];
}

inline bool PilhaFixaDeInt100::estáVazia() const
{
    assert(cumpreInvariante());

    return altura() == 0;
}

inline bool PilhaFixaDeInt100::estáCheia() const
{
    assert(cumpreInvariante());

    return altura() == N;
}

inline int PilhaFixaDeInt100::altura() const
{
    return número_de_itens;
}

inline PilhaFixaDeInt100::I& PilhaFixaDeInt100::topo()
{
    assert(cumpreInvariante());
    assert(not estáVazia());

    return itens[número_de_itens - 1];
}

inline void PilhaFixaDeInt100::põe(I const& novo_item)
{
    assert(cumpreInvariante());
    assert(not estáCheia());

    itens[número_de_itens] = novo_item;
    ++número_de_itens;

    assert(cumpreInvariante());
}

inline void PilhaFixaDeInt100::tiraItem()
{
    assert(cumpreInvariante());
    assert(not estáVazia());

    --número_de_itens;

    assert(cumpreInvariante());
}

inline bool PilhaFixaDeInt100::cumpreInvariante() const
{
    return 0 <= numero_de_itens and numero_de_itens <= N;
}

Claro está que o compilador dá um montão de erros!  É necessário dizer-lhe que é uma classe genérica e que I e N são os respectivos!

/** Representa pilhas com no máximo N itens do tipo I.
    @param I tipo dos itens.
    @param N número máximo de itens.
    @invariant 0 <= número_de_itens <= N. */
template <typename I, int const N>
class PilhaFixaDe {
  public:

    /** Constrói pilha vazia.
        @pre V.
        @post estaVazia(). */
    PilhaFixaDe();

    /** Devolve o item que está no topo da pilha.
        @pre ¬estaVazia().
        @post topo idêntico ao item no topo de *this. */
    I const& topo() const;

    /** Indica se a pilha está vazia.
        @pre V.
        @post estaVazia = *this está vazia. */
    bool estáVazia() const;

    /** Indica se a pilha está cheia.
        @pre V.
        @post estaCheia = *this está cheia. */
    bool estáCheia() const;

    /** Devolve altura da pilha.
        @pre V.
        @post altura = altura de *this. */
    int altura() const;

    /** Devolve o item que está no topo da pilha.
        @pre ¬estaVazia().
        @post topo idêntico ao item no topo de *this. */
    I& topo();

    /** Põe um novo item na pilha (no topo).
        @pre V.
        @post *this contém um item adicional no topo igual a novo_item. */
    void põe(I const& novo_item);

    /** Tira o item que está no topo da pilha.
        @pre ¬estaVazia().
        @post *this contém os itens originais menos o do topo. */
    void tiraItem();
 
  private:
    I itens[N];
    int número_de_itens;

    bool cumpreInvariante() const;
};

O.k.!  Mas, e os membros da classe?  Como se definem?  O C++ tem de saber que são membros da classe genérica, pelo que, seca das secas, é necessário precedê-los todas do mesmo prefixo...  É como se os membros também fossem genéricos, e de facto são-no!

template <typename I, int const N>
inline PilhaFixaDe<I, N>::PilhaFixaDe()
    : número_de_itens(0)
{
    assert(cumpreInvariante());
}

template <typename I, int const N>
inline I const& PilhaFixaDe<I, N>::topo() const
{
    assert(cumpreInvariante());
    assert(not estáVazia());

    return itens[número_de_itens - 1];
}

template <typename I, int const N>
inline bool PilhaFixaDe<I, N>::estáVazia() const
{
    assert(cumpreInvariante());

    return altura() == 0;
}

template <typename I, int const N>
inline bool PilhaFixaDe<I, N>::estáCheia() const
{
    assert(cumpreInvariante());

    return altura() == N;
}

template <typename I, int const N>
inline int PilhaFixaDe<I, N>::altura() const
{
    return número_de_itens;
}

template <typename I, int const N>
inline I& PilhaFixaDe<I, N>::topo()
{
    assert(cumpreInvariante());
    assert(not estáVazia());

    return itens[número_de_itens - 1];
}

template <typename I, int const N>
inline void PilhaFixaDe<I, N>::põe(I const& novo_item)
{
    assert(cumpreInvariante());
    assert(not estáCheia());

    itens[número_de_itens] = novo_item;
    ++número_de_itens;

    assert(cumpreInvariante());
}

template <typename I, int const N>
inline void PilhaFixaDe<I, N>::tiraItem()
{
    assert(cumpreInvariante());
    assert(not estáVazia());

    --número_de_itens;

    assert(cumpreInvariante());
}

template <typename I, int const N>
inline bool PilhaFixaDe<I, N>::cumpreInvariante() const
{
    return 0 <= numero_de_itens and numero_de_itens <= N;
}

Como se instancia uma classe genérica?  Como para as funções, embora agora não haja dedução automática dos parâmetros:

PilhaFixaDe<string, 10> ps;

ps.põe("Olá");
ps.põe("mundo!");

Mais uma vez, é apenas durante a instanciação da classe genérica que o compilador verifica a validade do código.  Ou seja, os argumentos aceitáveis como argumentos da classe genérica estão implícitos no seu código!  O melhor que se pode fazer é colocar um comentário indicando o que se espera desse tipo na declaração da classe genérica.  Por exemplo, no caso da classe genérica PilhaFixaDe, é obrigatório que o tipo I (tipo dos itens) tenha um construtor por omissão.  Caso contrário será impossível definir a matriz dos itens!  Também tem de suportar atribuições por cópia (ver põe()).  Por outro lado não é necessário que tenha construtor por cópia, pois os argumentos são sempre passados por referência e as devoluções também se fazem por referência.  Finalmente o parâmetro N tem de tomar sempre valores positivos, pois não se pode definir uma matriz clássica do C++ com 0 elementos, muito menos com um número de elementos negativo.  Ou seja:

/** Representa pilhas com no máximo N itens do tipo I.
    @param I tipo dos itens, tem de ter construtor por omissão e 
              atribuição por cópia.
    @param N número máximo de itens, tem de ser positivo.
    @invariant 0 <= número_de_itens <= N. */
template <typename I, int const N>
class PilhaFixaDe {
  public:
    ...

[Isto convinha ser expandido nas teóricas!  Referir restrições a I e a N.]

Note-se que cada operação da classe é genérica por si só!  A sua implementação (o método respectivo) só é compilada quando essa operação genérica é instanciada, o que acontece da primeira vez que o compilador encontra uma invocação dessa operação.

Onde se colocam as rotinas e classes genéricas?

Regras:

Desenhar diagrama UML da pilha!

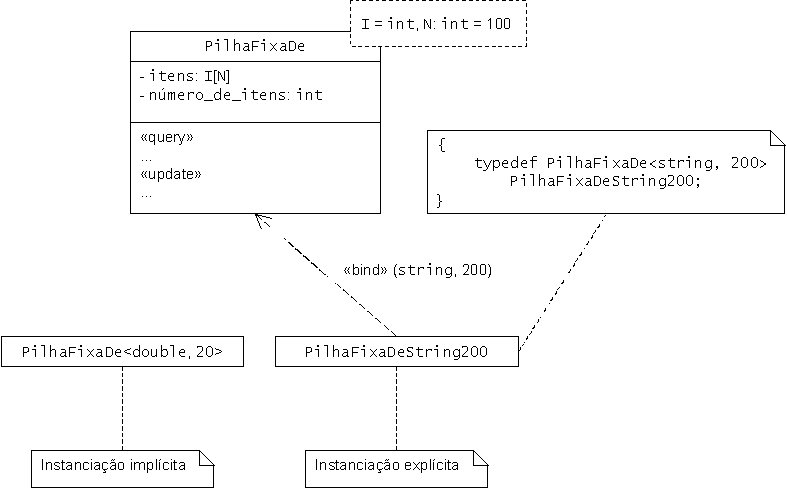
Discutir parâmetros por omissão: pilhas de 100 int.  É necessário usar <> na mesma!  Ensinar notação UML para parâmetros por omissão.

Desenhar bem uma classe ou rotina genérica não é fácil.  Por isso é boa regra começar por desenhar, implementar e testar um ou mais casos particulares da rotina ou classe genérica.  Só depois de testados se deve generalizar esses casos particulares.  E em seguida deve-se testar de novo!

Mencionar en passant especialização e especialização parcial.