you are here:
Main Menu
| Efficient methods for solving SDEs |
|
Mathematical modeling of random phenomena in Physics and Engineering:
analysis and efficient numerical simulations Background Analyzing random phenomena, for instance the
effect of random perturbations on deterministic dynamical systems, is of
paramount importance in a variety of problems, being rather ubiquitous.
Within such difficult problems, an explicit analytical solution can be
hardly found, thus pushing to the search for asymptotic or numerical
methods. Effective numerical methods for integrating stochastic
dynamical systems (that is systems of stochastic differential equations,
SDEs) are based, as a rule, on the generation of suitable sequences of
random numbers, which are often called ‘‘pseudorandom’’, to stress that
ideal randomness cannot be reproduced on real computers, but it is
highly inefficient.
 Scatter random points on the plane generated with pseudorandom and quasi-random number . Note that the quasi-random numbers are spread more uniformly over the plane 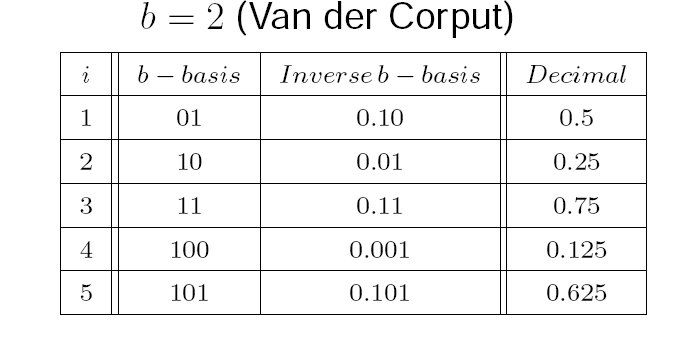
On the right, a sequence of quasi-random numbers of the Van der Corput-type.
Pick an integer, convert into binary, inverse, and convert back into decimal. An efficient method for solving SDEs
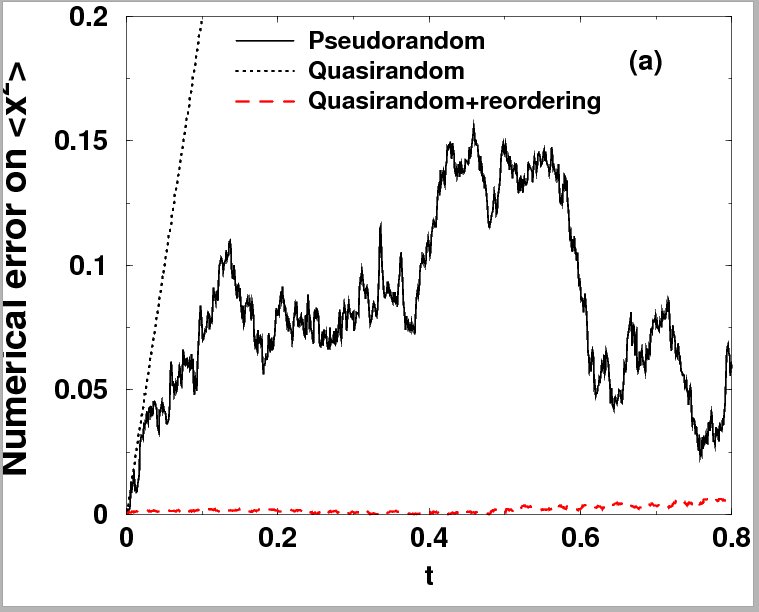
Numerical error made in computing the second moment of a 1D brownian motion versus time, using pseudorandom sequences of numbers, quasi-random, and quasi-random with reordering. Selected publications
|

 POSTDOC position NOW OPEN!
POSTDOC position NOW OPEN!