Main Menu
| Monte Carlo methods for matrix functions |
|
Efficient Monte Carlo methods for computing functions of matrices
Historically, the idea of using probabilistic methods based on Monte Carlo simulations for solving linear al
gebra problems goes back to the pioneering work of von Neumann and Ulam during the
1940's. Although initially the method was proposed merely for computing the inverse of a matrix, it was later generalized for solving linear algebra problems in a series
of seminal papers. Briefly the underlying idea consists in generating a discrete Markov chain
which evolves by random paths through the different indices of the matrix. Mathematically, the method can be
seen in a way as a Monte Carlo sampling of the Neumann series of the matrix.
Another related area of application of the probabilistic methods where some significant progress has recently made is in the field of matrix functions. In fact, in the specific case
of the action of a matrix exponential over a vector, we proposed recently a probabilistic method based on a multilevel Monte Carlo method, which as an important feature improves notably the typical slow convergence rate of any Monte Carlo method.
The method is based on generating random paths, which evolve through the indices of the matrix, governed now by a suitable continuous-time Markov chain. The vector solution is computed probabilistically by averaging over a suitable multiplicative functional.
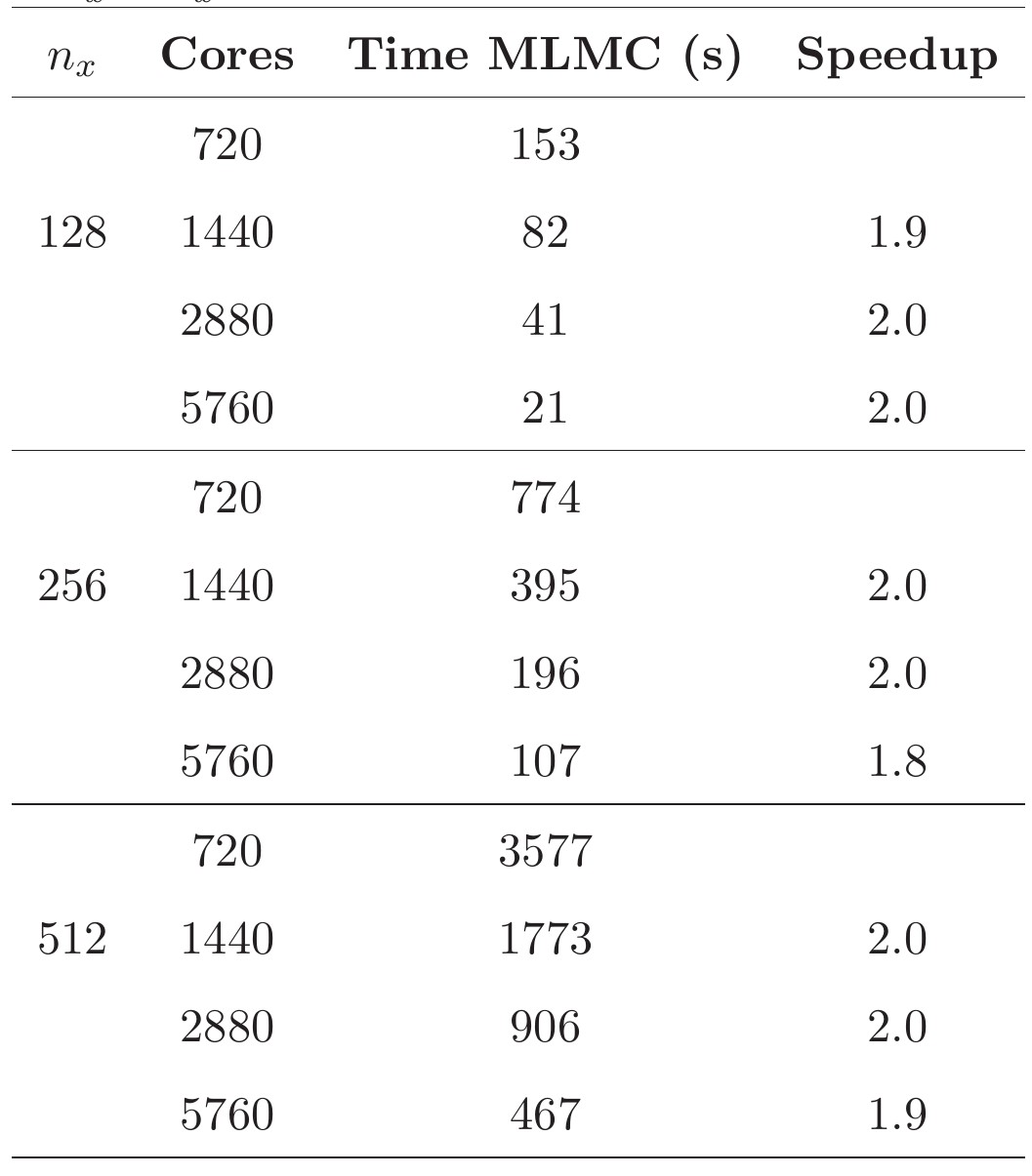
Elapsed time spent for computing the solution of the 3D heat equation at the single point (0,0,0), and for time t=1 as a function of the number of cores. The matrix size for the system is given by nx3 x nx3. Selected publications
|

 POSTDOC position NOW OPEN!
POSTDOC position NOW OPEN!