Aula 9

1  Resumo da matéria

1.1  Matrizes

Muitas vezes é necessário guardar e manipular conjuntos de variáveis do mesmo tipo.  Se fosse necessário, por exemplo, calcular a média de três valores de vírgula flutuante introduzidos pelo utilizador dum programa e escrever cada um desses valores dividido pela média calculada, ter-se-ia de escrever: 
#include <iostream>
using namespace std;
int main()
{
    // Leitura:
    cout << "Introduza três valores: ";
    double a, b, c;
    cin >> a >> b >> c;
    // Cálculo da média:
    double média = (a + b + c) / 3.0;

    // Divisão pela média:
    a /= média;
    b /= média;
    c /= média;
    // Escrita do resultado:
    cout << a << ' ' << b << ' ' << c << endl;
}
Se se pretendesse dividir, já não três, mas 100 ou mesmo 1000 valores pela sua média, esta abordagem seria no mínimo pouco elegante, já que seriam necessárias tantas variáveis quantos os valores a ler do teclado.  A linguagem C++ resolve este tipo de problemas fornecendo o conceito de matriz (array em inglês): uma matriz é um agregado de elementos do mesmo tipo que podem ser indexados por valores inteiros.  Cada elemento duma matriz pode ser interpretado e usado como outra variável qualquer.  A conversão do programa acima para ler 1000 em vez de três valores seria: 
#include <iostream>
using namespace std;
int main()
{
    const int número_de_valores = 1000;
    // Leitura:
    cout << "Introduza " << número_de_valores << " valores: ";
    double valores[número_de_valores];  // definição da matriz com
                                        // 1000 double.
    for(int i = 0; i < número_de_valores; i++)
        cin >> valores[i];         // lê o i-ésimo valor do teclado.
    // Cálculo da média:
    double soma = 0.0;
    for(int i = 0; i < número_de_valores; i++)
        soma += valores[i];        // acrescenta o i-ésimo valor à soma.
    double média = soma / número_de_valores;
    // Divisão pela média:
    for(int i = 0; i < número_de_valores; i++)
        valores[i] /= média;       // divide o i-ésimo valor pela média.
    // Escrita do resultado:
    for(int i = 0; i < número_de_valores; i++)
        cout << valores[i] << ' '; // escreve o i-ésimo valor.
}
Note-se a utilização duma constante para representar o número de valores a processar.  Alterar o programa para processar não 1000 mas 10000 valores é, neste caso, trivial: basta redefinir a constante.  A alternativa seria fazer substituições automáticas no texto do programa, o que poderia ter consequências desastrosas se o valor literal 1000 fosse utilizado no programa num contexto diferente.

1.1.1  Definição de matrizes

Para utilizar uma matriz de variáveis é necessário defini-la*.  A sintaxe da definição de matrizes em C++ é simples:
tipo nome[número_de_elementos];
em que tipo é o tipo de cada elemento da matriz, nome é o nome da matriz, e número_de_elementos é o número de elementos da nova matriz.  Por exemplo: 
int mi[10];    // matriz com 10 int.
char mc[80];   // matriz com 80 char.
float mf[20];  // matriz com 20 float.
double md[3];  // matriz com 3 double.
O número de elementos de uma matriz tem de ser um valor constante (i.e., um valor literal ou uma constante*).  Não é possível (para já) criar uma matriz usando um número de elementos variável.  Mas é possível (e em geral aconselhável) usar constantes em vez de valores literais: 
int n = 50;
const int m = 100;
int matriz_de_inteiros[m];   // ok, m é uma constante.
int matriz_de_inteiros[300]; // ok, 300 é um valor literal.
int matriz_de_inteiros[n];   // errado, n não é uma constante.
Tal como se fez uma analogia entre variáveis e folhas de papel nas quais se pode apenas escrever um valor, pode-se também fazer uma analogia entre matrizes e blocos de notas com um número fixo de folhas de papel.

* Ou melhor, é necessário que ela esteja declarada, podendo a sua definição estar noutro local.
* Constantes são entidades definidas com o qualificador const.  Por exemplo: 

const int número_máximo_de_alunos = 1000;
define uma constante inteira (int) de nome número_máximo_de_alunos e valor 1000.

1.1.2  Indexação de matrizes

Seja a definição 
int m[10];
Para atribuir o valor 5 ao sétimo elemento da matriz pode-se escrever: 
m[6] = 5;   // atribui o inteiro 5 ao 7º elemento da matriz.
Ao valor 6, colocado entre [], chama-se índice  Ao escrever o nome duma matriz seguido de [] com um determinado índice está-se a efectuar uma operação de indexação.  Os índices das matrizes são sempre números inteiros e começam sempre em zero.  Assim, o primeiro elemento da matriz m é m[0], o segundo m[1], e assim sucessivamente.  Como é óbvio, os índices usados para aceder às matrizes não necessitam de ser constantes: podem-se usar variáveis, como aliás se pode verificar no exemplo da leitura de 1000 valores.  Assim, o exemplo anterior pode-se escrever: 
int a = 6;
m[a] = 5;   // atribui o inteiro 5 ao 7º elemento da matriz.
Usando de novo a analogia das folhas de papel, uma matriz é como um bloco de notas em que as folhas são numeradas a partir de 0 (zero).  Ao se escrever m[6] = 5, está-se a dizer algo como "substitua-se o valor que está escrito na folha 6 (a sétima) do bloco m pelo valor 5".  Abaixo mostra-se uma representação gráfica da matriz m depois da atribuição:
Gráfico de matriz

Porventura uma das maiores deficiências da linguagem C++ está no tratamento das matrizes, particularmente na indexação.  Por exemplo, o código seguinte não resulta em qualquer erro de compilação nem tão pouco na terminação do programa com uma mensagem de erro: 

int a1 = 0;
int m[4];
int a2 = 0;
m[4] = 1;  // erro! só se pode indexar de 0 a 3!
cout << a1 << ' ' << a2 << endl;
mas o que aparece provavelmente escrito no ecrã é, em alguns compiladores, 
0 1
ou, noutros compiladores, 
1 0
dependendo da arrumação que o compilador dá às variáveis a1, m e a2 na memória.  Esta é uma fonte muito frequente de erros no C++, pelo que se recomenda extremo cuidado na utilização de matrizes.  Uma vez que muitos ciclos usam matrizes, este é mais um argumento a favor do desenvolvimento disciplinado de ciclos.

1.1.3  Inicialização de matrizes

Tal como para as variáveis simples, também as matrizes só são inicializadas implicitamente quando são estáticas.  Matrizes automáticas, i.e., locais a alguma função (e sem o qualificador static) não são inicializadas: os seus elementos contêm inicialmente valores arbitrários (vulgo lixo).  Mas é possível inicializar explicitamente as matrizes.  Para isso, colocam-se os valores com que se pretende inicializar os elementos da matriz entre {}, por ordem e separados por vírgulas.  Por exemplo: 
int m[4] = {10, 20, 0, 0};
O C++ permite ainda que se especifiquem menos valores de inicialização do que o número de elementos da matriz.  Nesse caso, os elementos não inicializados são automaticamente inicializados com 0 (zero).  Ou seja, 
int m[4] = {10, 20};
tem o mesmo efeito que a primeira inicialização.  Pode-se aproveitar este comportamento obscuro para forçar a inicialização duma matriz inteira com zeros: 
int grande[100] = {0}; // inicializa TODA a matriz com 0 (zero).
Mas, como este comportamento é tudo menos óbvio, recomenda-se que se comentem bem tais utilizações.

Por outro lado, o C++ permite que, quando a inicialização é explícita, se omita a dimensão da matriz, sendo esta calculada a partir do número de inicializadores.  Por exemplo: 

int m[] = {10, 20, 0, 0};
tem o mesmo efeito que as definições anteriores.

1.1.3  Matrizes multidimensionais

Em C++ não existe o conceito de matrizes multidimensionais.  Mas a sintaxe de definição de matrizes permite a definição de matrizes cujos elementos são outras matrizes, o que acaba por ter o mesmo efeito prático.  Assim, a definição: 
int m[3][4];
é interpretada como significando int (m[3])[4], o que significa "m é uma matriz com três elementos, cada um dos quais é uma matriz com quatro elementos inteiros".  Ou seja, graficamente:

Embora sejam na realidade matrizes de matrizes, é usual interpretarem-se como matrizes multidimensionais (de resto, será esse o termo usado daqui em diante).  Por exemplo, a matriz m acima é interpretada como:

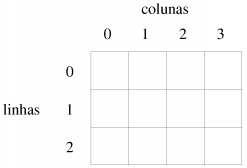
A indexação destas matrizes faz-se usando tantos índices quantas as "matrizes dentro de matrizes" (incluindo a exterior), ou seja, tantos índices quantas as dimensões da matriz.  Para m conforme definida acima: 

m[1][3] = 4;       // atribui 4 ao elemento na linha 1, coluna 3 da matriz.
int i = 0, j = 0;
m[i][j] = m[1][3]; // atribui 4 à posição (0,0) da matriz.

1.1.4  Matrizes como parâmetros de funções

É possível usar matrizes como parâmetros de funções.  O programa para o cálculo da média poderia ser modularizado de modo a usar funções e procedimentos do seguinte modo: 
#include <iostream>
using namespace std;
const int número_de_valores = 1000;
// Procedimento: preenche a matriz com valores lidos do teclado:
void lêMatriz(double m[número_de_valores])
{
    for(int i = 0; i < número_de_valores; i++)
        cin >> m[i];         // lê o i-ésimo elemento do teclado.
}
// Função: devolve a média dos valores na matriz:
double médiaDaMatriz(double m[número_de_valores])
{
    double soma = 0.0;
    for(int i = 0; i < número_de_valores; i++)
        soma += m[i];        // acrescenta o i-ésimo elemento à soma.
    return soma / número_de_valores;
}
// Procedimento: divide todos os valores por divisor:
void normalizaMatriz(double m[número_de_valores], double divisor)
{
    for(int i = 0; i < número_de_valores; i++)
        m[i] /= divisor;     // divide o i-ésimo elemento.
}
// Procedimento: escreve todos os valores no ecrã:
void escreveMatriz(double m[número_de_valores])
{
    for(int i = 0; i < número_de_valores; i++)
        cout << m[i] << ' '; // escreve o i-ésimo elemento.
}
int main()
{
    // Leitura:
    cout << "Introduza " << número_de_valores << " valores: ";
    double valores[número_de_valores];  // definição da matriz com
                                        // 1000 double.
    lêMatriz(valores);
    // Cálculo da média:
    double média = médiaDaMatriz(valores);
    // Divisão pela média:
    normalizaMatriz(valores, média);
    // Escrita do resultado:
    escreveMatriz(valores);
}

Passagens por referência

Para o leitor mais atento o programa acima tem, aparentemente, um erro.  É que, nos procedimentos onde se alteram os valores da matriz (nomeadamente LêMatriz() e NormalizaMatriz()), a matriz parece ser passada por valor e não por referência, visto que não existe na declaração dos parâmetros qualquer & (ver Passagem de argumentos por valor e por referência).  O que acontece é que o C++ passa todas as matrizes por referência e o & é, portanto, redundante*.  Assim, os dois procedimentos referidos alteram de facto a matriz que lhes é passada como argumento.

Esta é uma característica desagradável do C++, porque introduz uma excepção à semântica das chamadas de funções e procedimentos.  Mantém-se no C++ esta característica porque o C++ pretende manter compatibilidade com versões antigas da linguagem, que a herdaram do C.

* Mas poder-se-ia ter explicitado a referência escrevendo void LêMatriz(double (&m)[número_de_valores]) (os () são fundamentais), muito embora isso não seja recomendado, pois sugere que na ausência do & a passagem se faz por valor, o que não é verdade.

Dimensão das matrizes parâmetro

Outra característica do C++ que pode causar alguma confusão tem a ver com o facto de a dimensão das matrizes ser ignorada pelo compilador em parâmetros de funções ou procedimentos.  Esta característica está relacionada com o facto de o C++ não verificar a validade dos índices em operações de indexação, e com o facto de estarem proíbidas a maior parte das operações sobre matrizes tratadas como um todo (ver Restrições na utilização de matrizes).  Assim, para o compilador de C++, LêMatriz(double m[número_de_valores]) e LêMatriz(double m[]) têm exactamente o mesmo significado.

Este facto pode ser usado a favor do programador (se ele tiver cuidado), pois permite-lhe escrever procedimentos e funções que operam sobre matrizes de dimensão arbitrária, desde que a dimensão das matrizes seja também passada como argumento*.  Assim, na versão do programa que se segue todas as funções e procedimentos se tornaram genéricos, o que lhes permite trabalhar com matrizes de dimensão arbitrária: 

#include <iostream>
using namespace std;
// Procedimento: preenche a matriz com n valores lidos do teclado:
void lêMatriz(double m[], int n)
{
    for(int i = 0; i < n; i++)
        cin >> m[i];         // lê o i-ésimo elemento do teclado.
}
// Função: devolve a média dos n valores na matriz:
double médiaDaMatriz(double m[], int n)
{
    double soma = 0.0;
    for(int i = 0; i < n; i++)
        soma += m[i];        // acrescenta o i-ésimo elemento à soma.
    return soma / n;
}
// Procedimento: divide todos os valores por divisor:
void normalizaMatriz(double m[n], int n, double divisor)
{
    for(int i = 0; i < n; i++)
        m[i] /= divisor;     // divide o i-ésimo elemento.
}
void escreveMatriz(double m[n], int n)
{
    for(int i = 0; i < n; i++)
        cout << m[i] << ' '; // escreve o i-ésimo elemento.
}
int main()
{
    const int número_de_valores = 1000;
    // Leitura:
    cout << "Introduza " << número_de_valores << " valores: ";
    double valores[número_de_valores];  // definição da matriz com
                                        // 1000 double.
    lêMatriz(valores, número_de_valores);
    // Cálculo da média:
    double média = médiaDaMatriz(valores, número_de_valores);
    // Divisão pela média:
    normalizaMatriz(valores, número_de_valores, média);
    // Escrita do resultado:
    escreveMatriz(valores, número_de_valores);
}
* Na realidade o valor passado como argumento não precisa de ser o tamanho real da matriz: basta que seja menor ou igual ao tamanho real da matriz.  Isto permite processar apenas parte duma matriz.
O caso das matrizes multidimensionais
É de notar que a linguagem C++ ignora apenas a primeira dimensão das matrizes declaradas como parâmetros de funções ou procedimentos.  Assim é impossível escrever 
double determinante(double m[][], int linhas, int colunas)
{
    // ...
}
com a esperança de definir uma função para calcular o determinante duma matriz bi-dimensional de dimensões arbitrárias...  É obrigatório indicar as dimensões de todas as matrizes excepto a "maior": 
double determinante(double m[][10], int linhas)
{
    // ...
}
Ou seja, a flexibilidade neste caso resume-se a que a função pode trabalhar com um número arbitrário de linhas*.

* Na realidade nem isso, porque o determinante duma matriz só está definido para matrizes quadradas...

1.1.5 Restrições na utilização de matrizes

Para além das incongruências e restrições já referidas relativamente à utilização de matrizes em C++, existem outras restrições que é importante conhecer.

Devolução de matrizes em funções

Não é possível devolver matrizes (directamente) em funções.  Esta restrição desagradável obriga à utilização de procedimentos para processamento de matrizes.

Operações proibidas

Também não são permitidas as atribuições ou comparações entre matrizes.  Esse tipo de operações têm de ser feitas através da aplicação sucessiva dessas operações a cada um dos elementos da matriz.

1.2  Algumas notas sobre quantificadores

Apresentam-se aqui algumas notas sobre quantificadores que são úteis para a construção de condições representativas de estados dos programas, por exemplo, para especificar uma CO (Condição Objectivo).  A notação utilizada encontra-se no Apêndice A.

1.2.1  Somas

O quantificador soma corresponde ao usual somatório.  Na notação utilizada, (S i : m <= i < n : f(i)) tem exactamente o mesmo significado que o somatório (representado pela letra sigma maiúscula, impossível de escrever em HTML) de f(i) com i variando entre m e n (exclusivé).  Por exemplo, é um facto conhecido que (S i : 0 <= i < n : i ) = n (n - 1) / 2 se n >= 0 e (S i : 0 <= i < n : i ) = 0 se n < 0.

Se se pretendesse escrever a condição objectivo duma função que calcula a soma dos n primeiros números ímpares (sendo n um parâmetro da função), poder-se-ia começar por escrever o corpo (quase) vazio da função, colocando no seu início a PC (pré-condição) e no seu final, antes da devolução do resultado, a CO (condição objectivo):

int somaÍmpares(int n)
{
    // PC: n >= 0 e n = n
    int soma;

    // CO: soma = (S i : 0 <= i < n : 2 i + 1) e n = n
    return soma;
}

Note-se que o predicado n = n se encontra tanto na PC como na CO, o que significa que se deseja que n não mude de valor ao longo da função, já que é igual à variável matemática n (que o C++ não tem poderes para alterar...) no início e no fim da função.  Este tipo de restrição, por ser tão obviamente necessário, deixará de ser escrito nas condições de aqui em diante.

1.2.2  Produtos

O quantificador produto corresponde ao produto de termos por vezes conhecido como produtório.  Na notação utilizada, (P i : m <= i < n : f(i)) tem exactamente o mesmo significado que o usual produto (representado pela letra pi maiúscula, impossível de escrever em HTML) de f(i) com i variando entre m e n (exclusivé).  Por exemplo, a definição de factorial é n! = (P i : 1 <= i <= n : i ) se n >= 0.

Se se pretendesse escrever a condição objectivo duma função que calcula o factorial de n (sendo n um parâmetro da função), poder-se-ia escrever:

int factorial(int n)
{
    // PC: n >= 0
    int resultado;

    // CO: resultado = (P i : 1 <= i <= n : i)
    return resultado;
}

1.2.3  Conjunções e o quantificador universal

O quantificador universal corresponde à conjunção de vários predicados usualmente conhecida por "qualquer que seja"*.  Na notação utilizada, (Q i : m <= i < n : p(i)) tem exactamente o mesmo significado que a conjunção das proposições p(i) com i variando entre m e n (exclusivé).  Por exemplo, a definição da função (matemática!) primo(n), que tem valor V se n é primo e F no caso contrário, é: assumindo que % é a operação resto da divisão inteira (como em C++).

Se se pretendesse escrever a condição objectivo duma função (agora em C++) que devolve o valor lógico verdadeiro quando n (sendo n um parâmetro da função) é um número primo, e falso no caso contrário, poder-se-ia escrever:

bool éPrimo(int n)
{
    // PC: n >= 0
    bool é_primo;

    // CO: é_primo = ((Q i : 1 < i < n : n % i <> 0) e n > 1)
    return é_primo;
}

* Se não é claro para si, pense no significado de escrever "todos os humanos têm cabeça".  A tradução para linguagem (quase) matemática seria "qualquer que seja h pertencente ao conjunto dos humanos, h tem cabeça".  Como o conjunto dos humanos é finito, podemos escrever por extenso, listando todos os possíveis humanos: "o Yeltsin (aparenta) ter cabeça e o Sampaio tem cabeça e ...".  Isto é, a conjunção de todas as afirmações.

1.2.4  Disjunções e o quantificador existencial

O quantificador existencial corresponde à disjunção de vários predicados usualmente conhecida por "existe pelo menos um".  Na notação utilizada, (E i : m <= i < n : p(i)) tem exactamente o mesmo significado que a disjunção das proposições p(i) com i variando entre m e n (exclusivé).

Este quantificador está estreitamente relacionado com o quantificador universal.  É sempre verdade que ~ (Q i : m <= i < n : p(i)) = (E i : m <= i < n : ~ p(i)), ou seja, se não é verdade que para qualquer i p(i) é verdadeira, então existe pelo menos um i para o qual p(i) é falsa.  Aplicado à definição de número primo acima, temos ~ primo(n) = ~ (Q i : 1 < i < n : n % i <> 0) = (E i : 1 < i < n : n % i = 0), para n > 1.  I.e., um número maior do que 1 não é primo se for divisível por algum inteiro maior do que 1 e menor que ele próprio.

Se se pretendesse escrever a condição objectivo duma função que devolve o valor lógico verdadeiro quando um valor k existe numa matriz m com n elementos (sendo k, m e n parâmetros da função), e falso no caso contrário, poder-se-ia escrever:

bool existeNaMatrix(int k, int m[], int n)
{
    // PC: n >= 0
    bool existe;

    // CO: existe = (E i : 0 <= i < n : m[i] = k)
    return existe;
}

1.2.5  Contagens

O quantificador de contagem (N i : m <= i < n : p(i)) tem como valor (inteiro) o número de predicados p(i) verdadeiros para i na gama indicada.  Por exemplo, (N i : 1 <= i < 10 : primo(i)) = 4, ou seja, "existem quatro primos entre 1 e 9", é uma afirmação verdadeira.

Este quantificador é extremamente útil quando é necessário especificar condições em que o número de ordem é fundamental.  Se se pretendesse escrever a condição objectivo duma função que devolve o índice da segunda ocorrência de um dado valor k numa matriz m com n elementos (sendo k, m e n parâmetros da função), assumindo que k ocorre pelo menos duas vezes na matriz, poder-se-ia escrever:

int índiceDoSegundo(int k, int m[], int n)
{
    // PC: n >= 2 e (N i : 0 <= i < n : m[i] = k) >= 2
    int índice;

    // CO: (N i : 0 <= i < índice : m[i] = k) = 1 e m[índice] = k
    return existe;
}

O resto da divisão

Quando se apresentou o operador %, resto da definição inteira, não se fez uma definição formal dele.  Esta pode ser feita à custa de alguns dos quantificadores apresentados.  Seja m % n = resto(m, n) (com m >= 0 e n > 0).  Então, resto(m, n) é o único elemento do conjunto {r : 0 <= r < n e (E : q >= 0 : m = qn + r)}.  Claro que a definição está incompleta enquanto não se demonstrar que de facto o conjunto tem um único elemento, ou seja que, quando m >= 0 e n > 0, se tem (N r : 0 <= r < n : (E : q >= 0 : m = qn + r)) = 1.  Essa demonstração deixa-se como exercício para o leitor.

1.3  Algoritmos com matrizes

A título de exemplo desenvolvem-se nesta secção quatro algoritmos, em quatro funções, operando com matrizes: um para calcular a soma dos elementos duma matriz, outro para encontrar o índice do seu maior elemento (ou de um dos seus maiores elementos), outro para verificar se os elementos duma matriz estão todos dentro dum dado intervalo, e o último para encontrar o índice da segunda ocorrência de um dado valor numa matriz.

No desenvolvimento dos algoritmos que se seguem não se insiste em que as variáveis correspondentes aos parâmetros não podem mudar de valor.  Em todo o rigor, no entanto, dever-se-iam incluir condições que o garantissem.

1.3.1  Soma dos elementos de uma matriz

O objectivo é calcular a soma dos valores dos primeiros n elementos duma matriz m.  O primeiro passo consiste em escrever o corpo da função.  Como é necessário no final devolver a soma dos elementos, define-se logo uma variável soma para guardar o seu valor:
int soma(int m[], int n)
{
    int soma;
    // Aqui ficará o algoritmo propriamente dito.
    return soma;
}
O passo seguinte é escrever a pré-condição e a condição objectivo.  Este passo é fundamental, pois consiste em especificar o problema sem quaisquer ambiguidades.  Neste caso as condições são ambas simples, pelo que se apresentam sem comentários:
int soma(int m[], int n)
{
    // PC: n >= 0
    int soma;
    // ...
    // CO: soma = (S k : 0 <= k < n : m[k])
    return soma;
}
O passo seguinte consiste em, tendo percebido que a solução passará forçosamente por um ciclo, determinar uma condição invariante apropriada.  Neste caso pode-se simplesmente substituir o limite superior (constante, pois n não muda de valor ao longo do ciclo) do somatório por uma variável i inteira, acrescentando uma gama de valores apropriada para a mesma.  Assim,
int soma(int m[], int n)
{
    // PC: n >= 0
    int soma;
    int i;
    inic
    // CI: soma = (S k : 0 <= k < i : m[k]) e 0 <= i <= n
    while(G) {
        passo
    }
    // CO: soma = (S k : 0 <= k < n : m[k])
    return soma;
}
Identificada a CI, é necessário escolher uma guarda G tal que seja possível demonstrar que CI e ~ G => CO.  Ou seja, escolher uma G que, quando o ciclo terminar, conduza à CO*.  Neste caso é evidente que a escolha correcta para ~ G é i = n, ou seja, G: i <> n.  Logo:
int soma(int m[], int n)
{
    // PC: n >= 0
    int soma;
    int i;
    inic
    // CI: soma = (S k : 0 <= k < i : m[k]) e 0 <= i <= n
    while(i != n) {
        passo
    }
    // CO: soma = (S k : 0 <= k < n : m[k])
    return soma;
}
De seguida deve-se garantir, por escolha apropriada das instruções de inicialização inic, que a CI é verdadeira no início do ciclo.  Como sempre, devem-se escolher as instruções mais simples que conduzem à veracidade de CI.  Neste caso, é simples verificar que se deve inicializar i com zero e soma também com zero (lembre-se de que a soma de zero elementos é, por definição, zero).  Ou seja:
int soma(int m[], int n)
{
    // PC: n >= 0
    int soma = 0;
    int i = 0;
    // CI: soma = (S k : 0 <= k < i : m[k]) e 0 <= i <= n
    while(i != n) {
        passo
    }
    // CO: soma = (S k : 0 <= k < n : m[k])
    return soma;
}
Como se pretende que o algoritmo termine, deve-se agora escolher um progresso que o garanta (passo é normalmente dividida em duas partes, o progresso prog e a acção acção).  Sendo i inicialmente zero, e sendo n >= 0, é evidente que uma simples incrementação da variável i conduzirá forçosamente à falsidade da G e portanto à terminação do ciclo:
int soma(int m[], int n)
{
    // PC: n >= 0
    int soma = 0;
    int i = 0;
    // CI: soma = (S k : 0 <= k < i : m[k]) e 0 <= i <= n
    while(i != n) {
        acção
        i++;
    }
    // CO: soma = (S k : 0 <= k < n : m[k])
    return soma;
}
Finalmente, é necessário construir uma acção que garanta a veracidade da CI depois do passo, apesar do progresso.  Sabe-se que CI e G são verdadeiras antes do passo, logo:
CI e G: soma = (S k : 0 <= k < i : m[k]) e 0 <= i <= n e i <> n
donde
soma + m[i] = (S k : 0 <= k < i : m[k]) + m[i] e 0 <= i < n
e
soma + m[i] = (S k : 0 <= k < i + 1 : m[k]) e 1 <= i + 1 < n + 1
ou seja,
soma + m[i] = (S k : 0 <= k < i + 1 : m[k]) e 1 <= i + 1 <= n
que implica
soma + m[i] = (S k : 0 <= k < i + 1 : m[k]) e 0 <= i + 1 <= n
que, depois da acção
soma = soma + m[i];
e do progresso já escolhido, resulta de novo na CI, conforme pretendido.  Assim, a função completa é:
int soma(int m[], int n)
{
    // PC: n >= 0
    int soma = 0;
    int i = 0;
    // CI: soma = (S k : 0 <= k < i : m[k]) e 0 <= i <= n
    while(i != n) {
        soma += m[i];
        i++;
    }
    // CO: soma = (S k : 0 <= k < n : m[k])
    return soma;
}
Que se pode ainda escrever, usando a instrução for, como:
// PC: n >= 0
// CO: soma = (S k : 0 <= k < n : m[k])
int soma(int m[], int n)
{
    // CI: soma = (S k : 0 <= k < i : m[k]) e 0 <= i <= n
    int soma = 0;
    for(int i = 0; i != n; i++)
        soma += m[i];
    return soma;
}
Neste último caso colocaram-se PC e CO antes do cabeçalho da função, porque são estas condições que dizem o que a função faz, enquanto se manteve CI como um comentário antes do ciclo, pois é muito importante para a sua compreensão (embora, neste caso particular, por tão simples, talvez se pudesse eliminá-lo).  A CI no fundo reflecte o como o ciclo, e a função, funcionam, ao contrário da PC e da CO, que se referem àquilo que o ciclo, ou a função, faz.

Note-se que o algoritmo desenvolvido corresponde a parte da função médiaDaMatriz() usada em exemplos anteriores.

* Não esquecer que CI é válida no início, durante, e no final do ciclo (por isso se chama condição invariante), e que, quando o ciclo termina, tem de se ter forçosamente que a G é falsa, ou seja, que ~ G é verdadeira.

1.3.2  Índice do maior elemento de uma matriz

O objectivo é construir uma função que devolva um dos índices do máximo valor contido nos primeiros  n elementos duma matriz m.  Como não se especifica qual dos índices devolver caso existam vários elementos com o valor máximo, arbitra-se que se devolve o primeiro desses índices.  Assim:
int índiceDoMáximo(int m[], int n)
{
    // PC: n > 0
    int índice;
    // ...
    // CO: 0 <= índice < n e (Q k : 0 <= k < n : m[k] <= m[índice])
          e (Q k : 0 <= k < índice : m[k] < m[índice])
    return índice;
}
Ou seja, índice tem de pertencer à gama de índices válido para a matriz, o valor de m em índice tem de ser maior ou igual aos valores de todos os elementos da matriz (estas condições garantem que índice é um dos índices do valor máximo na matriz) e os valores dos elementos com índice menor do que índice têm de ser estritamente menores que o valor em índice (ou seja, índice é o primeiro dos índices do valor máximo na matriz).  Note-se que a PC, neste caso, impõe que n não pode ser zero, pois não tem sentido falar do máximo dum conjunto vazio.

É evidente que a procura do primeiro máximo duma matriz tem de recorrer a um ciclo.  Os dois primeiros passos da construção de um ciclo, obtenção da CI e da G, neste caso, são indênticos aos do exemplo anterior (substituição de n por i):

int índiceDoMáximo(int m[], int n)
{
    // PC: n > 0
    int índice;
    int i;
    inic
    // CI: 0 <= índice < i e (Q k : 0 <= k < i : m[k] <= m[índice])
    //    e (Q k : 0 <= k < índice : m[k] < m[índice]) e 0 <= i <= n
    while(i != n) {
        passo
    }
    // CO: 0 <= índice < n e (Q k : 0 <= k < n : m[k] <= m[índice])
          e (Q k : 0 <= k < índice : m[k] < m[índice])
    return índice;
}
Ou seja, a variável índice contém sempre o índice do primeiro elemento cujo valor é o máximo dos valores contidos nos i primeiros elementos da matriz.

A inicialização a usar também é simples, embora desta vez não se possa inicializar i com 0, pois nesse caso não se poderia atribuir qualquer valor a índice!   Assim, a solução é inicializar i com 1 e índice com 0.  Analisando os termos da CI um a um, verifica-se que:

  1. 0 <= índice < i: é verdadeira.
  2. (Q k : 0 <= k < i : m[k] <= m[índice]): como k só pode tomar o valor 0, é também verdadeira.
  3. (Q k : 0 <= k < índice : m[k] < m[índice]): como k não pode tomar qualquer valor, o quantificador tem, por definição, o valor verdadeiro.
  4. 0 <= i <= n: é verdadeira porque a PC obriga n a ser maior que 0.
Esta inicialização é necessária porque não existe máximo dum conjunto vazio, pelo que é necessário inicializar i com 1 e não com 0.

O passo seguinte é a construção do progresso.  Mais uma vez usa-se a simples incrementação de i em cada passo, que conduz forçosamente à terminação do ciclo.  Ou seja, colocando a inicialização e o progresso que se escolheram:

int índiceDoMáximo(int m[], int n)
{
    // PC: n > 0
    int índice = 0;
    int i = 1;
    // CI: 0 <= índice < i e (Q k : 0 <= k < i : m[k] <= m[índice]) e
    //   (Q k : 0 <= k < índice : m[k] < m[índice]) e 0 <= i <= n
    while(i != n) {
        acção
        i++;
    }
    // CO: 0 <= índice < n e (Q k : 0 <= k < n : m[k] <= m[índice])
          e (Q k : 0 <= k < índice : m[k] < m[índice])
    return índice;
}

A parte mais interessante deste exemplo é a que falta: que acção se deve utilizar para manter a condição invariante verdadeira apesar do progresso?  Antes do passo tem-se:

CI e G:  0 <= índice < i e (Q k : 0 <= k < i : m[k] <= m[índice])
      e (Q k : 0 <= k < índice : m[k] < m[índice]) e 0 <= i <= n e i <> n
ou seja
CI e G:  0 <= índice < i e (Q k : 0 <= k < i : m[k] <= m[índice])
      e (Q k : 0 <= k < índice : m[k] < m[índice]) e 0 <= i < n
donde
CI e G:  0 <= índice < i < i + 1 e (Q k : 0 <= k < i : m[k] <= m[índice])
      e (Q k : 0 <= k < índice : m[k] < m[índice]) e 1 <= i + 1 <= n
o que implica
 
CI e G:  0 <= índice < i < i + 1 e (Q k : 0 <= k < i : m[k] <= m[índice])
      e (Q k : 0 <= k < índice : m[k] < m[índice]) e 0 <= i + 1 <= n
Quais os casos possíveis?  Suponha-se que m[i] <= m[índice].  Então
CI e G:  0 <= índice < i + 1 e (Q k : 0 <= k < i : m[k] <= m[índice])
      e m[i] <= m[índice] e (Q k : 0 <= k < índice : m[k] < m[índice])
      e 0 <= i + 1 <= n
ou seja
CI e G:  0 <= índice < i + 1 e (Q k : 0 <= k < i + 1 : m[k] <= m[índice])
      e (Q k : 0 <= k < índice : m[k] < m[índice]) e 0 <= i + 1 <= n
pelo que o progresso não invalida o invariante.  E no caso contrário, se m[i] > m[índice]?  Nesse caso, sendo índice' uma nova variável inicializada com i,conclui-se que
0 <= índice < índice' < i + 1
e (Q k : 0 <= k < i : m[k] <= m[índice] < m[índice']) e m[i] = m[índice']
e (Q k : 0 <= k < índice' : m[k] < m[índice']) e 0 <= i + 1 <= n
onde o segundo quantificador se obteve directamente do primeiro, por substituição de i por índice' e por restrição do número de termos*.  Ou seja
0 <= índice' < i + 1 e (Q k : 0 <= k < i + 1 : m[k] <= m[índice'])
e (Q k : 0 <= k < índice' : m[k] < m[índice']) e 0 <= i + 1 <= n
pelo que a CI se recupera facilmente, neste caso, atribuindo a índice o valor índice' (que é igual a i).  Assim, e eliminando a variável índice', que não é necessária, se  m[i] > m[índice] a CI recupera-se usando a instrução:
índice = i;
 ou seja, a acção é uma instrução alternativa
if(m[i] <= m[índice])
    ; // não é necessário fazer nada.
else
    índice = i;
que se pode simplificar para uma instrução condicional
if(m[i] > m[índice])
    índice = i;
A ideia é que, quando se atinge um elemento com valor maior do que aquele que se julgava até então ser máximo, deve-se actualizar o índice do máximo.

O algoritmo fica então:

int índiceDoMáximo(int m[], int n)
{
    // PC: n > 0
    int índice = 0;
    int i = 1;
    // CI: 0 <= índice < i e (Q k : 0 <= k < i : m[k] <= m[índice])
    //    e (Q k : 0 <= k < índice : m[k] < m[índice]) e 0 <= i <= n
    while(i != n) {
        if(m[i] > m[índice])
            índice = i;
        i++;
    }
    // CO: 0 <= índice < n e (Q k : 0 <= k < n : m[k] <= m[índice])
       e (Q k : 0 <= k < índice : m[k] < m[índice])
    return índice;
}
ou, utilizando um for
// PC: n > 0
// CO: 0 <= índice < n e (Q k : 0 <= k < n : m[k] <= m[índice])
      e (Q k : 0 <= k < índice : m[k] < m[índice])
int índiceDoMáximo(int m[], int n)
{
    int índice = 0;
    // CI: 0 <= índice < i e (Q k : 0 <= k < i : m[k] <= m[índice])
    //    e (Q k : 0 <= k < índice : m[k] < m[índice]) e 0 <= i <= n
    for(int i = 1; i != n; i++)
        if(m[i] > m[índice])
            índice = i;
    return índice;
}
* Só é possível reduzir o número de termos porque se trata duma conjunção.  Note-se que é sempre verdade que p e q => p, pelo que (Q k : m <= k < n : p(k)) => (Q k : m <= k < n' : p(k)) desde que n' <= n.

1.3.3  Elementos de uma matriz num intervalo

Pretende-se escrever uma função que devolva o valor lógico verdadeiro se e só se os valores dos n primeiros elementos duma matriz m estão entre mínimo e máximo (inclusivé).  Neste caso a estrutura da função, a PC e a CO são mais fáceis de escrever:
bool dentroDaGama(int m[], int n, int mínimo, int máximo)
{
    // PC: n >= 0
    bool dentro;
    // ...
    // CO: dentro = (Q k : 0 <= k < n : mínimo <= m[k] e m[k] <= máximo)
    return dentro;
}
De novo a CI e a G são fáceis de determinar (substituição de n por i):
bool dentroDaGama(int m[], int n, int mínimo, int máximo)
{
    // PC: n >= 0
    bool dentro;
    int i;
    inic
    // CI: (dentro = (Q k : 0 <= k < i : mínimo <= m[k] e m[k] <= máximo))
          e 0 <= i <= n
    while(i != n) {
        passo
    }
    // CO: (dentro = (Q k : 0 <= k < n : mínimo <= m[k] e m[k] <= máximo))
    return dentro;
}
A inicialização neste caso pode-se fazer atribuindo zero a i, o que resulta num conjunto vazio de valores possíveis para k no quantificador da CI, pelo que este tem, por definição, o valor V.  Ou seja, deve-se também inicializar dentro com V.  O progresso, pelas mesmas razões que nos exemplos anteriores, corresponde simplesmente a incrementar i:
bool dentroDaGama(int m[], int n, int mínimo, int máximo)
{
    // PC: n >= 0
    bool dentro = true;
    int i = 0;
    // CI: (dentro = (Q k : 0 <= k < i : mínimo <= m[k] e m[k] <= máximo))
          e 0 <= i <= n
    while(i != n) {
        acção
        i++;
    }
    // CO: (dentro = (Q k : 0 <= k < n : mínimo <= m[k] e m[k] <= máximo))
    return dentro;
}
Que acção escolher para recuperar a validade da CI apesar do progresso escolhido?  Antes do passo do ciclo temos
CI e G: (dentro = (Q k : 0 <= k < i : mínimo <= m[k] e m[k] <= máximo))
      e 0 <= i <= n e i <> n
donde
(dentro = (Q k : 0 <= k < i : mínimo <= m[k] e m[k] <= máximo)) e 0 <= i < n
ou seja
(dentro = (Q k : 0 <= k < i : mínimo <= m[k] e m[k] <= máximo))
e 1 <= i + 1 < n + 1
o que implica que
(dentro = (Q k : 0 <= k < i : mínimo <= m[k] e m[k] <= máximo))
e 0 <= i + 1 <= n
Aplicando o predicado mínimo <= m[i] e m[i] <= máximo a ambos os termos da igualdade, tem-se
((dentro e (mínimo <= m[i] e m[i] <= máximo)) =
  ((Q k : 0 <= k < i : mínimo <= m[k] e m[k] <= máximo)
    e (mínimo <= m[i] e m[i] <= máximo))) e 0 <= i + 1 <= n
ou seja
((dentro e (mínimo <= m[i] e m[i] <= máximo)) =
  (Q k : 0 <= k < i + 1 : mínimo <= m[k] e m[k] <= máximo))
e 0 <= i + 1 <= n
pelo que a CI se recupera facilmente usando a acção (onde os parênteses são redundantes, dada a precedência dos operadores em C++)
dentro = (dentro && mínimo <= m[i] && m[i] <= máximo);
A função fica então:
bool dentroDaGama(int m[], int n, int mínimo, int máximo)
{
    // PC: n >= 0
    bool dentro = true;
    int i = 0;
    // CI: (dentro = (Q k : 0 <= k < i : mínimo <= m[k] e m[k] <= máximo))
          e 0 <= i <= n
    while(i != n) {
        dentro =
            dentro && mínimo <= m[i] && m[i] <= máximo;
        i++;
    }
    // CO: (dentro = (Q k : 0 <= k < n : mínimo <= m[k] e m[k] <= máximo))
    return dentro;
}

Reforço da guarda

No ciclo desenvolvido, a variável dentro começa por tomar o valor V, e vai sendo actualizada ao longo dos passos do ciclo.  A observação da instrução correspondente à acção revela que, se a variável dentro alguma vez passar a ter o valor F, então tê-lo-á até ao fim do ciclo, visto F ser o elemento absorvente da conjunção.  Assim, torna-se evidente que todos os passos do ciclo posteriores não têm qualquer utilidade.  Ou seja, o ciclo deve terminar imediatamente quando dentro possuir o valor F.  Ou seja, deve-se reforçar a guarda para
G': dentro e i <> n
(Note-se que é inútil escrever dentro = V.)

Para garantir, agora duma forma mais formal, que o ciclo termina apropriadamente, tem de se verificar se CI e ~ G' => CO.  Mas

CI e ~ G': (dentro = (Q k : 0 <= k < i : mínimo <= m[k] e m[k] <= máximo))
        e 0 <= i <= n e (~ dentro ou i = n)
donde
((dentro = (Q k : 0 <= k < i : mínimo <= m[k] e m[k] <= máximo))
  e 0 <= i <= n e ~ dentro)
ou
((dentro = (Q k : 0 <= k < i : mínimo <= m[k] e m[k] <= máximo))
  e 0 <= i <= n e i = n)
A segunda disjunção implica obviamente CO.  E a primeira?  Sendo ~ dentro verdadeira, conclui-se, da primeira igualdade, que ~ (Q k : 0 <= k < i : mínimo <= m[k] e m[k] <= máximo) é verdadeira, ou seja, (E k : 0 <= k < i : m[k] < mínimo <=  ou máximo < m[k]), donde se conclui que (Q k : 0 <= k < n : mínimo <= m[k] e m[k] <= máximo) só pode ser falsa, e portanto
CO: (dentro = (Q k : 0 <= k < n : mínimo <= m[k] e m[k] <= máximo))
é verdadeira.  Ou seja, pode-se escrever o ciclo como:
bool dentroDaGama(int m[], int n, int mínimo, int máximo)
{
    // PC: n >= 0
    bool dentro = true;
    int i = 0;
    // CI: (dentro = (Q k : 0 <= k < i : mínimo <= m[k] e m[k] <= máximo))
          e 0 <= i <= n
    while(dentro && i != n) {
        dentro = dentro && mínimo <= m[i] && m[i] <= máximo;
        i++;
    }
    // CO: (dentro = (Q k : 0 <= k < n : mínimo <= m[k] e m[k] <= máximo))
    return dentro;
}
que se pode simplificar para
// PC: n >= 0
// CO: (dentro = (Q k : 0 <= k < n : mínimo <= m[k] e m[k] <= máximo))
bool dentroDaGama(int m[], int n, int mínimo, int máximo)
{
    // CI: dentro = (Q k : 0 <= k < i : mínimo <= m[k] e m[k] <= máximo)
          e 0 <= i <= n
    bool dentro = true;
    for(int i = 0; dentro && i != n; i++)
        dentro = dentro && mínimo <= m[i] && m[i] <= máximo;
    return dentro;
}
Mas o ciclo pode ser simplificado.  Uma observação atenta revela que, no início de cada passo do ciclo, por G ser forçosamente verdadeira, a variável dentro é V, logo, por V ser o elemento neutro da conjunção, a acção pode-se simplificar, obtendo-se
// PC: n >= 0
// CO: (dentro = (Q k : 0 <= k < n : mínimo <= m[k] e m[k] <= máximo))
bool dentroDaGama(int m[], int n, int mínimo, int máximo)
{
    // CI: dentro = (Q k : 0 <= k < i : mínimo <= m[k] e m[k] <= máximo)
          e 0 <= i <= n
    bool dentro = true;
    for(int i = 0; dentro && i != n; i++)
        dentro = mínimo <= m[i] && m[i] <= máximo;
    return dentro;
}

1.3.4  Segundo elemento de uma matriz com um dado valor

O objectivo agora é encontrar o índice do segundo elemento com valor k numa matriz m com n elementos.  Neste caso a PC é um pouco mais complicada, pois tem de se garantir que existem pelo menos dois elementos com o valor pretendido, o que, por si só, implica que a matriz tem de ter pelo menos dois elementos.  A CO é mais simples.  Diz que o índice a devolver deve corresponder a um elemento com valor k e que no conjunto dos elementos com índice menor existe apenas um elemento com valor k (diz ainda que o índice deve ser válido, neste caso maior do que 0, porque têm de existir pelo menos dois elementos com valores iguais até ao índice).

int índiceDoSegundo(int k, int m[], int n)
{
    // PC: n >= 2 e (N i : 0 <= i < n : m[i] = k) >= 2
    int índice;
    // ...
    // CO: (N i : 0 <= i < índice : m[i] = k) = 1 e m[índice] = k e 0 < índice < n
    return índice;
}

Neste caso não existe na CO qualquer quantificador onde se possa substituir (com sucesso) uma constante por uma variável (note-se n é considerada uma constante, como habitualmente).  Assim, a determinação da CI pode ser tentada factorizando a CO, que é uma conjunção, em CI e ~ G.  Uma observação atenta das condições revela que a escolha apropriada é

CI: (N i : 0 <= i < índice : m[i] = k) = 1 e  0 < índice < n
~ G: m[índice] = k
Assim, pode-se escrever:
int índiceDoSegundo(int k, int m[], int n)
{
    // PC: n >= 2 e (N i : 0 <= i < n : m[i] = k) >= 2
    int índice;
    inic
    // CI: (N i : 0 <= i < índice : m[i] = k) = 1 e  0 < índice < n
    while(m[índice] != k) {
        passo
    }
    // CO: (N i : 0 <= i < índice : m[i] = k) = 1 e m[índice] = k
    return índice;
}
Um problema com a escolha que se fez para a CI é que, aparentemente, não é fácil fazer a inicialização.  Assume-se daqui em diante que a inicialização está feita (ver E a inicialização?).  O passo seguinte, portanto, é determinar o passo do ciclo.  Antes do passo tem-se CI e G, ou seja:
CI e G: (N i : 0 <= i < índice : m[i] = k) = 1 e  0 < índice < n e m[índice] <> k
Mas
(N i : 0 <= i < índice : m[i] = k) = 1 e m[índice] <> k
é o mesmo que
(N i : 0 <= i < índice + 1 : m[i] = k) = 1
porque, sendo m[índice] <> k, pode-se estender a gama de valores de i sem afectar a contagem de afirmações verdadeiras.

De 0 < índice < n é imediato que 1 < índice + 1 <= n, o que implica que 0 < índice + 1 <= n.  Admita-se que índice + 1 = n.  Nesse caso teríamos, pelo que vimos anteriormente, que

(N i : 0 <= i < n : m[i] = k) = 1
Mas esta afirmação é falsa, de acordo com a PC!  Logo, conclui-se que índice + 1 < n.  Ou seja,
(N i : 0 <= i < índice + 1 : m[i] = k) = 1 e 0 < índice + 1 < n
Mas isto significa que se pode incrementar índice sem com isso afectar a validade da CI.  Repare-se que, neste caso, passo resume-se a uma única instrução: índice++.  Será que ela garante que o ciclo termina?  É óbvio que sim, porque se índice pudesse crescer o suficiente para atingir n, teríamos, da PC, que (N i : 0 <= i < n : m[i] = k) = 2, pelo que em alguma altura anterior teria de ser válida a CO.  Logo, o ciclo termina com índice < n.

Em suma, a função pode-se escrever:

int índiceDoSegundo(int k, int m[], int n)
{
    // PC: n >= 2 e (N i : 0 <= i < n : m[i] = k) >= 2
    int índice;
    inic
    // CI: (N i : 0 <= i < índice : m[i] = k) = 1 e  0 < índice < n
    while(m[índice] != k) {
        índice++;
    }
    // CO: (N i : 0 <= i < índice : m[i] = k) = 1 e m[índice] = k
    return índice;
}

E a inicialização?

A inicialização do ciclo anterior é um problema por si só, com as mesmas pré-condições, mas com uma outra condição objectivo igual à condição invariante do ciclo já desenvolvido.  Isto é, o problema a resolver é:
// PC: n >= 2 e (N i : 0 <= i < n : m[i] = k) >= 2
int índice;
inic
// CO' = CI: (N i : 0 <= i < índice : m[i] = k) = 1 e  0 < índice < n
Ou seja, pretende-se que índice seja maior do que o índice da primeira ocorrência de k na matriz.  A solução para este problema é mais simples se se restringir a condição objectivo um pouco mais.  Em particular, pode-se impor que índice seja o índice imediatamente após a primeira ocorrência de k.  Isto é:
// PC: n >= 2 e (N i : 0 <= i < n : m[i] = k) >= 2
int índice;
inic
// CO'': (N i : 0 <= i < índice : m[i] = k) = 1 e m[índice - 1] =  k e 0 < índice < n
// => CI: (N i : 0 <= i < índice : m[i] = k) = 1 e  0 < índice < n
ou ainda, se se terminar com uma incrementação de índice:
// PC: n >= 2 e (N i : 0 <= i < n : m[i] = k) >= 2
int índice;
inic
// CO''': (N i : 0 <= i < índice + 1: m[i] = k) = 1 e m[índice] =  k e 0 <= índice < n
índice++;
// => CO'': (N i : 0 <= i < índice : m[i] = k) = 1 e m[índice - 1] =  k e 0 < índice < n
// => CI: (N i : 0 <= i < índice : m[i] = k) = 1 e  0 < índice < n
Mas isso é o mesmo que dizer
// PC: n >= 2 e (N i : 0 <= i < n : m[i] = k) >= 2
int índice;
inic
// CO''': (N i : 0 <= i < índice: m[i] = k) = 0 e m[índice] =  k e 0 <= índice < n
índice++;
// => CI: (N i : 0 <= i < índice : m[i] = k) = 1 e  0 < índice < n
Como (N i : 0 <= i < índice: m[i] = k) = 0 é o mesmo que (Q i : 0 <= i < índice: m[i] <> k), temos
// PC: n >= 2 e (N i : 0 <= i < n : m[i] = k) >= 2
int índice;
inic
// CO''': (Q i : 0 <= i < índice: m[i] <> k) e m[índice] =  k e 0 <= índice < n
índice++;
// => CI: (N i : 0 <= i < índice : m[i] = k) = 1 e  0 < índice < n
Ou seja, a inicialização reduz-se ao problema de encontrar o índice do primeiro elemento com valor k!  A solução deste problema passa pela construção de um outro ciclo e é relativamente simples, pelo que se apresenta a solução sem mais comentários:
// PC: n >= 2 e (N i : 0 <= i < n : m[i] = k) >= 2
int índice = 0;
// CI': (Q i : 0 <= i < índice : m[i] <> k) e  0 <= índice < n
while(m[índice] != k)
    índice++;
// CO''': (Q i : 0 <= i < índice: m[i] <> k) e m[índice] =  k e 0 <= índice < n
índice++;
// => CI: (N i : 0 <= i < índice : m[i] = k) = 1 e  0 < índice < n
Concluindo, a função completa é:
// PC: n >= 2 e (N i : 0 <= i < n : m[i] = k) >= 2
// CO: (N i : 0 <= i < índice : m[i] = k) = 1 e m[índice] = k
int índiceDoSegundo(int k, int m[], int n)
{
    int índice = 0;
    // CI': (Q i : 0 <= i < índice : m[i] <> k) e  0 <= índice < n
    while(m[índice] != k)
        índice++;
    índice++;
    // CI: (N i : 0 <= i < índice : m[i] = k) = 1 e  0 < índice < n
    while(m[índice] != k)
        índice++;
    return existe;
}
Uma solução genérica poderia ser desenvolvida reconhecendo que o código anterior é repetitivo:
// PC: n >= i > 0 e (N l : 0 <= l < n : m[l] = k) >= i
// CO: (N l : 0 <= l < índice : m[l] = k) = i - 1 e m[índice] = k
int índiceDoIésimo(int k, int m[], int n, int i)
{
    int índice = -1;
    for(int j = 0; j < i; j++)
        índice++;
        // CI': (N i : 0 <= i < índice : m[i] = k) = j e  0 <= índice < n
        while(m[índice] != k)
            índice++;
    return índice;
}
Qual será a CI do ciclo exterior (o for)?

2  Exercícios

1. Construa uma função ou procedimento que, dada uma matriz m de inteiros com n elementos (entre parênteses, a PC a impor):

a)  Inverta a ordem dos valores na matriz (n >= 0).
b)  Verifique se os valores dos elementos estão por ordem (não estritamente) crescente (n >= 0, pois sequências com 0 ou 1 elementos estão, por definição, por qualquer ordem que se deseje).
c)  Devolva o índice da primeira ocorrência de um valor k, sabendo que ele existe na matriz (logo n > 0).
d)  Devolva o índice da primeira ocorrência de um valor k, se o valor não existir deve devolver n (n >= 0).
e)  Devolva o maior valor existente na matriz (n > 0).  Pode usar alguma função já desenvolvida?
f)  Devolva o maior valor existente na matriz e calcule o número de vezes que ocorre (n > 0).  Use referências para guardar o número de ocorrências calculado.

3  Exercícios propostos

1. Construa uma função ou procedimento que, dada uma matriz m de inteiros com n elementos (entre parênteses, a PC a impor):

a)  Verifique se os valores dos elementos são todos iguais (n >= 0, pois sequências com 0 ou 1 elementos são, por definição, constantes).
b)  Verifique se os valores dos elementos estão por ordem estritamente crescente (n >= 0, pois sequências com 0 ou 1 elementos estão, por definição, por qualquer ordem que se deseje).
c)  Verifique se os valores dos elementos estão por ordem crescente ou decrescente, ou seja, se a sequência de elementos é monótona (n >= 0, pois sequências com 0 ou 1 elementos são, por definição, monótonas).
d)  (Difícil) Devolva o índice de uma ocorrência de um valor k, sabendo que ele existe na matriz (logo n > 0) e sabendo que os valores na matriz estão por ordem crescente.  Como pode tirar partido da ordenação da matriz?
e)  (Difícil) Desloque todos os valores de m posições para a direita circularmente, i.e., se os valores saírem à direita, entram à esquerda (n > 0). Como resolver sem impor restrições a m?  Como resolver sem restrições em m e com uma única variável auxiliar?
f)  Sendo um "planalto" uma sequência contígua de valores idênticos, devolva o comprimento do planalto mais longo na matriz (n >= 0).

2.a)  Crie uma função que calcule a norma de um vector de 10 float.  Faça um pequeno programa para testar esta função.
2.b)  Crie uma função que normalize um vector de 10 float.  Normalizar consiste em dividir cada um dos componentes pela norma do vector.  Faça um pequeno programa para testar esta função.

3.  Crie uma função que calcule o produto interno de dois vectores de float.  Faça um pequeno programa para testar esta função.

4.  Crie uma função que preencha uma matriz a de 10 por 10 elementos inteiros de tal forma que o elemento ai,j da matriz tenha o valor ij.  Faça um pequeno programa para testar esta função.