Quase todas as resoluções de problemas envolvem tomadas
de decisões e repetições. Dificilmente se consegue
encontrar um algoritmo interessante que não envolva, quando lido
em português, as palavras 'se' e 'enquanto', correspondendo aos conceitos
de selecção ou alternativa e de iteração ou
repetição. Neste capítulo estudar-se-ão
os mecanismos que a linguagem C++ fornece para suportar esses conceitos
e discutir-se-ão metodologias de resolução de problemas
usando esses mecanismos.
Suponha-se que se pretendia desenvolver uma função para calcular o valor absoluto de um inteiro. O "esqueleto" da função pode ser o que se segue
/*Este esqueleto inclui, como habitualmente, os comentário iniciais que clarificam o que a função faz, o cabeçalho que indica como a função se utiliza, e um corpo, onde se colocarão as instruções que resolvem o problema, i.e., que explicitam como a função funciona.
Esta função devolve o valor absoluto do argumento.
PC: (sem restrições)
CO: absoluto = |x|, ou seja, absoluto >= 0 e (absoluto = -x ou absoluto = x)
*/
int absoluto(int x)
{
...
}
A resolução deste problema requer que sejam tomadas acções diferentes consoante o valor de x seja positivo ou negativo (ou nulo). São portanto fundamentais as chamadas instruções de selecção ou alternativa.
if(x < 0) // 1as linhas 1 a 4 correspondem a uma única instrução de selecção ou alternativa.. Esta instrução de selecção é composta de uma condição (na linha 1) e duas instruções controladas (linhas 2 e 4). Se x for menor do que zero quando a instrução if é executada, então a próxima instrução a executar é a instrução na linha 2, passando o valor de x a ser zero. No caso contrário, se x for maior ou igual a zero, a próxima instrução a executar é a instrução na linha 4, passando a variável x a ter o valor 1. Em qualquer dos casos, a execução continua na linha 5 *.
x = 0; // 2
else // 3
x = 1; // 4
... // 5
Como a instrução na linha 2 só é executada se x < 0, diz-se que x < 0 é a sua guarda, normalmente representada por G. De igual modo, a guarda da instrução na linha 4 é x >= 0. A guarda da instrução controlada após o else está implícita, podendo ser obtida por negação da guarda do if: ¬(x < 0) é equivalente a x >= 0. Assim, numa instrução de selecção pode-se sempre inverter a ordem das instruções controladas desde que se negue a condição. Por exemplo,
if(x < 0)é equivalente a
// G1: x < 0
x = 0;
else
// G2: x >= 0
x = 1;
if(x >= 0)Em certos casos pretende-se apenas executar uma dada instrução se determinada condição se verificar, não se desejando fazer nada caso a condição seja falsa. Nestes casos pode-se omitir o else e a instrução que se lhe segue. Por exemplo, no troço de programa
// G2: x >= 0
x = 1;
else
// G1: x < 0
x = 0;
if(x < 0) // 1se x for menor do que zero, então é executada a instrução controlada na linha 2, passando o valor de x a ser zero, sendo em seguida executada a instrução na linha 3 *. No caso contrário a execução passa directamente para a linha 3.
x = 0; // 2
... // 3
A este tipo restrito de instrução de selecção também se chama instrução condicional. Uma instrução condicional é sempre equivalente a uma instrução de selecção em que a instrução após o else é uma instrução nula (a instrução nula corresponde em C++ a um simples terminador ;). Ou seja, o exemplo anterior é equivalente a:
if(x < 0) // 1Em muitos casos é necessário executar condicionalmente não uma instrução simples mas sim uma sequência de instruções. Para o conseguir, agrupam-se essas instruções num bloco de instruções ou instrução composta, colocando-as entre chavetas {}. Por exemplo, o código que se segue ordena os valores guardados nas variáveis x e y de tal modo que x termine com um valor menor ou igual ao de y:
x = 0; // 2a
else // 2b
; // 2c
... // 3
int x, y;* Se existirem instruções return, break, continue ou goto nas instruções controladas pelo if, o fluxo normal de execução pode ser alterado de tal modo que a execução não continua na instrução imediatamente após o if.
...
if(x > y) {
int t = x;
x = y;
y = t;
}
int a, minimo, maximo;Note-se que, sendo as instruções de selecção instruções por si só, o teste acima se pode escrever sem recurso às chavetas, ou seja,
cin >> minimo >> maximo >> a;if(a < minimo)
cout << a << " menor que mínimo." << endl;
else {
if(a <= maximo)
cout << a << " entre mínimo e máximo." << endl;
else
cout << a << " maior que máximo." << endl;
}
if(a < minimo)Em casos como este, em que se encadeiam if else sucessivos, é comum usar uma indentação que deixa mais claro que existem mais do que duas alternativas,
cout << a << " menor que mínimo." << endl;
else
if(a <= maximo)
cout << a << " entre mínimo e máximo." << endl;
else
cout << a << " maior que máximo." << endl;
if(a < minimo)
cout << a << " menor que mínimo." << endl;
else if(a <= maximo)
cout << a << " entre mínimo e máximo." << endl;
else
cout << a << " maior que máximo." << endl;
if(a < minimo)Fica claro que as guardas não correspondem directamente à condição indicada no if respectivo, com excepção da primeira guarda.
// G1: a < mínimo
cout << a << " menor que mínimo." << endl;
else if(a <= maximo)
// G2: mínimo <= a e a <= máximo
cout << a << " entre mínimo e máximo." << endl;
else
// G3: mínimo <= a e máximo < a
cout << a << " maior que máximo." << endl;
As n guardas de uma instrução de selecção, construída com n - 1 instruções if encadeadas, podem ser obtidas a partir das condições de cada um dos if como se segue:
if(C1)Ou seja, as guardas das instruções controladas são obtidas por conjunção da condição do if respectivo com a negação das guardas das instruções controladas (ou das condições de todos os if) anteriores na sequência, com seria de esperar.
// G1: C1
...
else if(C2)
// G2: ¬G1 e C2 (ou seja, ¬C1eC2)
...
else if(C3)
// G3: ¬G1 e ¬G2 e C3 (ou seja, ¬C1 e ¬C2eC1)
...
...
else if(Cn-1)
// Gn-1: ¬G1 e ... e ¬Gn-2eCn-1 (ou seja, ¬C1e ... e ¬Cn-2eCn-1)
...
else
// Gn: ¬G1 e ... e ¬Gn-2e ¬Gn-1 (ou seja, ¬C1e ... e ¬Cn-1)
...
// PC: mínimo < máximo
if(a < minimo)
// G1: a < mínimo
cout << a << " menor que mínimo." << endl;
else if(a <= maximo)
// G2: mínimo <= a e a <= máximo
cout << a << " entre mínimo e máximo." << endl;
else
// G3: máximo < a
cout << a << " maior que máximo." << endl;
if(m == 0)o else não diz respeito ao primeiro if. Ao contrário do que a indentação do código sugere, o else diz respeito ao segundo if. Em caso de dúvida, um else pertence ao if mais próximo (e acima...) dentro mesmo bloco de instruções e que não tenha já o respectivo else. Para corrigir o exemplo anterior é necessário construir uma instrução composta, que neste caso consiste de uma única instrução de selecção
if(n == 0)
cout << "m e n são zero." << endl;
else
cout << "m não é zero." << endl;
if(m == 0) {Para evitar erros deste tipo, é conveniente usar blocos de instruções de uma forma liberal, pois construções como a que se apresentou podem dar origem a erros muito difíceis de detectar e corrigir. Os compiladores de boa qualidade, no entanto, avisam o programador da presença de semelhantes (aparentes) ambiguidades.
if(n == 0)
cout << "m e n são zero." << endl;
} else
cout << "m não é zero." << endl;
Um outro erro frequente corresponde a colocar um ; logo após a condição do if ou logo após o else. Por exemplo, a intenção do programador do troço de código
if(x < 0);era provavelmente que se mantivesse o valor de x excepto quando este fosse negativo. Mas a interpretação feita pelo compilador (e a correcta dada a sintaxe da linguagem C++) é
x = 0;
if(x < 0)ou seja, x terminará sempre com o valor zero! Este tipo de erro, não sendo muito comum, é ainda mais difícil de detectar do que o da (suposta) ambiguidade da pertença de um else: os olhos do programador, habituados que estão à presença de ; no final de cada linha, recusam-se a detectar o erro.
; // instrução nula: não faz nada.
x = 0;
Note-se que nas asserções cada variável pertence a um determinado conjunto. Para as variáveis C++, esse conjunto é determinado pelo tipo da variável indicado na sua definição (e.g., int x; significa que x pertence ao conjunto dos inteiros entre -2n-1 e 2n-1 - 1, se os int tiverem n bits). Para as variáveis matemáticas, esse conjunto deveria, em rigor, ser indicado explicitamente. Neste texto, no entanto, admite-se que as variáveis matemáticas pertencem ao conjunto dos inteiros, salvo onde for explicitamente indicado outro conjunto ou onde o conjunto seja fácil de inferir pelo contexto da asserção. Finalmente, nas asserções é normal assumir que as variável C++ não têm limitações (e.g., admite-se que uma variável int pode guardar qualquer inteiro). Embora isso não seja verdade, permite resolver um grande número de problemas sem que se introduzam demasiados detalhes nas demonstrações.
Em cada ponto de um programa existe um determinado conjunto de variáveis, cada uma das quais pode tomar determinados valores, consoante o seu tipo. Ao conjunto de todos os possíveis valores de todas as variáveis existentes num dado ponto de um programa chama-se o espaço de estados nesse ponto. Ao conjunto dos valores das variáveis existentes num determinado ponto do programa num determinado instante de tempo chama-se o estado de um programa. Assim, o estado de um programa é um elemento do espaço de estados.
++n;onde se admite que a variável n tem inicialmente um valor não-negativo. Como adicionar asserções a este troço de programa? Em primeiro lugar escreve-se a asserção que corresponde à assunção de que n guarda um valor não-negativo:
// n >= 0A asserção que segue uma instrução é tipicamente obtida pela semântica da instrução e pela respectiva pré-condição. Ou seja, dada a PC, a instrução implica a veracidade da respectiva CO. No caso acima é óbvio que
++n;
// n >= 0ou seja, se n era maior ou igual a zero antes da incrementação, depois da incrementação será forçosamente maior ou igual a um.
++n;
// n >= 1
A demonstração informal da correcção de um pedaço de código pode, portanto, ser feita recorrendo a asserções. Suponha-se que se pretende demonstrar que o código
int t = x;troca os valores de duas variáveis x e y do tipo int. Começa-se por escrever as duas principais asserções: a pré-condição e a condição objectivo da sequência completa de instruções. Neste caso a escrita destas asserções é complicada pelo facto de a CO ter de ser referir aos valores das variáveis antes das instruções. Para resolver este problema, considere-se que as variáveis matemáticas x e y representam os valores iniciais das variáveis C++ x e y (note-se bem a diferença de tipo de letra usada para variáveis matemáticas e para variáveis do programa C++). Então a CO pode ser escrita simplesmente como
x = y;
y = t;
// x = y e y = xe a PC como
// x = x e y = ydonde o código com as asserções iniciais e finais é
// x = x e y = yA demonstração de correção pode ser feita deduzindo as asserções intemédias:
int t = x;
x = y;
y = t;
// x = y e y = x
// x = x e y = yA demonstração de correcção pode ser feita também partindo dos objectivos. Para cada instrução, partindo da última, determina-se quais as condições mínimas a impor às variáveis antes da instrução, i.e., determina-se qual a PC mais fraca a impor à instrução em causa, de modo a que, depois dessa instrução, a CO da instrução seja verdadeira.
int t = x;
// x = x e y = yet = x
x = y;
// x = y e y = yet = x
y = t;
// x = y e y = x (e t = x)
// PC = ???a PC mais fraca que, depois da atribuição, conduz à CO, pode ser obtida substituindo todas as ocorrências da variável x na CO por expressão. Esta dedução da PC só pode ser feita se a expressão cujo valor se atribui a x não tiver efeitos laterais, i.e., se não implicar a alteração de nenhuma variável do programa (ver Ordem de cálculo e efeitos laterais).
x = expressão;
// CO
Por exemplo, suponha-se que se pretendia saber qual a PC mais fraca para a qual a instrução de atribuição x = -x; conduz à CO x >= 0. Aplicando o método descrito a
// PC = ???obtém-se
x = -x;
// CO: x >= 0
// PC: -x >= 0, ou seja, x <= 0Ou seja, para que a inversão do sinal de x conduza a um valor não-negativo, o menos que tem de se exigir é que o valor de x seja inicialmente não-positivo.
x = -x;
// CO: x >= 0
Voltando ao exemplo da troca de valores de duas variáveis
int t = x;e aplicando a técnica proposta obtém-se sucessivamente
x = y;
y = t;
// x = y e y = x
int t = x;
x = y;
// x = y e t = x
y = t;
// x = y e y = x
int t = x;
// y = y e t = x
x = y;
// x = y e t = x
y = t;
// x = y e y = x
// y = y e x = xtendo-se recuperado a PC inicial.
int t = x;
// y = y e t = x
x = y;
// x = y e t = x
y = t;
// x = y e y = x
Em geral este método não conduz exactamente à PC escrita inicialmente. Suponha-se que se pretendia demonstrar que
// PC: x < 0Usando o método anterior conclui-se que:
x = -x;
// x >= 0
// PC: x < 0Mas como x < 0 implica que x <= 0, conclui-se que o código está correcto.
// -x >= 0 ou seja, x <= 0
x = -x;
// x >= 0
if(x > y) {Qual a CO e qual a PC? Considerem-se x e y os valores de x e y antes da instrução de selecção. Então a PC e a CO podem ser escritas
int t = x;
x = y;
y = t;
}
// PC: x = x ey = yOu seja, o problema fica resolvido quando as variáveis x e y mantêm ou trocam os seus valores iniciais e x termina com um valor não superior ao de y. Note-se que determinar uma PC não é fácil. A PC e a CO, em conjunto, constituem a especificação formal do problema. A sua escrita obriga à compreensão profunda do problema a resolver, e daí a dificuldade.
if(x > y) {
int t = x;
x = y;
y = t;
}
// CO: x <= y e ((x = x e y = y) ou (x = y e y = x))
Será que a instrução condicional conduz forçosamente da PC à CO? É necessário demonstrá-lo.
É conveniente começar por converter a instrução condicional na instrução de selecção equivalente e, simultaneamente, explicitar as guardas das instruções controladas:
// PC: x = xey = yA PC, sendo verdadeira antes da instrução alternativa, também o será imediatamente antes de qualquer das instruções controladas, pelo que se pode escrever
if(x > y) {
// G1: x > y
int t = x;
x = y;
y = t;
} else
// G2: x <= y
; // instrução nula!
// ??
// PC: x = xey = yPode-se agora deduzir as asserções válidas após cada instrução controlada:
if(x > y) {
// x > y ex = x e y = y
int t = x;
x = y;
y = t;
} else
// x <= y ex = x e y = y
;
// ??
// PC: x = xey = yConclui-se que, depois da troca de valores entre x e y nas instruções controladas pelo if, y > x, ou seja, x < y. Mas x < y implica que x <= y. Logo pode-se deduzir que
if(x > y) {
// x > y ex = x e y = y
int t = x;
// t > y ex = x e y = y e t = x
x = y;
// t > x ex = y e y = y et = x
y = t;
// y > x ex = y e y = x (e t = x)
} else
// x <= y ex = x e y = y
;
// x <= y ex = x e y = y, a instrução nula não afecta as asserções...
// ??
// y > x e x = y e y = xonde a escrita de duas asserções uma após a outra significa que a segunda pode ser deduzida da primeira (ou que a segunda é implicada pela primeira). Usando este facto e eliminando as asserções intermédias, úteis apenas durante a demonstração,
// x <= y e x = y e y = x
// PC: x = xey = yFalta agora deduzir a asserção válida depois da instrução de selecção. Esse ponto (assinalado com // ??) pode ser atingido depois de se ter passado por qualquer uma das instruções alternativas, pelo que a asserção válida é a disjunção das asserções deduzidas para cada uma das instruções alternativas:
if(x > y) {
int t = x;
x = y;
y = t;
// x <= y e x = y e y = x
} else
;
// x <= y ex = x e y = y
// ??
// PC: x = xe y = yque é exactamente a CO que se pretendia demonstrar válida.
if(x > y) {
int t = x;
x = y;
y = t;
// x <= y ex = y e y = x
} else
;
// x <= y ex = x e y = y
// (x <= y e x = y e y = x) ou (x <= yex = x e y = y)
// ou seja,
// x <= y e ((x = y e y = x) ou (x = xey = y))
Mais uma vez seria possível partir dos objectivos durante a demonstração. Neste caso começa por se observar que a CO tem de ser válida no final de qualquer das instruções controladas pela instrução de selecção:
// PC: x = xey = yDepois vão-se determinando sucessivamente as PC mais fracas de cada instrução (do fim para o início) usando as regras descritas acima para as atribuições:
if(x > y) {
// G1: x > y
int t = x;
x = y;
y = t;
// x <= y e ((x = y e y = x) ou (x = x e y = y))
} else
// G2: x <= y
;
// x <= y e ((x = y e y = x) ou (x = x e y = y))
// CO: x <= y e ((x = y e y = x) ou (x = x e y = y))
// PC: x = xey = yEliminando as asserções intermédias obtém-se:
if(x > y) {
// G1: x > y
// y <= x e ((y = y e x = x) ou (y = x e x = y))
int t = x;
// y <= t e ((y = y e t = x) ou (y = x e t = y))
x = y;
// x <= t e ((x = y e t = x) ou (x = x e t = y))
y = t;
// x <= y e ((x = y e y = x) ou (x = x e y = y))
} else
// G2: x <= y
// x <= y e ((x = y e y = x) ou (x = x e y = y))
;
// x <= y e ((x = y e y = x) ou (x = x e y = y))
// CO: x <= y e ((x = y e y = x) ou (x = x e y = y))
// PC: x = xey = yBasta agora verificar se a PC em conjunção com cada uma das guardas implica a asserção respectiva deduzida. Neste caso basta verificar que:
if(x > y) {
// G1: x > y
// y <= x e ((y = y e x = x) ou (y = x e x = y))
int t = x;
x = y;
y = t;
} else
// G2: x <= y
// x <= y e ((x = y e y = x) ou (x = x e y = y))
;
// CO: x <= y e ((x = y e y = x) ou (x = x e y = y))
Em geral, portanto, para demonstrar a correcção de uma instrução de selecção (com n alternativas, ou seja, com n instruções controladas)
// PCseguem-se os seguintes passos:
if(C1)
// G1: C1
instrução1
else if(C2)
// G2: ¬G1e C2
instrução2
else if(C3)
// G3: ¬G1 e ¬G2 e C3
instrução3
...
else if(Cn-1)
// Gn-1: ¬G1 e ... e ¬Gn-2eCn-1
instruçãon-1
else
// Gn: ¬G1 e ... e ¬Gn-1
instruçãon
// CO
Regresse-se ao problema inicial, da escrita de uma função para calcular o valor absoluto de um valor inteiro. O objectivo é, portanto, preencher o corpo da função com "esqueleto"
/*onde se usou o predicado V (verdadeiro) para indicar que a função não tem pré-condições.
Esta função devolve o valor absoluto do argumento.
PC: V (sem restrições)
CO: absoluto = |x|, ou seja, absoluto >= 0 e (absoluto = -x ou absoluto = x)
*/
int absoluto(int x)
{
...
}
Para simplificar o desenvolvimento, pode-se começar o corpo pela definição de uma variável local para guardar o resultado e terminar com a devolução do seu valor, o que permite escrever as asserções principais da função em termos do valor desta variável *:
/*Antes de começar o desenvolvimento, é necessário perceber se para a resolução do problema é necessário recorrer a uma instrução de selecção. Neste caso é óbvio que sim, pois tem de se discriminar entre valores negativos e positivos (e talvez nulos) de x.
Esta função devolve o valor absoluto do argumento.
PC: V
CO: absoluto = |x|, ou seja, absoluto >= 0 e (absoluto = -x ou absoluto = x)
*/
int absoluto(int x)
{
int r;
// PC': V
...
// CO': r >= 0 e (r = -x ou r = x)
return r;
}
O desenvolvimento usado será baseado nos objectivos. Este é um princípio importante da programação [4]: a programação deve ser orientada pelos objectivos. É certo que a pré-condição afecta a solução de qualquer problema, mas os problemas são essencialmente determinados pela condição objectivo. De resto, com se pode verificar depois de alguma prática, mais inspiração para a resolução de um problema pode ser obtida por análise da condição objectivo do que por análise da pré-condição. Por exemplo, é comum não haver qualquer pré-condição na especificação de um problema, donde nesses casos só a condição objectivo poderá ser usada como fonte de inspiração.
* Note-se que a semântica de uma instrução de retorno é muito semelhante à de uma instrução de atribuição, nomeadamente a PC mais fraca pode ser obtida por substituição, na CO da função,do nome da função pela expressão usada na instrução de retorno. Assim, a PC mais fraca da instrução return r; que leva a
CO: absoluto = |x|, ou seja, absoluto >= 0 e (absoluto = -xouabsoluto = x)é
CO: r = |x|, ou seja, r >= 0 e (r = -x ou r = x).No entanto, a instrução de retorno difere da instrução de atribuição numa coisa: a instrução de retorno termina a execução da função.
// ??donde
r = -x;
// CO': r >= 0 e (r = -x ou r = x)
// -x >= 0 e (-x = -x ou -x = x) ou seja, x <= 0 e (V ou x = 0), ou seja, x <= 0Logo, a instrução r = -x; só conduz aos resultados pretendidos desde que x tenha inicialmente um valor não-positivo (PC1: x <= 0).
r = -x;
// CO': r >= 0 e (r = -x ou r = x)
A mesma verificação pode ser feita para a segunda instrução
// ??donde
r = x;
// CO': r >= 0 e (r = -x ou r = x)
// x >= 0 e (x = -xoux = x) ou seja, x >= 0 e (x = 0 ou V), ou seja, x >= 0Logo, a instrução r = x; só conduz aos resultados pretendidos desde que x tenha inicialmente um valor não-negativo (PC2: x >= 0).
r = x;
// CO': r >= 0 e (r = -x ou r = x)
Note-se que, até agora, se determinou o seguinte corpo para a função:
/*
Esta função devolve o valor absoluto do argumento.
PC: V
CO: absoluto = |x|, ou seja, absoluto >= 0 e (absoluto = -x ou absoluto = x)
*/
int absoluto(int x)
{
int r;
// PC': V
if(C1)
// G1: ??
// PC1: x <= 0
r = -x;
else
// G2: ??
// PC2: x >= 0
r = x;
// CO': r >= 0 e (r = -x ou r = x)
return r;
}
/*
Esta função devolve o valor absoluto do argumento.
PC: V
CO: absoluto = |x|, ou seja, absoluto >= 0 e (absoluto = -x ou absoluto = x)
*/
int absoluto(int x)
{
int r;
// PC': V
if(C1)
// G1: x <= 0
r = -x;
else
// G2: x >= 0
r = x;
// CO': r >= 0 e (r = -x ou r = x)
return r;
}
Neste caso a PC' não impõe qualquer restrição, ou seja PC': V. Logo, tem de se verificar se V implicaG1ouG2. Neste caso G1 ouG2 é x <= 0 ou x <= 0, ou seja, V. Como V implica V, o problema está quase resolvido.
/*Note-se que a segunda guarda foi alterada, pois a instrução após o else tem guarda G2 = ¬G1 = x > 0. Esta guarda é mais forte que a guarda originalmente determinada, pelo que a alteração não traz qualquer problema. Na realidade o que aconteceu foi que a semântica da instrução if do C++ forçou à escolha de qual das instruções controladas lida com o caso x = 0.
Esta função devolve o valor absoluto do argumento.
PC: V
CO: absoluto = |x|, ou seja, absoluto >= 0 e (absoluto = -x ou absoluto = x)
*/
int absoluto(int x)
{
int r;
// PC': V
if(x <= 0)
// G1: x <= 0
r = -x;
else
// G2: x > 0
r = x;
// CO': r >= 0 e (r = -x ou r = x)
return r;
}
/*será ela completa? Observe-se a seguinte "solução":
Esta função devolve o valor absoluto do argumento.
PC: V
CO: absoluto = |x|, ou seja, absoluto >= 0 e (absoluto = -x ou absoluto = x)
*/
int absoluto(int x)
{
}
/*Esta função cumpre a CO, embora claramente não resolva o problema satisfatoriamente. Que se passou? O problema está na especificação, que não proíbe mudanças de valor da variável x. É possível deixar clara essa proibição indicando claramente que x não é uma variável mas sim uma constante, o que invalida a "solução" proposta. Voltando à solução inicial e explicitando a impossibilidade de alterar o valor de x, a função é portanto:
Esta função devolve o valor absoluto do argumento.
PC: V
CO: absoluto = |x|, ou seja, absoluto >= 0 e (absoluto = -x ou absoluto = x)
*/
int absoluto(int x)
{
x = 1;
return 1;
}
/*Esta solução pode ser simplificada se se observar que, depois de terminada a instrução de selecção, a função se limita a devolver o valor guardado em r por uma das duas instruções controladas. Assim, é possível eliminar essa variável e devolver imediatamente o valor apropriado:
Esta função devolve o valor absoluto do argumento.
PC: V
CO: absoluto = |x|, ou seja, absoluto >= 0 e (absoluto = -x ou absoluto = x)
*/
int absoluto(const int x)
{
int r;
if(x <= 0)
r = -x;
else
r = x;
return r;
}
/*Por outro lado, se a instrução controlada pelo if termina com uma instrução return, então não é necessária uma instrução de selecção, bastando uma instrução condicional:
Esta função devolve o valor absoluto do argumento.
PC: V
CO: absoluto = |x|, ou seja, absoluto >= 0 e (absoluto = -x ou absoluto = x)
*/
int absoluto(const int x)
{
if(x <= 0)
return -x;
else
return x;
}
/*Este último formato não é forçamente mais claro ou preferível ao anterior, mas é muito comum encontrá-lo em programas escritos em C++.
Esta função devolve o valor absoluto do argumento.
PC: V
CO: absoluto = |x|, ou seja, absoluto >= 0 e (absoluto = -x ou absoluto = x)
*/
int absoluto(const int x)
{
if(x <= 0)
return -x;
return x;
}
Para se verificar na prática a importância da especificação cuidada do problema, tente-se resolver o seguinte problema:
Escreva uma função que, dados dois argumentos do tipo int, devolva o booleano verdadeiro se o primeiro for múltiplo do segundo e falso no caso contrário.Neste ponto o leitor deve parar de ler e tentar resolver o problema.
....................................
A abordagem típica do programador é considerar que um número n é múltiplo de outro m se o resto da divisão de n por m for zero e passar ao código:
bool éMúltiplo(int m, int n)Implementada a função, o programador fornece-a à sua equipa para utilização. Depois de algumas semanas de utilização, o programa em desenvolvimento, na fase de testes, aborta com uma mensagem (ambiente Linux):
{
if(m % n == 0)
return true;
else
return false;
}
Floating exception (core dumped)Depois de umas horas no depurador, conclui-se que, se o segundo argumento da função for zero, a função tenta uma divisão por zero, com a consequente paragem do programa.
Neste ponto o leitor deve parar de ler e tentar resolver o problema.
....................................
Chamado o programador original da função, este observa que não há múltiplos de zero, e portanto tipicamente corrige a função para
bool éMúltiplo(int m, int n)Corrigida a função e integrada de novo no programa em desenvolvimento, e repetidos os testes, não se encontra qualquer erro e o desenvolvimento continua. Finalmente o programa é fornecido ao cliente. O cliente utiliza o programa durante meses até que detecta um problema estranho, incompreensível. Como tem um contrato de manutenção com a empresa que desenvolveu o programa, comunica-lhes o problema. A equipa de manutenção, de que o programador original não faz parte, depois de algumas horas de execução do programa em modo depuração e de tentar reproduzir as condições em que o erro ocorre (que lhe foram fornecidas duma forma parcelar pelo cliente), acaba por detectar o problema: a função devolve false quando lhe são passados dois argumentos zero! Mas zero é múltiplo de zero! Rogando pragas ao programador original da função, esta é corrigida para:
{
if(n != 0)
if(m % n == 0)
return true;
else
return false;
else
return false;
}
bool éMúltiplo(int m, int n)O código é testado e verifica-se que os erros estão corrigidos.
{
if(n != 0)
if(m % n == 0)
return true;
else
return false;
else
if(m == 0)
return true;
else
return false;
}
Depois, o programador olha para o código e acha-o demasiado complicado: para quê as instruções de selecção se uma simples instrução de retorno basta?
Neste ponto o leitor deve parar de ler e tentar resolver o problema com uma única instrução de retorno.
....................................
Basta devolver o resultado duma expressão booleana que reflita os casos em que m é múltiplo de n:
bool éMúltiplo(int m, int n)Como a alteração é meramente cosmética, o programador não volta a testar e o programa corrigido é fornecido ao cliente. Poucas horas depois de ser posto ao serviço o programa aborta. O cliente recorre de novo aos serviços de manutenção, desta vez furioso. A equipa de manutenção verifica rapidamente que a execução da função leva a uma divisão por zero como originalmente. Desta vez a correcção do problema é simples: basta inverter os operandos da primeira conjunção:
{
return (m % n == 0 && n != 0) || (m == 0 && n == 0);
}
bool éMúltiplo(int m, int n)Note-se que esta simples troca corrige o problema porque nos operadores lógicos o cálculo é atalhado, i.e., o operando esquerdo é calculado em primeiro lugar e, se o resultado ficar imediatamente determinado (ou seja, se o primeiro operando numa conjunção for falso ou se o primeiro operando numa disjunção for verdadeiro) o operando direito não chega a ser calculado (ver Secção 2.5.3).
{
return (n != 0 && m % n == 0) || (m == 0 && n == 0);
}
void limita(int& x, int mínimo, int máximo)que limite o valor de x ao intervalo [mínimo, máximo], onde se assume que mínimo <= máximo. I.e., se o valor de x for inferior a mínimo, então deve ser alterado para mínimo, se for superior a máximo, deve ser alterado para máximo, se pertencer ao intervalo deve ser deixado com o valor original.
Como habitualmente, começa por se escrever a especificação do procedimento, onde x é uma variável matemática usada para representar o valor inicial da variável C++ x:
/*A observação da condição objectivo conduz imediatamente às seguintes possíveis instruções controladas:
Este procedimento limita x ao intervalo [mínimo, máximo].
PC: mínimo <= máximo e x = x
CO: (x = xex >= mínimo e x <= máximo) ou (x = mínimo e x <= mínimo) ou
(x = máximoex >= máximo)
*/
void limita(int& x, int mínimo, int máximo)
{
}
; // para manter x com o valor inicial x.
x = mínimo;
x = máximo;As pré-condições mais fracas para que se verifique a CO do procedimento depois de cada uma das instruções são:
// PC1: (x = x e x >= mínimo e x <= máximo) ou (x = mínimoex <= mínimo) oupara a primeira instrução,
(x = máximo e x >= máximo)
; // para manter x com o valor inicial x.
// PC2: (mínimo = x e x >= mínimo e x <= máximo) ou (mínimo = mínimoex <= mínimo) oupara a segunda instrução, e
(mínimo = máximo e x >= máximo)
// ou seja:
// PC2: (mínimo = x e x >= mínimo e x <= máximo) ou x <= mínimoou
(mínimo = máximo e x >= máximo)
x = mínimo;
// PC3: (máximo = x e x >= mínimo e x <= máximo) ou (máximo = mínimoex <= mínimo) oupara a última instrução.
(máximo = máximo e x >= máximo)
// ou seja:
// PC3: (máximo = x e x >= mínimo e x <= máximo) ou (máximo = mínimoex <= mínimo) ou
x >= máximo
x = máximo;
A determinação das guardas faz-se de modo a que PCeGi implique PCi.
No primeiro caso tem-se da PC que x = x, pelo que a guarda mais fraca é:
// G1: (x >= mínimo e x <= máximo) ou (x = mínimo) ou (x =máximo)pois os casos x = mínimo e x = máximo são cobertos pela primeira conjunção dado que a PC garante que mínimo <= máximo.
// ou seja:
// G1: x >= mínimoex <= máximo
No segundo caso, pelas mesmas razões, tem-se que:
// G2: (mínimo = x e x <= máximo) oux <= mínimo oupois a PC mínimo <= máximo obriga a que, sendo x = mínimo, também será x <= máximo.
(mínimo = máximo e x >= máximo)
// ou seja:
// G2: mínimo = x ou x <= mínimo ou (mínimo = máximo e x >= máximo)
// ou seja:
// G2: x <= mínimoou (mínimo = máximo e x >= máximo)
Da mesma forma se obtém:
// G3: (máximo = mínimo e x <= máximo) oux >= máximoÉ evidente que há sempre pelo menos uma destas guardas válidas quaisquer que sejam os valores dos argumentos verificando as PC. Logo, não são necessárias quaisquer outras instruções controladas.
Ou seja, a estrutura da instrução de selecção é (trocando a ordem das instruções de modo a que a instrução nula fique em último lugar):
if(C1)A observação das guardas demonstra que elas são redundantes para algumas combinações de valores. Por exemplo, se mínimo = máximo qualquer das guardas G2 e G3 se verifica. É fácil verificar, portanto, que as guardas podem ser simplificadas (reforçadas) para:
// G2: x <= mínimo ou (mínimo = máximoex >= máximo)
x = mínimo;
else if(C2)
// G3: (máximo = mínimo e x <= máximo) oux >= máximo
x = máximo;
else
// G1: x >= mínimo e x <= máximo
;
if(C1)de modo a que, nesse caso, seja válida apenas uma das guardas (excepto, claro, quando x = mínimo = máximo, em que se verificam de novo as duas). De igual modo se podem eliminar as redundâncias no caso de x ter como valor um dos extremos do intervalo, pois nesse caso a guarda G1 "dá conta do recado":
// G2: x <= mínimo
x = mínimo;
else if(C2)
// G3: x >= máximo
x = máximo;
else
// G1: x >= mínimo e x <= máximo
;
if(C1)
// G2: x < mínimo
x = mínimo;
else if(C2)
// G3: x > máximo
x = máximo;
else
// G1: x >= mínimo e x <= máximo
;
Assim, as condições das instruções if
são:
if(x < mínimo)Finalmente, pode-se eliminar o último else, pelo que o procedimento fica:
// G2: x < mínimo
x = mínimo;
else if(x > máximo)
// G3: x > máximo
x = máximo;
else
// G1: x >= mínimo e x <= máximo
;
/*que pode ser simplificado para
Este procedimento limita x ao intervalo [mínimo, máximo].
PC: mínimo <= máximo e x = x
CO: (x = xex >= mínimo e x <= máximo) ou (x = mínimo e x <= mínimo) ou
(x = máximoex >= máximo)
*/
void limita(int& x, int mínimo, int máximo)
{
if(x < mínimo)
// G2: x < mínimo
x = mínimo;
else if(x > máximo)
// G3: x > máximo
x = máximo;
/*
else
// G1: x >= mínimo e x <= máximo
;
*/
}
/*
Este procedimento limita x ao intervalo [mínimo, máximo].
PC: mínimo <= máximo e x = x
CO: (x = xex >= mínimo e x <= máximo) ou (x = mínimo e x <= mínimo) ou
(x = máximoex >= máximo)
*/
void limita(int& x, int mínimo, int máximo)
{
if(x < mínimo)
x = mínimo;
else if(x > máximo)
x = máximo;
}
/*Será possível simplificá-la mais? Sim. A linguagem C++ fornece um operador ternário (com três operandos), que permite escrever a solução como
Esta função devolve o valor absoluto do argumento.
PC: V
CO: absoluto = |x|, ou seja, absoluto >= 0 e (absoluto = -x ou absoluto = x)
*/
int absoluto(const int x)
{
if(x <= 0)
return -x;
return x;
}
/*Este operador, ? :, tem a seguinte sintaxe:
Esta função devolve o valor absoluto do argumento.
PC: V
CO: absoluto = |x|, ou seja, absoluto >= 0 e (absoluto = -x ou absoluto = x)
*/
int absoluto(const int x)
{
return x <= 0? -x : x;
}
condição ? expressão1 : expressão2O resultado do operador é o resultado da expressão expressão1, se condição for verdadeira (nesse caso expressão2 não chega a ser calculada), ou o resultado da expressão expressão2, se condição for falsa (nesse caso expressão1 não chega a ser calculada).
// CO: surgiu no ecrã a versão por extenso de dígito.Em C++ existe uma solução mais usual para este problema usando a instrução de selecção switch. Quando é necessário comparar uma variável com vários valores possíveis, e executar uma acção diferente em cada um dos casos, deve-se usar esta instrução. O procedimento anterior ficaria:
// PC: 0 <= dígito < 10
void escreveDígitoPorExtenso(int dígito)
{
if(dígito == 0)
cout << "zero";
else if(dígito == 1)
cout << "um";
else if(dígito == 2)
cout << "dois";
else if(dígito == 3)
cout << "três";
else if(dígito == 4)
cout << "quatro";
else if(dígito == 5)
cout << "cinco";
else if(dígito == 6)
cout << "seis";
else if(dígito == 7)
cout << "sete";
else if(dígito == 8)
cout << "oito";
else
cout << "nove";
}
// CO: surgiu no ecrã a versão por extenso de dígito.Esta instrução não permite a especificação de gamas de valores nem de desigualdades: construções como
// PC: 0 <= dígito < 10
void escreveDígitoPorExtenso(int dígito)
{
switch(dígito) {
case 0:
cout << "zero";
break;
case 1:
cout << "um";
break;
case 2:
cout << "dois";
break;
case 3:
cout << "três";
break;
case 4:
cout << "quatro";
break;
case 5:
cout << "cinco";
break;
case 6:
cout << "seis";
break;
case 7:
cout << "sete";
break;
case 8:
cout << "oito";
break;
default:
cout << "nove";
break;
}
}
É possível agrupar várias alternativas:
switch(valor) {Isto acontece porque a construção case n: apenas indica qual o ponto de entrada nas instruções que compõem o switch quando a sua expressão de controlo (entre parênteses após a palavra-chave switch) tem valor n. A execução do corpo do switch (o bloco de instruções entre {}) só termina quando for atingida a chaveta final ou quando for executada uma instrução de break (terminado o switch a execução continua sequencialmente após a chaveta final). A consequência deste facto é que, se no exemplo anterior se eliminarem os break:
case 1:
case 2:
case 3:
cout "1, 2, ou 3";
break;
...
}
// CO: surgiu no ecrã a versão por extenso de dígito.uma chamada escreveDígitoPorExtenso(7) resulta em:
// PC: 0 <= dígito < 10
void escreveDígitoPorExtenso(int dígito)
{
switch(dígito) {
case 0:
cout << "zero";
case 1:
cout << "um";
case 2:
cout << "dois";
case 3:
cout << "três";
case 4:
cout << "quatro";
case 5:
cout << "cinco";
case 6:
cout << "seis";
case 7:
cout << "sete";
case 8:
cout << "oito";
default:
cout << "nove";
}
}
que não é o que se pretendia!seteoitonove
Note-se que, pelas razões que se indicaram atrás, não é possível usar a instrução switch (pelo menos de uma forma imediata) como alternativa a:
// PC: 0 <= valore valor < 10000.A ordem pela qual se fazem as comparações em instruções de selecção encadeadas pode ser muito relevante em termos do tempo de execução do programa, embora seja irrelevante no que diz respeito aos resultados. Suponha-se que os valores passados como argumento a escreveGrandeza() são equiprováveis. Nesse caso consegue-se demostrar que, em média, são necessárias 2,989 comparações ao executar o procedimento e que, invertendo a ordem das instruções controladas para
// CO: surgiu no ecrã a ordem de grandeza de valor.
void escreveGrandeza(double x)
{
if(x < 10)
cout << "unidades";
else if(x < 100)
cout << "dezenas";
else if(x < 1000)
cout << "centenas";
else
cout << "milhares";
}
// PC: 0 <= valore valor < 10000.são necessárias 1,11 comparações (demonstre-o)!
// CO: surgiu no ecrã a ordem de grandeza de valor.
void escreveGrandeza(double x)
{
if(x >= 1000)
cout << "milhares";
else if(x >= 100)
cout << "centenas";
else if(x >= 10)
cout << "dezenas";
else
cout << "unidades";
}
No caso da instrução de selecção switch a ordem é irrelevante desde que todos os conjuntos de instruções tenham o respectivo break.
2. Escreva um programa que, dado um número inteiro entre 0 e 99 o escreva por extenso. Exemplo:
Introduza um número:Se se desejasse que o programa escrevesse
35
O número introduzido foi três dezenas e cinco unidades.
O número introduzido foi trinta e cinco.o que se deveria fazer?
3. Escreva uma função que devolva o número de dias de um mês num dado ano passado como argumento. Lembre-se que os anos múltiplos de 4 são bissextos, com excepção dos múltiplos de 100, mas incluindo os múltiplos de 400 (esta fórmula só é válida para datas ocidentais em geral depois de 1752).
4.a) Faça um programa que, dado um número inteiro que representa a idade de uma pessoa, escreva qual a sua faixa etária. As faixas etárias são definidas do seguinte modo: entre 0 e 12 anos - criança, de 12 a 20 - adolescente, de 20 a 60 - adulto, acima de 60 - idoso.
4.b) Modifique o programa anterior de modo a que seja inserido o sexo da pessoa (m ou f) em questão e as respostas sejam adequadas a esta informação. Por exemplo, se a pessoa em questão for do sexo feminino em vez de escrever "adulto" deve escrever "adulta".
5. Suponha que as letras A, B, C e D foram codificadas em zeros e uns da seguinte forma: A = 0, B = 11, C = 100 e D = 101. Crie um programa que, quando é introduzido um conjunto de zeros e uns apartir do teclado descodifique a primeira letra que aparece. Por exemplo:
Introduza um conjunto de zeros e uns:6. Caso já se sinta apto a usar a noção de ciclo, tente fazer um programa que descodifique toda a cadeia de zeros e uns. Atenção: pode haver sequências que não terminam com a codificação total de um caracter (por exemplo 01 = A?). O seu programa deve estar preparado para lidar com esse tipo de erros do utilizador. Exemplo:
1001001100110
C
Introduza um conjunto de zeros e uns:
10010011001101
CCBAABA?
O conhecimento da sintaxe e da semântica das instruções de iteração do C++ não é suficiente para o desenvolvimento de bom código que as utilize. Por um lado, o desenvolvimento de bom código C++ obriga à demonstração formal ou informal do seu correcto funcionamento. Por outro lado, o desenvolvimento de ciclos não é uma tarefa fácil, sobretudo para o principiante. Assim, na Secção 4.3 apresenta-se um método de demonstração da correcção de ciclos e faz-se uma pequena introdução à metodologia de Dijkstra, que fundamenta e disciplina a construção de ciclos (sem no entanto a mecanizar).
* O adjectivo "recursivo" é um neologismo informático que ainda não consta nos dicionários. Foi construído por analogia com o adjectivo "iterativo" e tem essencialmente o mesmo significado que "recorrente". De acordo com [1], iterar significa "tornar a fazer (...) repetir (...)" enquanto recorrer significa "tornar a correr (...)". Recursão e iteração são, portanto, conceitos semelhantes. Em termos de linguagens de programação, no entanto, envolvem mecanismos diferentes, como se verá. No entanto há relações fortes entre os dois conceitos (ver discussão acerca de como transformar soluções recursivas em soluções iterativas em [2, secção 3.4]).
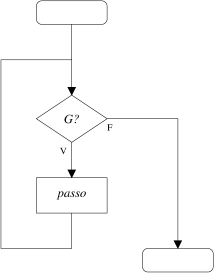
A execução da instrução while consiste na execução repetida da instrução instrução_controlada enquanto espressão_booleana tiver o valor verdadeiro (true). A expressão_booleana é sempre calculada antes da instrução instrução_controlada. Assim, se a expressão for inicialmente falsa (false), a instrução instrução_controlada não chega a ser executada, passando o fluxo de execução para a instrução subsequente ao while. Note-se que a instrução instrução_controlada pode consistir em qualquer instrução do C++, nomeadamente um bloco de instruções ou outro ciclo.while(expressão_booleana) instrução_controlada
À expressão booleana de controlo do while chama-se a guarda do ciclo (representada por G), enquanto à instrução controlada se chama passo. Assim, o passo é repetido enquanto a G for verdadeira. Ou seja
while(G)O fluxo de execução de um programa é muitas vezes mais fácil de representar na forma de um fluxograma ou diagrama de fluxo. Neste diagramas as caixas rectangulares correspondem a instruções (em rigor "processos"), as caixas rômbicas (em forma de losango) correspondem a decisões, e as caixas rectangulares com cantos arredondados marcam o início e o fim do troço de código representado pelo diagrama. As decisões correspondem a pontos da execução em que, dependendo do valor lógico (V ou F) de uma dada condição, a execução pode tomar um de dois caminhas alternativos. A execução da instrução de iteração while pode ser representada pelo seguinte fluxograma:
passo

// PC: n >= 0O fluxograma correspondente é:
// CO: o ecrã contém uma linha adicional com os inteiros de 0 a n exclusivé separados por espaços.
void escreveInteiros(const int n) // 1
{ // 2
int i = 0; // 3
while(i != n) { // 4
cout << i << ' '; // 5
++i; // 6
} // 7
cout << endl; // 8
} // 9
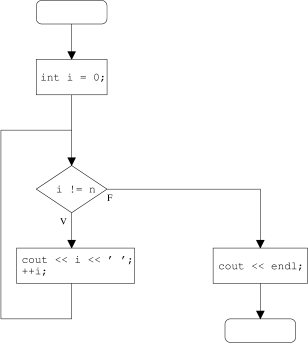
Seguindo o fluxograma, começa por se inicializar a variável i com 0 (linha 3) e em seguida executa-se o ciclo while que:
iniconde inic são as instruções de inicialização (que preparam as variáveis envolvidas no ciclo), prog é uma instrução chamada progresso do ciclo (que garante que o ciclo termina em tempo finito), e acção é a acção do ciclo (ver Correcção total). Nestes ciclos, portanto, o passo subdivide-se em acção e prog.
while(G) {
acção
prog
}
O C++ possui uma outra instrução de iteração, a instrução for, que permite escrever abreviadamente este tipo de ciclos:
for(inic; G; prog)em que inic e prog têm de ser expressões em C++, embora inic possa definir variáveis locais.
acção
O procedimento escreveInteiros() desenvolvido acima pode portanto ser reescrito como:
// PC: n >= 0Note-se que, ao converter o while num for, se aproveitou para restringir ainda mais a visibilidade da variável i que, estando definida no cabeçalho do for, só é visível nessa instrução (linhas 3 e 4). Relembra-se que é de toda a conveniência que a visibilidade das variáveis seja sempre o mais restrita possível à zona onde de facto são necessárias.
// CO: o ecrã contém uma linha adicional com os inteiros de 0 a n exclusivé separados por espaços.
void escreveInteiros(const int n) // 1
{ // 2
for(int i = 0; i != n; ++i) // 3
cout << i << ' '; // 4
cout << endl; // 5
}
Quaisquer das expressões no cabeçalho de uma instrução for (inic, G e prog) pode ser omitida. A omissão da guarda G é equivalente à utilização de uma guarda sempre verdadeira, gerando por isso um ciclo infinito, ou laço (loop). Ou seja, escrever
for(inic; ; prog)é o mesmo que escrever
acção
for(inic; true; prog)cujo fluxograma é:
acção

Este tipo de ciclos só é verdadeiramente interessante se passo contiver alguma instrução return ou break (ver abaixo) que obrigue o ciclo a terminar alguma vez.
Um outro tipo de ciclo em C++ corresponde à instrução dowhile. A sintaxe desta instrução é:
A execução da instrução do while consiste na execução repetida de instrução_controlada enquanto espressão_booleana tiver o valor verdadeiro (true). Mas, ao contrário do que se passa no caso da instrução while, a expressão_booleana é sempre calculada e verificada depois da instrução instrução_controlada. Quando o resultado é falso o fluxo de execução passa para a instrução subsequente ao do while. Note-se que instrução_controlada pode consistir em qualquer instrução do C++, nomeadamente um bloco de instruções.do instrução_controlada while(expressão_booleana);
Tal como no caso da instrução while, à instrução controlada pela instrução dowhile chama-se passo e à condição que a controla guarda G. A execução da instrução de iteração do while pode ser representada pelo seguinte fluxograma:

Note-se que, ao contrário do que se passa com a instrução while, durante a execução de uma instrução dowhile o passo é executado sempre pelo menos uma vez.
for(int i = 0; i != 10; ++i)Se se pretender escrever no ecrã uma linha com 10 asteriscos, pode-se usar o seguinte código:
cout << i << endl;
for(int i = 0; i != 10; ++i)É importante observar que, em C++, é típico começar as contagens em zero (0) e usar como guarda o total de repetições a efectuar. Nos ciclos acima a variável i toma todos os valores entre 0 e 10 inclusivé, embora para i = 10 a acção do ciclo não chegue a ser executada. Alterando o primeiro ciclo de modo a que a definição da variável i seja feita fora do ciclo e o seu valor no final do ciclo mostrado no ecrã
cout << '*';
cout << endl; // para terminar a linha.
int i = 0;então a execução deste troço de código resultaria em
for(; i != 10; ++i)
cout << i << endl;
cout << "O valor final é " << i << endl;
0
1
2
3
4
5
6
7
8
9
O valor final é 10
cout << "Introduza valor (0 a 10): ";A instrução cin >> n aparece duas vezes, o que não parece uma solução muito elegante. Isto deve-se a que, antes de entrar no ciclo para a primeira iteração, tem de fazer sentido verificar se n está ou não dentro dos limites impostos, ou seja, a variável n tem de ter um valor que não seja arbitrário. A alternativa usando o ciclo do while seria:
cin >> n;
while(n < 0 || n > 10) {
cout << "Incorrecto, introduza de novo (0 a 10): ";
cin >> n;
}
cout << "Introduza valor (0 a 10): ";Este ciclo executa o corpo pelo menos uma vez dado que a guarda só é avaliada depois da primeira execução. Assim, só é necessária uma instrução cin >> n. A contrapartida é a necessidade da instrução alternativa if dentro do ciclo...
do {
cin >> n;
if(n < 0 || n > 10)
cout << "Incorrecto, introduza de novo (0 a 10): ";
} while(n < 0 || n > 10);
Em geral os ciclos while e for são suficientes para resolver os problemas, sendo muito raras as utilizações onde a utilização de do while resulta em código realmente mais claro.
| inic
while(G) { acção prog } |
é equivalente a | for(inic; G; prog)
acção |
| inic
while(G) passo |
é equivalente a | for(inic; G;)
passo |
| inic
while(G) passo |
é equivalente a | // Má ideia...
|
| do
passo while(G); |
é equivalente a | passo
while(G) passo |
Embora sejam válidas em geral, estas equivalências não são verdadeiras se as instruções controladas incluirem as instruções return, break, continue, ou goto (ver abaixo). Também há diferença quanto ao âmbito de variáveis definidas nestas instruções.
#include <iostream>Sugere-se que o leitor faça o traçado deste programa e/ou o execute em modo de depuração para compreender os dois ciclos encadeados.
using namespace std;// Escreve um triângulo oco de asteriscos com a altura passada como argumento:
// PC: altura >= 0
// CO: o ecrã contém altura linhas adicionais representando um
// triângulo rectângulo oco de asteriscos.
void escreveTriânguloOco(const int altura)
{
for(int i = 0; i != altura; ++i) {
for(int j = 0; j <= i; ++j)
if(j == 0 || j == i || i == altura - 1)
cout << '*';
else
cout << ' ';
cout << endl;
}
}int main()
{
cout << "Introduza a altura do triângulo: ";
int a;
cin >> a;escreveTriânguloOco(a);
}
// PC: n >= 0Este tipo de terminação abrupta de ciclos pode ser muito útil, mas também pode contribuir para tornar difícil a compreensão dos programas. Deve portanto ser usado com precaução e parcimónia e apenas em funções ou procedimentos muito curtos. Noutros casos torna-se preferível usar técnicas de reforço das guardas do ciclo (ver também Secção 4.4.4, Exemplo 1).
// CO: éPrimo = ((Qi : 2 <= i < n : n ÷ i <> 0) e n > 1)
bool éPrimo(const int n)
{
if(n <= 1)
return false;for(k = 2; k != n; ++k)
if(n % k == 0)
// Se se encontrou um divisor >= 2 e < n, então n não é primo
// e pode-se retornar imediatamente:
return false;
return true;
}
Outras possibilidades de alterar o funcionamento normal dos ciclos são através das instruções de break, continue, e goto.
A sintaxe da última encontra-se em qualquer livro sobre o C++ (e.g., [6]), e não será explicada aqui. Desaconselha-se vivamente a sua utilização.
A instrução break serve para terminar abruptamente a instrução while, for, do while, ou switch mais interior dentro da qual se encontre (ou seja, se existirem duas dessas instruções encadeadas, uma instrução de break termina apenas a instrução interior), continuando a execução na instrução subsequente.
A instrução continue é semelhante à instrução break, mas serve para começar antecipadamente a próxima iteração do ciclo (apenas no caso das instruções while, for e do while).
Às instruções break e continue aplicam-se as recomendações feitas quanto à utilização da instrução return dentro de ciclos: usar pouco e com cuidado.
cout << "Introduza valor (0 a 10): ";e
cin >> n;
while(n < 0 || n > 10) {
cout << "Incorrecto, introduza de novo (0 a 10): ";
cin >> n;
}
cout << "Introduza valor (0 a 10): ";Ambas deixam um amargo de boca. A primeira porque obriga à repetição da instrução de leitura do valor, que portanto aparece antes da instrução while e no seu passo. A segunda porque obriga a uma instrução alternativa cuja guarda é a negação da guarda do ciclo. O problema está em que teste da guarda deveria ser feito não antes do passo (como na instrução while), nem depois do passo (como na instrução do while), mas dentro do passo! Ou seja, negando a guarda da instrução de selecção e usando uma instrução break,
do {
cin >> n;
if(n < 0 || n > 10)
cout << "Incorrecto, introduza de novo (0 a 10): ";
} while(n < 0 || n > 10);
cout << "Introduza valor (0 a 10): ";que, como a guarda do ciclo é sempre verdadeira quando é verificada (quando n é válido o ciclo termina na instrução break, sem se testar a guarda), é equivalente a
do {
cin >> n;
if(n >= 0 || n <= 10)
break;
cout << "Incorrecto, introduza de novo (0 a 10): ";
} while(n < 0 || n > 10);
cout << "Introduza valor (0 a 10): ";que é mais comum escrever como
do {
cin >> n;
if(n >= 0 || n <= 10)
break;
cout << "Incorrecto, introduza de novo (0 a 10): ";
} while(true);
cout << "Introduza valor (0 a 10): ";Os ciclos do while(true), for(;;), e while(true) são ciclos infinitos ou laços, que só terminam com recurso a uma instrução break ou return *.
while(true) {
cin >> n;
if(n >= 0 || n <= 10)
break;
cout << "Incorrecto, introduza de novo (0 a 10): ";
}
* Noutras linguagens existe uma construção loop para este efeito, que pode ser simulada em C++ recorrendo ao pré-processador (ver capítulos posteriores):
#define loop while(true)loop {
cout << "Introduza valor (0 a 10): ";
cin >> n;
if(0 <= n && n <= 10)
break;
cout << "Incorrecto! ";
}
for(int i = 0; i <= 10; ++i)que escreve um asterisco a mais. É necessário ter muito cuidado com a guarda dos ciclos, pois estes erros são muito comuns e, por vezes, difíceis de detectar.
cout << '*';
Outro problema comum corresponde a colocar um ; após o cabeçalho de um ciclo. Por exemplo:
int i = 0;Neste caso o ciclo nunca termina, pois a instrução controlada pelo while (o seu passo) é a instrução nula, que não afecta o valor de i. Um caso pior ocorre quando se usa um ciclo for:
while(i != 10);
{
cout << '*';
++i;
}
for(int i = 0; i != 10; ++i);Este caso é mais grave porque o ciclo termina! Mas, ao contrário do que o programador pretendia, este pedaço de código escreve apenas um asterisco, e não 10!
cout << '*';
A escrita de asserções para problemas um pouco mais complicados que os vistos até aqui requer a utilização de quantificadores. Quantificadores são formas matemáticas abreviadas de escrever expressões que envolvem a repetição de uma dada operação. Exemplos são os quantificadores aritméticos somatório e produto, e os quantificadores lógicos universal ("qualquer que seja") e existencial ("existe pelo menos um").
Apresentam-se aqui algumas notas sobre os quantificadores que são mais úteis para a construção de asserções acerca do estado dos programas. A notação utilizada encontra-se resumida no Apêndice A.
Os quantificadores escrever-se-ão sempre da seguinte forma:
(X v : predicado(v) : expressão(v))onde
Por exemplo, é um facto conhecido que o somatório do primeiros n inteiros não negativos (S i : 0 <= i < n : i) tem valor n (n - 1) / 2 se n > 0. Que acontece se n <= 0? Neste caso é evidente que a variável muda i não pode tomar quaisquer valores, e portanto o resultado é a soma de zero (0) termos. A soma de zero termos é zero (0), por ser esse o elemento neutro da soma. Logo, (S i : 0 <= i < n : i) = 0 se n <= 0. Em geral, (S i : m <= i < n : expressão(i)) = 0 se n <= m.
Se se pretender desenvolver uma função que calcule a soma dos n primeiros números ímpares positivos (sendo n um parâmetro da função), pode-se começar por escrever o seu cabeçalho bem como a PC e a CO, como habitual:
// PC: n >= 0Note-se que, mais uma vez, se fez o parâmetro da função constante, de modo a deixar claro que a função não lhe altera o valor.
// CO: somaÍmpares = (S i : 0 <= i < n : 2 i + 1)
int somaÍmpares(const int n)
{
...
}
Por exemplo, a definição de factorial é n! = (P i : 1 <= i <= n : i ) se n >= 0.
O produto de zero termos é um (1), por ser esse o elemento neutro da multiplicação. Ou seja, (P i : m <= i < n : expressão(i)) = 1 se n <= m.
Se se pretender desenvolver uma função que calcule o factorial de n (sendo n um parâmetro da função), pode-se começar por escrever o seu cabeçalho bem como a PC e a CO:
// PC: n >= 0
// CO: factorial = n! = (P i : 1 <= i <= n : i)
int factorial(const int n)
{
...
}
A conjunção de zero termos tem valor V (verdadeiro), por ser esse o elemento neutro da conjunção. Ou seja, (Qi : m <= i < n : predicado(i)) = V se n <= m *.
Por exemplo, a definição da função (matemática!) primo(n), que tem valor V se n é primo e F no caso contrário, é:
primo(n) = (Q i : 2 <= i < n : n ÷ i <> 0), se n >= 2, eou seja,
primo(n) = F, se 0 <= n < 2,
primo(n) = ((Q i : 2 <= i < n : n ÷ i <> 0) e n >= 2) para n >= 0sendo ÷ a operação resto da divisão inteira (como o operador % em C++).
Se se pretender desenvolver uma função (agora em C++) que devolva o valor lógico verdadeiro quando n (sendo n um parâmetro da função) é um número primo, e falso no caso contrário, pode-se começar por escrever o seu cabeçalho bem como a PC e a CO:
// PC: n >= 0* Se não é claro para si que o quantificador universal corresponde a uma sequência de conjunções, pense no significado de escrever "todos os humanos têm cabeça". A tradução para linguagem (quase) matemática seria "qualquer que seja h pertencente ao conjunto dos humanos, h tem cabeça". Como o conjunto dos humanos é finito, pode-se escrever por extenso, listando todos os possíveis humanos: "o Yeltsin (aparenta) ter cabeça e o Sampaio tem cabeça e ...". Isto é, a conjunção de todas as afirmações.
// CO: éPrimo = ((Qi : 2 <= i < n : n ÷ i <> 0) e n >= 2)
bool éPrimo(const int n)
{
...
}
* A afirmação "todos os marcianos têm cabeça" é verdadeira, pois não existem marcianos. Esta propriedade é menos intuitiva que no caso dos quantificadores soma e produto, mas é importante.
A disjunção de zero termos tem valor F (falso), por ser esse o elemento neutro da disjunção. Ou seja, (Ei : m <= i < n : predicado(i)) = F se n <= m *.
Este quantificador está estreitamente relacionado com o quantificador universal. É sempre verdade que ¬(Q i : m <= i < n : predicado(i)) = (Ei : m <= i < n : ¬predicado(i)), ou seja, se não é verdade que para qualquer i o predicado predicado(i) é verdadeiro, então existe pelo menos um i para o qual o predicado predicado(i) é falso. Aplicado à definição de número primo acima, tem-se ¬primo(n) = ¬(Qi : 2 <= i < n : n ÷ i <> 0) = (Ei : 2 <= i < n : n ÷ i = 0), para n > 1. I.e., um número maior do que 1 não é primo se for divisível por algum inteiro maior do que 1 e menor que ele próprio.
Se se pretender desenvolver uma função que devolva o valor lógico verdadeiro quando existir um número primo entre m e n exclusivé (sendo m e n parâmetros da função, com m não negativo), e falso no caso contrário, pode-se começar por escrever o seu cabeçalho bem como a PC e a CO:
// PC: m >= 0* Se não é claro para si que o quantificador existencial corresponde a uma sequência de disjunções, pense no significado de escrever "existe pelo menos um humano com cabeça". A tradução para linguagem (quase) matemática seria "existe pelo menos um h pertencente ao conjunto dos humanos tal que h tem cabeça". Como o conjunto dos humanos é finito, pode-se escrever por extenso, listando todos os possíveis humanos: "o Yeltsin tem cabeça ou o Sampaio tem cabeça ou ...". Isto é, a disjunção de todas as afirmações.
// CO: existePrimoNoIntervalo = (E i : m <= i < n : primo(i))
bool existePrimoNoIntervalo(const int m, const int n)
{
...
}
* A afirmação "existe pelo menos um marciano com cabeça" é falsa, pois não existem marcianos.
Este quantificador é extremamente útil quando é necessário especificar condições em que o número de ordem é fundamental. Se se pretender desenvolver uma função que devolva o n-ésimo número primo (sendo n parâmetro da função), pode-se começar por escrever o seu cabeçalho bem como a PC e a CO:
// PC: n >= 1ou seja, o valor devolvido é um primo e existem n - 1 primos de valor inferior.
// CO: primo(primo) e (N i : 0 <= i < primo : primo(i)) = n - 1
int primo(const int n)
{
...
}
* A definição de resto pode ser generalizada para englobar valores negativos de m e n. Em qualquer dos casos tem de existir um quociente q tal que m = q × n + r. Mas o intervalo onde r se encontra varia:
0 <= r < n se m >= 0 e n > 0 (neste caso q >= 0)
0 <= r < -n se m >= 0 e n < 0 (neste caso q <= 0)
-n < r <= 0 se m <= 0 e n > 0 (neste caso q <= 0)
n < r <= 0 se m <= 0 e n < 0 (neste caso q >= 0)
Suponha-se que se pretende desenvolver uma função para calcular a potência n de x, isto é, uma função que, sendo x e n os seus dois parâmetros, devolva xn. A sua estrutura básica é portanto:
double potência(double x, int n)É claro que xn = x × x ... × x, ou seja, xn pode ser obtido por multiplicação repetida de x. Assim, uma solução é usar um ciclo que no seu passo faça cada uma dessas multiplicações:
{
...
}
double potência(double x, int n)Será que o ciclo está correcto? Fazendo um traçado da função admitindo que é chamada com os argumentos 5,0 e 2, verifica-se facilmente que devolve 125,0 e não 25,0! Isso significa que é feita uma multplicação a mais. Observando com atenção a guarda da instrução de iteração, conclui-se que esta não deveria deixar o contador i atingir o valor de n. Ou seja, a guarda deveria ser i < n e não i <= n. Corrigindo a função:
{
int i = 1; // usada para contar o número de x já incluidos no produto.
double r = x; // usada para acumular os produtos de x.
while(i <= n) {
r *= x; // o mesmo que r = r * x;
++i; // o mesmo que i = i + 1;
}
return r;
}
double potência(double x, int n)Estará o ciclo definitivamente correcto? Fazendo traçados da função admitindo que é chamada com argumentos 5,0 e 2 e com 5,0 e 3, facilmente se verifica que devolve respectivamente 25,0 e 125,0, pelo que aparenta estar correcta. Mas estará correcta para todos os valores? E se os argumentos forem 5,0 e 0? Nesse caso a função devolve 5,0 em vez do valor correcto, que é 5,00 = 1,0! Observando com atenção a inicialização do contador e do acumulador dos produtos, conclui-se que estes deveriam ser inicializados com 0 e 1,0, respectivamente. Corrigindo a função:
{
int i = 1; // usada para contar o número de x já incluidos no produto.
double r = x; // usada para acumular os produtos de x.
while(i < n) {
r *= x; // o mesmo que r = r * x;
++i; // o mesmo que i = i + 1;
}
return r;
}
double potência(double x, int n)Neste momento a função parece estar correcta. Mas que acontece se o expoente for negativo? Fazendo o traçado da função admitindo que é chamada com os argumentos 5,0 e -1, facilmente se verifica que devolve 1,0 em vez de 5,0-1 = 0,2!
{
int i = 0; // usada para contar o número de x já incluidos no produto.
double r = 1.0; // usada para acumular os produtos de x.
while(i < n) {
r *= x; // o mesmo que r = r * x;
++i; // o mesmo que i = i + 1;
}
return r;
}
Os vários problemas que surgiram ao longo desde desenvolvimento atribulado deveram-se a que:
// PC: n >= 0É importante verificar agora o que acontece se o programador utilizador da função se enganar e, violando o contrato expresso pela PC e pela CO, a invocar com um expoente negativo. Como se viu, a função simplesmente devolve um valor errado: 1,0. Isso acontece porque, sendo n negativo e i inicializado com 0, a guarda é inicialmente falsa, não sendo o passo do ciclo executado nenhuma vez. É possível enfraquecer a guarda, de modo a que seja falsa em menos circunstâncias, e de tal forma que o contrato da função se mantenha: basta substituir i < n por i != n. É óbvio que para valores do expoente não-negativos as duas guardas são equivalentes. Mas para expoentes negativos a nova guarda leva a um ciclo infinito! O contador i vai crescendo a partir de zero, afastando-se irremediavelmente do valor negativo de n.
// CO: potência = xn
double potência(const double x, const int n)
{
int i = 0; // usada para contar o número de x já incluidos no produto.
double r = 1.0; // usada para acumular os produtos de x.
while(i < n) {
r *= x; // o mesmo que r = r * x;
++i; // o mesmo que i = i + 1;
}
return r;
}
Qual das guardas será preferível? A primeira, que em caso de engano por parte do programador utilizador da função devolve um valor errado, ou a segunda, que nesse caso entra num ciclo infinito, não chegando a terminar? A verdade é que é preferível a segunda, pois o programador utilizador mais facilmente se apercebe do erro e o corrige em tempo útil *. Com a segunda guarda o problema pode só ser detectado demasiado tarde. Assim, a nova versão da função será:
// PC: n >= 0Isto resolve o primeiro problema. E o segundo?
// CO: potência = xn
double potência(const double x, const int n)
{
int i = 0; // usada para contar o número de x já incluidos no produto.
double r = 1.0; // usada para acumular os produtos de x.
while(i != n) {
r *= x; // o mesmo que r = r * x;
++i; // o mesmo que i = i + 1;
}
return r;
}
É possível certamente desenvolver código C++ "ao sabor da pena", mas é importante que seja desenvolvido correctamente. Significa isto que, para ciclos mais simples ou conhecidos, o programador desenvolve-os rapidamente, sem grandes preocupações. Mas para ciclos mais complicados o programador deve ter especial atenção à sua correcção. Das duas uma, ou os desenvolve primeiro e depois demonstra a sua correcção, ou usa uma metodologia de desenvolvimento que garanta a sua correcção. As próximas secções lidam com estes dois problemas: o da demonstração de correcção de ciclos e o de metodologias de desenvolvimento de ciclos. Antes, porém, é fundamental apresentar a noção de invariante um ciclo.
Em alguns casos, porém, a utilização desta metodologia não é prática, uma vez que requer um arsenal considerável de modelos: é o caso de ciclos que envolvam leituras do teclado e/ou escritas no ecrã. Nesses casos a metodologia continua aplicável, como é óbvio, embora seja vulgar que as asserções sejam escritas com muito menos formalismo.
* Note-se que na realidade o ciclo não é infinito, pois os int são limitados e incrementações sucessivas levarão o valor do contador ao limite superior dos int. O que acontece depois depende do compilador, sistema operativo e máquina em que o programa foi compilado e executado. Normalmente o que acontece é que uma incrementação feita ao contador quando o seu valor já atingiu o limite superior dos int leva o valor a "dar a volta" aos inteiros, passando para o limite inferior dos int. Incrementações posteriores levarão o contador até zero, pelo que em rigor o ciclo não é infinito... Mas demora muito tempo a executar, pelo menos, o que mantém a validade do argumento usado para justificar a fraqueza das guardas.
// PC: n >= 0Suponha-se que a função é invocada com os argumentos 3,0 e 4. Isto é, suponha-se que quando a função começa a ser executada as constantes x e n têm os valores 3,0 e 4. Faça-se um traçado da execução da função anotando o valor das suas variáveis em cada um dos pontos entre instruções assinalados. Obtém-se a seguinte tabela:
// CO: potência = xn
double potência(const double x, const int n)
{
int i = 0; // usada para contar o número de x já incluidos no produto.
double r = 1.0; // usada para acumular os produtos de x.
ponto 1, depois da inicialização do ciclo, i.e., depois da inicialização das variáveis nele envolvidas.
while(i != n) {
ponto 2, depois de se verificar que a guarda é verdadeira.
r *= x; // o mesmo que r = r * x;
ponto 3, depois de acumular mais uma multiplicação de x em r.
++i; // o mesmo que i = i + 1;
ponto 4, depois de incrementar o contador do número de x já incluidos no produto r.
}
ponto 5, depois de se verificar que a guarda é falsa, imediatamente antes do retorno.
return r;
}
|
|
|
|
comentários |
|---|---|---|---|
|
|
|
|
como 0 <> 4, o passo do ciclo será executado, passando-se ao ponto 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
como 1 <> 4, o passo do ciclo será executado, passando-se ao ponto 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
como 2 <> 4, o passo do ciclo será executado, passando-se ao ponto 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
como 3 <> 4, o passo do ciclo será executado, passando-se ao ponto 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
como 4 <> 4 é falso, o ciclo termina, passando-se ao ponto 5 |
|
|
|
|
É fácil verificar que há uma condição relacionando x, r, n e i que se verifica em todos os pontos do ciclo com excepção do ponto 3. I.e., que se verifica depois da inicialização, antes do passo, depois do passo, e no final do ciclo. A relação é r = xi e 0 <= i <= n. Esta relação diz algo razoavelmente óbvio: em cada instante (excepto no ponto 3) o acumulador possui a potência i do valor em x, tendo i um valor entre 0 e n. Esta condição, por ser verdadeira ao longo de todo o ciclo (excepto a meio do passo, no ponto 3), diz-se uma "invariante" do ciclo.
As condições invariantes são centrais na demonstração da correcção de ciclos e durante o desenvolvimento disciplinado de ciclos, como se verá nas próximas secções.
Em geral, para um ciclo da forma
inicuma condição diz-se invariante (CI) se
while(G)
passo
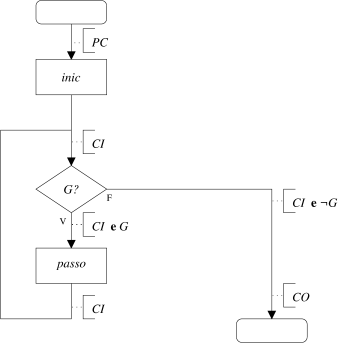
Note-se que se incluiram asserções adicionais. Antes da inicialização assume-se que a pré-condição (PC) do ciclo se verifica, e no final do ciclo pretende-se que se verifique a sua condição objectivo (CO). Além disso, depois da decisão do ciclo, em que se verifica a veracidade da guarda, sabe-se que a guarda (G) é verdadeira antes de executar o passo e falsa (ou seja, verdadeira a sua negação ¬G) depois de terminado o ciclo. Ou seja, antes do passo sabe-se que CI e G é uma asserção verdadeira e no final do ciclo sabe-se que CI e ¬G é também uma asserção verdadeira.
Note-se que, no caso da função potência(), a condição objectivo do ciclo é diferente da condição objectivo da função, pois refere-se à variável r, que será posteriormente devolvida pela função. I.e.:
// PC: n >= 0
// CO: potência = xn
double potência(const double x, const int n)
{
// PC: n >= 0
int i = 0; // usada para contar o número de x já incluidos no produto.
double r = 1.0; // usada para acumular os produtos de x.
while(i != n) {
r *= x; // o mesmo que r = r * x;
++i; // o mesmo que i = i + 1;
}
// CO': r = xn
return r;
}
Para que a asserção CI possa ser invariante tem de ser verdadeira depois da inicialização (ver fluxograma). I.e., assumindo que a PC do ciclo se verifica, então a inicialização inic tem de conduzir forçosamente à veracidade da asserção CI. É necessário portanto demonstrar que:
// PCPara o exemplo do cálculo da potência isso é uma tarefa simples. Nesse caso tem-se:
inic
// implica CI
// PC: n >= 0A demonstração neste pode ser feita substituindo na CI os valores iniciais de r e i:
int i = 0;
double r = 1.0;
// CI: r = xie 0 <= i <= n
CI: 1,0 = x0 e 0 <= 0 <= n, ou sejaNeste momento demonstrou-se a veracidade da asserção CI depois da inicialização. Falta demonstrar que é verdadeira antes do passo, depois do passo, e no fim do ciclo. A demonstração pode ser feita por indução. Supõe-se que a asserção CI é verdadeira antes do passo numa qualquer iteração do ciclo e demonstra-se que é também verdadeira depois do passo nessa mesma iteração. I.e., como antes do passo a guarda é forçosamente verdadeira, pois de outra forma o ciclo teria terminado, é necessário demonstrar que:
CI: 1,0 = 1,0 e 0 <= 0 e 0 <= n, ou seja
CI: V e V e 0 <= n, ou seja
CI: 0 <= n, que é garantidamente verdadeira dada a PC, ou seja
CI: V
// CI e GSe esta demonstração for possível, então por indução a asserção CI será verdadeira ao longo de todo o ciclo, i.e., antes e depois do passo em qualquer iteração do ciclo e no final do ciclo. Isso pode ser visto claramente observando o fluxograma. Como se demonstrou que a asserção CI é verdadeira depois da inicialização, então também será verdadeira depois de verificada a guarda pela primeira vez, visto que a verificação da guarda não altera qualquer variável do programa. Ou seja, se a guarda for verdadeira a asserção CI será verdadeira antes do passo na primeira iteração do ciclo e, se a guarda for falsa, a asserção CI será verdadeira no final do ciclo. Se a guarda for verdadeira, como se demonstrou que a veracidade de CI antes do passo numa qualquer iteração implica a sua veracidade depois do passo na mesma iteração, conclui-se que, quando se for verificar de novo a guarda do ciclo (ver fluxograma) a asserção CI é verdadeira. Logo, pode-se repetir o argumento para a segunda iteração do ciclo e assim sucessivamente.
passo
// implica CI
Para o caso dado, é necessário demonstrar que:
// CI e G: r = xi e 0 <= i <= n ei <> n, ou seja, simplificandoA demonstração pode ser feita verificando qual a pré-condição mais fraca de cada uma das atribuições, do fim para o princípio (ver Dedução da pré-condição mais fraca de uma atribuição). Obtém-se:
// r = xi e 0 <= i < n
r *= x; // o mesmo que r = r * x;
++i; // o mesmo que i = i + 1;
// CI: r = xie 0 <= i <= n
// r = xi+1e 0 <= i + 1 <= n, ou sejaou seja, para que a asserção CI se verifique depois da incrementação de i é necessário que se verifique a asserção
// r = xi × xe -1 <= i <= n - 1, ou seja
// r = xi × xe -1 <= i < n
++i; // o mesmo que i = i + 1;
// CI: r = xie 0 <= i <= n
r = xi × x e -1 <= i < nantes da incrementação. Aplicando a mesma técnica à atribuição anterior tem-se que:
// r × x = xi × x e -1 <= i < n, ou seja, eliminando x de ambos os lados da igualdade,Falta portanto demonstrar que
// r = xi e -1 <= i < n
r *= x; // o mesmo que r = r * x;
// r = xi × xe -1 <= i < n
CI e G: r = xie 0 <= i < nmas isso verifica-se por mera observação (se i >= 0, então forçosamente i >= - 1).
implica r = xi e -1 <= i < n
Em resumo, para provar a invariância de uma asserção CI é necessário:
CI e ¬G: r = xie 0 <= i <= n e i = n é o mesmo queEm resumo, para provar a correcção parcial de um ciclo é necessário:
r = xi e i = n , ou seja
r = xn e i = n , que implica naturalmente
CO': r = xn
// PC: n >= 0É fácil demonstrar a correcção parcial deste ciclo (porquê?)! Mas este ciclo não termina nunca excepto quando n é 0. I.e., de acordo com a definição dada na Secção 1.3, este ciclo não implementa um algoritmo, pois não verifica a propriedade da finitude.
// CO: potência = xn
double potência(const double x, const int n)
{
// PC: n >= 0
int i = 0;
double r = 1.0;
while(i != n)
; // instrução vazia!
// CO': r = xn
return r;
}
A demonstração formal de terminação de um ciclo ao fim de um número finito de iterações faz-se usando o conceito de "função de limitação" (bound functions) [4], que não será abordado neste texto. Neste contexto será suficiente a demonstração informal desse facto. Por exemplo, na versão original da função potência()
// PC: n >= 0é evidente que, como a variável i começa com o valor zero e é incrementada de uma unidade ao fim de cada passo, fatalmente tem de atingir o valor de n (que, pela PC, é não-negativo). Em particular é fácil verificar que o número exacto de iterações necessário para isso acontecer é exactamente n.
// CO: potência = xn
double potência(const double x, const int n)
{
// PC: n >= 0
int i = 0; // usada para contar o número de x já incluidos no produto.
double r = 1.0; // usada para acumular os produtos de x.
while(i != n) {
r *= x; // o mesmo que r = r * x;
++i; // o mesmo que i = i + 1;
}
// CO': r = xn
return r;
}
O passo é, tipicamente, dividido em duas partes: a acção e o progresso. I.e., os ciclos têm tipicamente a seguinte forma:
iniconde o progresso prog corresponde ao conjunto de instruções que garante a terminação do ciclo e a acção acção corresponde ao conjunto de instruções que garante a invariância de CI apesar do progresso.
while(G) {
acção
prog
}
No caso do ciclo da função potência() a acção e o progresso são:
r *= x; // acção
++i; // prog
// PCé necessário:
inic
while(G) {
acção
prog
}
// CO
// PC: n >= 0 oux <> 0É fácil verificar que a resolução do problema exige o tratamento de dois casos distintos, resoluveis através de uma instrução de selecção, ou, mais simplesmente, através do operador ?::
// CO: potência = xn
double potência(const double x, const int n)
{
...
}
// PC: n >= 0 oux <> 0ou ainda, convertendo para a instrução de iteração for e eliminando os comentários redundantes
// CO: potência = xn
double potência(const double x, const int n)
{
const int exp = n < 0 ? -n : n;
int i = 0; // usada para contar o número de x já incluidos no produto.
double r = 1.0; // usada para acumular os produtos de x.
while(i != exp) {
r *= x; // o mesmo que r = r * x;
++i; // o mesmo que i = i + 1;
}
return n < 0 ? 1.0 / r : r;
}
// PC: n >= 0 oux <> 0
// CO: potência = xn
double potência(const double x, const int n)
{
const int exp = n < 0 ? -n : n;
double r = 1.0;
for(int i = 0; i != exp; ++i)
r *= x; // o mesmo que r = r * x;
return n < 0 ? 1.0 / r : r;
}
A definição destas condições, no caso de uma função ou procedimento, funciona como um contrato com o programador utilizador da função ou procedimento: "se o programador utilizador desta função (procedimento) respeitar a PC, o programador fabricante desta função (procedimento) garante que depois de executada(o) a CO é verdadeira".
Se se pretender escrever uma função int somaQuadrados(const int n) que some os quadrados dos primeiros n inteiros não-negativos, então a estrutura da função, com a PC e a CO, poderá ser:
// PC: n >= 0onde CO' é a condição objectivo do corpo da função antes da instrução de retorno.
// CO: somaQuadrados = (S k : 0 <= k < n : k2)
int somaQuadrados(const int n)
{
int resultado = ???;// CO': somaQuadrados = (S k : 0 <= k < n : k2)
return resultado;
}
Se se pretender escrever uma função int raiz(const int x) que, assumindo que x é não-negativo, devolva o maior inteiro menor ou igual à raiz quadrada de x, então a estrutura da função, com a PC e a CO, poderá ser:
// PC: x >= 0onde CO' é a condição objectivo do corpo da função antes da instrução de retorno. Esta função, no fundo, devolve uma aproximação da raiz quadrada de um inteiro. Note-se que é a relação x < (r + 1)2 que garante que o valor devolvido é o maior inteiro menor ou igual a x½.
// CO: 0 <= raizInteira <= x½ < raizInteira + 1, ou seja,
// 0 <= raizInteiraeraizInteira2 <= x < (raizInteira + 1)2
int raizInteira(const int x)
{
int r = ???;// CO': 0 <=r e r2 <= x < (r + 1)2
return r;
}
Por enfraquecimento entende-se a obtenção de uma condição invariante CI tal que, de entre todas as combinações de valores das variáveis que a tornam verdadeira, contenha todas as combinações de valores de variáveis que tornam verdadeira a CO. Ou seja, o conjunto dos estados do programa que verificam a CI deve conter o conjunto dos estados do programa que verificam a CO. Ou ainda, CO implica CI.
Apresentar-se-ão aqui apenas dois dos vários possíveis métodos para obter a CI por enfraquecimento da CO:
Voltando à função somaQuadrados(), é evidente que o corpo da função pode consistir num ciclo cuja condição objectivo já foi apresentada:
CO': resultado = (S k: 0 <= k < n : k2).A CI do ciclo pode ser obtida substituindo na CO' a constante n por uma nova variável C++ i, com limites apropriados, ficando portanto:
CI: resultado = (S k: 0 <= k < i : k2) e 0 <= i <= n.Note-se que só se pode confirmar se a escolha da CI foi apropriada depois de completado o desenvolvimento do ciclo. Se o não for, há que voltar a este passo e tentar de novo.
Em rigor, a escolha feita para CI não corresponde ao simples enfraquecimento da CO'. Na verdade, a introdução de uma nova variável é feita em duas etapas, que normalmente se omitem. O primeiro passo obriga a uma reformulação da CO' de modo a reflectir a existência da nova variável. Substitui-se a constante pela nova variável, mas força-se também a nova variável a tomar o valor da constante que substituiu, acrescentando para tal uma conjunção à CO'
CO'': resultado = (S k: 0 <= k < i : k2) ei = n,de modo a garantir que CO'' implica CO'.
A CI é obtida da nova CO'' por enfraquecimento do termo que fixa o valor da variável i, que na CI é deixada mais "livre" que na CO''. A CI obtida é de facto mais fraca que a CO'', pois aceita mais possíveis valores para a variável resultado do que a CO'', que só aceita o resultado final pretendido. Os valores aceites para essa variável pela CI correspondem a valores intermédios durante o cálculo. Neste caso correspondem a todas as possíveis somas de quadrados de inteiros positivos: desde a soma com zero termos até à soma com os n termos pretendidos.
A escolha da guarda também é simples. Basta escolher para negação da guarda ¬G a conjunção que se acrescentou à CO' para se obter a CO''. Dessa forma tem-se forçosamente que (CI e ¬G)equivaleCO''implica CO', como pretendido.
A escolha da G pode também ser feita observando que no final do ciclo a guarda será forçosamente falsa e a CI verdadeira (i.e., que CI e ¬G), e que pretende, nessa altura, que a CO' do ciclo seja verdadeira. Ou seja, sabe-se que no final do ciclo
resultado = (S k: 0 <= k < i: k2) e 0 <= i <= n e ¬Ge pretende-se que
CO': resultado = (S k: 0 <= k < n : k2).A escolha mais simples da guarda que garante a verificação da CO' é
¬G: i = n,
ou seja,
G: i <> n
Voltando à função raiz(), é evidente que o corpo da função pode consistir num ciclo cuja condição objectivo já foi apresentada:
CO': 0 <= rer2 <= x < (r + 1)2,ou seja,
CO': 0 <= rer2 <= xe x < (r + 1)2.Escolhendo para negação da guarda ¬G o predicado x < (r + 1)2, ou seja, escolhendo
G: (r + 1)2 <= x,obtém-se
CI: 0 <= rer2 <= x.Esta escolha faz com que CI e ¬G seja equivalente a CO', pelo que, se o ciclo terminar, termina com o valor correcto.
Esta escolha de CI corresponde, mais uma vez, a enfraquecer a CO', pois a CI aceita mais possíveis valores para a variável r do que a CO', que só aceita o resultado final pretendido.
CI: resultado = (S k: 0 <= k < i : k2) e 0 <= i <= n,pelo que a forma mais simples de se inicializar o ciclo é com as instruções
int resultado = 0;pois nesse caso a CI fica
int i = 0;
0 = (S k: 0 <= k < 0 : k2) e 0 <= 0 <= n,que tem sempre valor V, pois a PC indica que n >= 0.
CI: 0 <= rer2 <= x,pelo que a forma mais simples de se inicializar o ciclo é com a instrução
int r = 0;pois nesse caso a CI fica
0 <= 0 e 0 <= x,que tem sempre valor V, pois a PC indica que x >= 0.
G: i <> npelo que o progresso mais simples é a simples incrementação de i. Este progresso garante que o ciclo termina ao fim de no máximo n iterações. Ou seja, o passo do ciclo é
// CI eG: resultado = (S k : 0 <= k < i : k2) e 0 <= i <= ne i <> n,onde se assume a CI como verdadeira antes da acção e se pretende escolher uma acção de modo a que o seja também depois do passo, ou melhor, apesar do passo. Usando a semântica da operação de atribuição, pode-se deduzir a condição mais fraca antes do progresso de modo a que CI seja verdadeira no final do passo:
// ou seja,
// resultado = (Sk : 0 <= k < i : k2) e 0 <= i < n
acção
++i; // i = i + 1;
// CI: resultado = (S k : 0 <= k < i : k2) e 0 <= i <= n
// resultado = (S k : 0 <= k < i + 1 : k2) e 0 <= i + 1 <= n,Falta determinar uma acção tal que
// ou seja, extraíndo o último termo do somatório,
// resultado = (Sk : 0 <= k < i : k2) + i2e -1 <= i < n,
++i; // i = i + 1;
// CI: resultado = (S k : 0 <= k < i : k2) e 0 <= i <= n
// resultado = (S k : 0 <= k < i : k2) e 0 <= i < nA acção mais simples é portanto:
acção
// resultado = (Sk : 0 <= k < i : k2) + i2e -1 <= i < n
resultado += i * i;pelo que o o ciclo (e a função) completo é
// PC: n >= 0ou, substituindo pelo ciclo com a instrução for equivalente:
// CO: somaQuadrados = (S k : 0 <= k < n : k2)
int somaQuadrados(const int n)
{
int resultado = 0;
int i = 0;// CI: resultado = (S k : 0 <= k < i : k2) e 0 <= i <= n
while(i != n) {
resultado += i * i;
++i;
}return resultado;
}
// PC: n >= 0
// CO: somaQuadrados = (S k : 0 <= k < n : k2)
int somaQuadrados(const int n)
{
int resultado = 0;// CI: resultado = (S k : 0 <= k < i : k2) e 0 <= i <= n
for(int i = 0; i != n; ++i)
resultado += i * i;return resultado;
}
G: (r + 1)2 <= x,pelo que o progresso mais simples é a simples incrementação de r, que levará forçosamente à falsidade da guarda. Ou seja, o passo do ciclo é
// CI eG: 0 <= r e r2 <= xe (r + 1)2 <= x,onde se assume a CI como verdadeira no antes da acção e se pretende escolher uma acção de modo a que o seja também depois do passo. Usando a semântica da operação de atribuição, pode-se deduzir a condição mais fraca antes do progresso de modo a que CI seja verdadeira no final do passo:
acção
++r; // r = r + 1;
// CI: 0 <= rer2 <= x
// CI eG: 0 <= r e r2 <= xe (r + 1)2 <= x,Como 0 <= r implica -1 <= r, então é evidente que neste caso não é necessária qualquer acção! Assim, o ciclo (a função) completo é:
acção
// 0 <= r + 1 e (r + 1)2 <= x, ou seja,
// -1 <= re (r + 1)2 <= x
++r; // r = r + 1;
// CI: 0 <= rer2 <= x
// PC: x >= 0A guarda do ciclo pode ser simplificada se se adiantar a variável r de uma unidade. Ou seja:
// CO: 0 <= raizInteira <= x½ < raizInteira + 1
int raizInteira(const int x)
{
int r = 0;// CI: 0 <= r e r2 <= x
while((r + 1) * (r + 1) <= x)
++r;return r;
}
// PC: x >= 0
// CO: 0 <= raizInteira <= x½ < raizInteira + 1
int raizInteira(const int x)
{
int r = 1;// CI: 1 <= r e (r - 1)2 <= x
while(r * r <= x)
++r;return r - 1;
}
// PC: n >= 0
// CO: somaQuadrados = (S k : 0 <= k < n : k2)
int somaQuadrados(const int n)
{
return n * (n - 1) / 2 * (2 * n - 1) / 3;
}
O primeiro passo é a escrita da estrutura da função, incluindo as respectivas PC e CO (ver Secção 4.4.4):
// PC: n >= 0Como abordar este problema? Em primeiro lugar, é conveniente verificar que os valores 0 e 1 são casos particulares. O primeiro porque é divisível por todos os inteiros positivos e portanto não pode ser primo. O segundo porque, apesar de só ser divisível por 1 e por si próprio, não é considerado, por convenção, um número primo. Estes casos particulares podem ser tratados com recurso a uma simples instrução condicional, pelo que se pode reescrever a função como
// CO: éPrimo = ((Qj : 2 <= j < n : n ÷ j <> 0) e n >= 2)
bool éPrimo(const int n)
{
...
}
// PC: n >= 0uma vez que, se a guarda da instrução condicional for falsa, e sabendo que n >= 0 pela PC, então forçosamente n >= 2 depois da instrução condicional.
// CO: éPrimo = ((Q j : 2 <= j < n : n ÷ j <> 0) e n >= 2)
bool éPrimo(const int n)
{
if(n == 0 || n == 1)
return false;// PC': n >= 2
bool é_primo;
...
// CO': é_primo = (Q j : 2 <= j < n : n ÷ j <> 0)
return é_primo;
}
Assim, o problema resume-se a escrever o código que leve de PC' e CO'. Um ciclo parece ser apropriado para resolver este problema, pois para verificar se um número n é primo pode-se ir verificando se é divisível por algum inteiro entre 2 e n - 1.
A condição invariante do ciclo pode ser obtida substituindo o limite superior da conjunção (a constante n) por uma variável i criada para o efeito. Assim, obtém-se a seguinte estrutura para o ciclo
// PC': n >= 2O que significa esta condição invariante? Simplesmente que a variável é_primo tem valor lógico verdadeiro se e só se não existirem divisores de n superiores a 1 e inferiores a i, sendo i um valor entre 2 e n. Ou melhor, significa que, num dado passo do ciclo, já se testaram todos os potenciais divisores de n entre 2 e i exclusivé.
int i;
bool é_primo;
inic
// CI: (é_primo = (Q j : 2 <= j < i : n ÷ j <> 0)) e 2 <= i <= n
while(G)
passo
// CO': é_primo = (Q j : 2 <= j < n : n ÷ j <> 0)
A escolha da guarda é muito simples: quando o ciclo terminar CI e ¬G deve implicar a CO. Isso consegue-se simplesmente fazendo ¬G: i = n, ou seja, G: k <> n. Quanto à inicialização, também é simples, pois basta atribuir 2 a i para que a conjunção não tenha qualquer termo e portanto tenha valor lógico V. Assim, a inicialização é:
int i = 2;Ou seja
bool é_primo = true;
// PC': n >= 2Que progresso utilizar? A forma mais simples de garantir a terminação do ciclo é simplesmente incrementar i. Dessa forma, como i começa com valor 2 e n >= 2 pela pré-condição, a guarda torna-se falsa, e o ciclo termina, ao fim de exactamente n - 2 iterações do ciclo. Ou seja
int i = 2;
bool é_primo = true;
// CI: (é_primo = (Q j : 2 <= j < i : n ÷ j <> 0)) e 2 <= i <= n
while(i != n)
passo
// CO': é_primo = (Q j : 2 <= j < n : n ÷ j <> 0)
// PC': n >= 2Finalmente, falta determinar a acção a executar para garantir a veracidade da CI apesar do progresso. No início do passo admite-se que a CI é verdadeira e sabe-se que a G é verdadeira, ou seja:
int i = 2;
bool é_primo = true;
// CI: (é_primo = (Q j : 2 <= j < i : n ÷ j <> 0)) e 2 <= i <= n
while(i != n) {
acção
++i;
}
// CO': é_primo = (Q j : 2 <= j < n : n ÷ j <> 0)
CI e G: (é_primo = (Q j : 2 <= j < i : n ÷ j <> 0)) e 2 <= i <= n ei <> nou seja,
(é_primo = (Q j : 2 <= j < i : n ÷ j <> 0)) e 2 <= i < nPor outro lado, no final do passo deseja-se que a CI seja verdadeira. Logo, o passo com as respectivas asserções é:
// Aqui admite-se que CI eG: (é_primo = (Q j : 2 <= j < i : n ÷ j <> 0)) e 2 <= i < nAntes de determinar a acção, é conveniente verificar qual a pré-condição mais fraca do progresso que é necessário impor para que, depois dele, se verifique a CI do ciclo. Usando a transformação de variáveis correspondente à atribuição i = i + 1 (equivalente a ++i), chega-se a:
acção
++i;
// Aqui pretende-se que: (é_primo = (Q j : 2 <= j < i : n ÷ j <> 0)) e 2 <= i <= n
// Aqui admite-se que CI eG: (é_primo = (Q j : 2 <= j < i : n ÷ j <> 0)) e 2 <= i < nAssim sendo, a acção deve ser tal que:
acção
// (é_primo = (Q j : 2 <= j < i + 1 : n ÷ j <> 0)) e 2 <= i + 1 <= n, ou seja,
// (é_primo = (Q j : 2 <= j < i : n ÷ j <> 0) e n ÷ i <> 0) e 1 <= i <= n - 1, ou seja,
// (é_primo = (Q j : 2 <= j < i : n ÷ j <> 0) e n ÷ i <> 0) e 1 <= i < n.
++i;
// Aqui pretende-se que: (é_primo = (Q j : 2 <= j < i : n ÷ j <> 0)) e 2 <= i <= n
// (é_primo = (Qj : 2 <= j < i : n ÷ j <> 0)) e 2 <= i < nÉ evidente, então, que a acção pode ser simplesmente:
acção
// implica (é_primo = (Q j : 2 <= j < i : n ÷ j <> 0) e n ÷ i <> 0) e 1 <= i < n.
é_primo = (é_primo && n % i != 0);onde os parênteses são dispensáveis dadas as regras de precedência dos operadores em C++ (Secção 2.5.6, Tabela Precedência de operadores).
A correcção da acção determinada pode ser verificada facilmente calculando a respectiva pré-condição mais fraca:
// (é_primo en ÷ i <> 0 = (Q j : 2 <= j < i : n ÷ j <> 0) e n ÷ i <> 0) e 1 <= i < n, ou seja,e observando que CI e G leva forçosamente à sua verificação:
// (é_primo = (Q j : 2 <= j < i : n ÷ j <> 0)) e 1 <= i < n.
é_primo = é_primo && n % i != 0;
// implica (é_primo = (Q j : 2 <= j < i : n ÷ j <> 0) e n ÷ i <> 0) e 1 <= i < n.
CI e G: (é_primo = (Qj : 2 <= j < i : n ÷ j <> 0)) e 2 <= i < nEscrevendo agora o ciclo completo tem-se:
implica (é_primo = (Q j : 2 <= j < i : n ÷ j <> 0)) e 1 <= i < n
// PC': n >= 2
int i = 2;
bool é_primo = true;
// CI: (é_primo = (Q j : 2 <= j < i : n ÷ j <> 0)) e 2 <= i <= n
while(i != n) {
é_primo = é_primo && n % i != 0;
++i;
}
// CO': é_primo = (Q j : 2 <= j < n : n ÷ j <> 0)
Em primeiro lugar é necessário demonstrar que, quando o ciclo termina, se atinge a CO'. Ou seja, será que CI e ¬G implica CO'? Neste caso
CI e ¬G: (é_primo = (Q j : 2 <= j < i : n ÷ j <> 0)) e 2 <= i <= n e (¬é_primo ou i = n)Considere-se o último termo da conjunção, ou seja, a disjunção (¬é_primo ou i = n). Quando o ciclo termina pelo menos um dos termos da disjunção é verdadeiro.
Suponha-se que ¬é_primo é V. Então ¬(Q j : 2 <= j < i : n ÷ j <> 0) é verdadeira, ou seja, (E j : 2 <= j < i : n ÷ j = 0) é verdadeira, pelo que (E j : 2 <= j < n : n ÷ j = 0) também o é (simplesmente se acrescentaram termos à disjunção) e portanto (Q j : 2 <= j < n : n ÷ j <> 0) é falsa. Ou seja, CO': é_primo = (Q j : 2 <= j < n : n ÷ j <> 0) é verdadeira (representa a tautologia F = F)!
Suponha-se que i = n. Este caso é idêntico ao caso sem reforço da guarda.
Logo, a CO' é de facto atingida * em qualquer dos casos.
Quanto ao passo (acção e progresso), é evidente que o reforço da guarda não altera a sua validade. No entanto, é instrutivo determinar de novo a acção do passo.
A acção deve garantir a veracidade da CI apesar do progresso. No início do passo admite-se que a CI é verdadeira e sabe-se que a G é verdadeira, ou seja:
CI e G: (é_primo = (Q j : 2 <= j < i : n ÷ j <> 0)) e 2 <= i <= n eé_primo e i <> nou seja,
(é_primo = (Q j : 2 <= j < i : n ÷ j <> 0)) e 2 <= i < n e é_primoou ainda,
(Q j : 2 <= j < i : n ÷ j <> 0) e 2 <= i < ne é_primoPor outro lado, no final do passo deseja-se que a CI seja verdadeira. Logo, o passo com as respectivas asserções é:
// Aqui admite-se que CI eG: (Q j : 2 <= j < i : n ÷ j <> 0) e 2 <= i < ne é_primo.Antes de determinar a acção, é conveniente verificar qual a pré-condição mais fraca do progresso que é necessário impor para que, depois dele, se verifique a CI do ciclo. Usando a transformação de variáveis correspondente à atribuição i = i + 1 (equivalente a ++i), chega-se como anteriormente a:
acção
++i;
// Aqui pretende-se que: (é_primo = (Q j : 2 <= j < i : n ÷ j <> 0)) e 2 <= i <= n.
// Aqui admite-se que CI eG: (Q j : 2 <= j < i : n ÷ j <> 0) e 2 <= i < ne é_primo.Assim sendo, a acção deve ser tal que:
acção
// (é_primo = (Q j : 2 <= j < i : n ÷ j <> 0) e n ÷ i <> 0) e 1 <= i < n,
++i;
// Aqui pretende-se que: (é_primo = (Q j : 2 <= j < i : n ÷ j <> 0)) e 2 <= i <= n.
// (Q j : 2 <= j < i : n ÷ j <> 0) e 2 <= i < n e é_primoÉ evidente, então, que a acção pode ser simplesmente:
acção
// implica (é_primo = (Q j : 2 <= j < i : n ÷ j <> 0) e n ÷ i <> 0) e 1 <= i < n.
é_primo = n % i != 0;Note-se que a acção se simplificou face à acção no ciclo com a guarda original. A alteração da acção pode ser percebida observando que, sendo a G sempre verdadeira no início do passo do ciclo, a variável é_primo tem aí sempre o valor V, pelo que a acção antiga tinha uma conjunção com a veracidade. Como V e P é o mesmo que P, pois V é o elemento neutro da conjunção, a conjunção pode ser eliminada.
A correcção da acção determinada pode ser verificada facilmente calculando a respectiva pré-condição mais fraca:
// (n ÷ i <> 0 = (Q j : 2 <= j < i : n ÷ j <> 0) e n ÷ i <> 0) e 1 <= i < n, ou seja,e observando que CI e G leva forçosamente à sua verificação:
// V = (Q j : 2 <= j < i : n ÷ j <> 0) e 1 <= i < n, ou seja,
// (Q j : 2 <= j < i : n ÷ j <> 0) e 1 <= i < n.
é_primo = n % i != 0;
// implica (é_primo = (Q j : 2 <= j < i : n ÷ j <> 0) e n ÷ i <> 0) e 1 <= i < n.
CI e G: (Q j : 2 <= j < i : n ÷ j <> 0) e 2 <= i < n e é_primoEscrevendo agora o ciclo completo tem-se:
implica (Q j : 2 <= j < i : n ÷ j <> 0) e 1 <= i < n
// PC': n >= 2* Se não lhe pareceu claro lembre-se que (A ou B) implica C é o mesmo que A implica C e B implica C. Lembre-se ainda que A e (B ou C) é o mesmo que (A e B) ou (A eC).
int i = 2;
bool é_primo = true;
// CI: (é_primo = (Q j : 2 <= j < i : n ÷ j <> 0)) e 2 <= i <= n
while(é_primo && i != n) {
é_primo = n % i != 0;
++i;
}
// CO': é_primo = (Q j : 2 <= j < n : n ÷ j <> 0)
// PC: n >= 0Mas uma observação atenta da função revela que ainda pode ser simplificada (do ponto de vista da sua escrita) para
// CO: éPrimo = ((Q j : 2 <= j < n : n ÷ j <> 0) e n >= 2)
bool éPrimo(const int n)
{
if(n <= 1)
return false;// PC': n >= 2
// CI: (é_primo = (Q j : 2 <= j < i : n ÷ j <> 0)) e 2 <= i <= n
bool é_primo = true;
for(int i = 2; é_primo && i != n; ++i)
é_primo = n % i != 0;// CO': é_primo = (Q j : 2 <= j < n : n ÷ j <> 0)
return é_primo;
}
// PC: n >= 0Este último formato é muito comum em programas escritos em C ou C++. A demonstração da correcção de ciclos incluindo saídas antecipadas no seu passo é um pouco mais complicada. Veja-se a resolução do exercício 5.a) da Aula 8 para uma versão um pouco mais eficiente desta função e para uma demonstração de correcção com saída do ciclo antecipada dentro do passo.
// CO: éPrimo = ((Q j : 2 <= j < n : n ÷ j <> 0) e n >= 2)
bool éPrimo(const int n)
{
if(n <= 1)
return false;// PC': n >= 2
// CI: (Q j : 2 <= j < i : n ÷ j <> 0) e 2 <= i <= n
for(int i = 2; i != n; ++i)
if(n % i == 0)
return false;
return true;
}
// PC: dividendo >= 0 e divisor > 0Repare-se que a CO é uma definição de divisão inteira! I.e., não só o quociente (q) multiplicado pelo divisor e somado do resto (r) tem de resultar no dividendo, como o resto tem de ser não-negativo e menor que o divisor (senão não estaria completa a divisão!), existindo apenas uma solução nestas circunstâncias.
// CO: 0 <= r < divisor e dividendo = q × divisor + r
void divisãoInteira(const int dividendo, const int divisor, int& q, int& r)
{
...
}
Como é evidente a divisão tem de ser conseguida através de um ciclo. Qual a sua CI? Neste caso, como a CO é a conjunção de três termos
CO: 0 <= r e r < divisore dividendo = q × divisor + ra solução passa por factorizar a CO.
Mas quais das proposições usar para ¬G e quais usar para CI? Um pouco de experimentação e alguns falhanços levam a que se perceba que a ¬G deve corresponder ao segundo predicado da conjunção, ou seja
G: r >= divisorDada esta escolha, qual a forma mais simples de inicializar o ciclo? É evidente que é fazendo
CI: dividendo = q × divisor + r e 0 <= r
r = dividendo;pois substituindo na CI obtém-se
q = 0;
CI: dividendo = 0 × divisor + dividendo e 0 <= dividendoe a PC garante que dividendo é não negativo.
Que progresso utilizar? O progresso deve ser tal que a guarda se torne falsa ao fim de um número finito de iteração do ciclo. Neste caso é claro que basta diminuir sempre o valor do resto para que isso aconteça. A forma mais simples de o fazer é decrementá-lo:
--r;Para que a CI seja de facto invariante, há que escolher uma acção tal que:
// Aqui admite-se que CI eG: dividendo = q × divisor + re 0 <= r e r >= divisor, ou seja,Antes de determinar a acção, verifique-se qual a pré-condição mais fraca do progresso que leva à veracidade da CI depois do progresso:
// dividendo = q × divisor + r e r >= divisor.
acção
--r;
// Aqui pretende-se que CI: dividendo = q × divisor + r e 0 <= r
// dividendo = q × divisor + r - 1 e 0 <= r - 1A acção deve ser tal que:
--r;
// Aqui pretende-se que CI: dividendo = q × divisor + r e 0 <= r
// dividendo = q × divisor + r e r >= divisor.É evidente que, em geral, não existe nenhuma acção que o consiga fazer sem alterar a variável resto! Uma observação mais cuidada das razões leva a compreender que o progresso não pode fazer o resto decrescer de 1 em 1, mas de divisor em divisor! Se assim for:
acção
// implica dividendo = q × divisor + r - 1 e 1 <= r
// dividendo = q × divisor + r e r >= divisor.Donde a acção pode ser simplesmente
acção
// dividendo = q × divisor + r - divisor e 0 <= r - divisor, ou seja,
// dividendo = (q - 1) × divisor + r e divisor <= r.
r -= divisor;
// Aqui pretende-se que CI: dividendo = q × divisor + r e 0 <= r.
++q;Tal pode ser confirmado determinando a pré-condição mais fraca da acção:
// dividendo = (q + 1 - 1) × divisor + r e divisor <= r, ou seja,e observando que CI e G implica essa pré-condição.
// dividendo = q × divisor + r e divisor <= r.
++q;
// dividendo = (q - 1) × divisor + r e 0 <= r.
Transformando o ciclo num ciclo for e colocando no procedimento:
// PC: dividendo >= 0 e divisor > 0Que também é comum ver escrito como:
// CO: 0 <= r < divisor e dividendo = q × divisor + r
void divisãoInteira(const int dividendo, const int divisor, int& q, int& r)
{
// CI: dividendo = q × divisor + r e 0 <= r
for(q = 0, r = dividendo; r >= divisor; r -= divisor)
++q;
}
// PC: dividendo >= 0 e divisor > 0onde se colocou a acção no progresso do for.
// CO: 0 <= r < divisor e dividendo = q × divisor + r
void divisãoInteira(const int dividendo, const int divisor, int& q, int& r)
{
// CI: dividendo = q × divisor + r e 0 <= r
for(q = 0, r = dividendo; r >= divisor; r -= divisor, ++q)
;
}
Note-se que a vírgula usada para separar o progresso e a acção do ciclo é o operador de sequenciamento do C++. Esse operador garante que os seus primeiro operando é calculado antes do segundo operando, e tem como resultado o valor do segundo operando. Por exemplo, as instruções:
int n;colocam o valor 4 na variável n.
n = (1, 2, 3, 4);
1. Desenvolva uma função que calcule, de uma forma iterativa, o factorial de um inteiro passado como argumento. Compare com a versão recursiva desenvolvida anteriormente.
2. Implemente versões iterativa e recursiva de funções que devolvam o n-ésimo termo da sucessão de Fibonacci. Esta sucessão é definida recorrentemente por:
F0 = 0Teste ambas as funções utilizando o programa dado abaixo. Dê o nome fib ao ficheiro executável.
F1 = 1
Fn = Fn-1 + Fn-2, se n > 1
using namespace std;
long int fibonacciRecursiva(int
n)
{
// a
completar...
}
long int fibonacciIterativa(int
n)
{
// a
completar...
}
/*
Para testar
este programa deve executá-lo na janela de comandos
com um argumento
inteiro positivo (de preferência menor que 35) ou
em modo de
depuração dando a instrução:
set arg 30
(ou outro número
inteiro positivo
menor que 35) antes da instrução
r(un).
*/
int main(int numero_de_argumentos,
char* argumentos[])
{
if(numero_de_argumentos
!= 2) {
cerr << "Utilização: " << argumentos[0]
<< " inteiro" << endl;
return 1;
}
int n = atoi(argumentos[1]) + 1;
cout.precision(6);
for(int i
= 0; i != n; i++) {
cout << "Fibonacci(" << i << ") = "
<< fibonacciIterativa(i);
const int repeticoesIterativa = 1000000 / (i + 1) + 1;
const int repeticoesRecursiva =
int(1000000 / pow((1.0 + sqrt(5)) / 2.0, i)) + 1;
clock_t t = clock();
for(int j = 0; j != repeticoesRecursiva; ++j)
fibonacciRecursiva(i);
t = clock() - t;
cout << ", recursiva "
<< t / double(CLOCKS_PER_SEC) / repeticoesRecursiva * 1000.0
<< " ms";
t = clock();
for(int j = 0; j != repeticoesIterativa; ++j)
fibonacciIterativa(i);
t = clock() - t;
cout << ", iterativa "
<< t / double(CLOCKS_PER_SEC) / repeticoesIterativa * 1000.0
<< " ms" << endl;
}
}
fib 37 | awk '{print $5, $8}' > ! tempos ; echo "set xlabel 'n'; set ylabel 'tempo [ms]'; set xtics 1; set grid; set logscale y; set ytics 0.0001,1.584893192,10000; plot 'tempos' using 2 title 'iterativa' with lines, 'tempos' using 1 title 'recursiva' with lines; pause -1" > ! g ; gnuplot g ; rm -f g tempos3. Complete o procedimento void leLinha(string& linha), do programa abaixo, de modo a que permita ao utilizador inserir caracteres até que este introduza o caracter '\n', que corresponde a um fim-de-linha. Esses caracteres devem ser guardados na cadeia de caracteres passada por referência, que deve ser limpa antes da leitura começar.
Para resolver este problema precisar de saber que:
using namespace std;
void leLinha(string& linha)
{
// a
completar...
}
int main()
{
cout <<
"Introduza o seu nome (completo): ";
string primeiro_nome;
cin >> primeiro_nome
>> ws;
string apelidos;
leLinha(apelidos);
cout <<
"O seu nome é " << primeiro_nome << " " << apelidos
<< endl;
}
5.a) Sabendo que todos os números primos maiores que 3 se podem escrever na forma 6 × m - 1 ou 6 × m + 1 (mas nem todos os números desta forma são primos!) uma função que devolva true se o valor do argumento inteiro for primo e false no caso contrário.
5.b) Desenvolva um programa que escreva no ecrã todos os números primos entre 2 e n (inclusivé), sendo n dado pelo utilizador.
5.c) Sabendo que todos os números primos maiores que 3 se podem escrever na forma 6 × m - 1 ou 6 × m + 1 (mas nem todos os números desta forma são primos!), torne o programa da alínea anterior mais eficiente.
6.a) Faça um procedimento que imprima no ecrã um quadrado com a altura indicada como argumento e com o interior vazio. Crie um pequeno programa para testar o procedimento. Exemplo:
Introduza a altura do quadrado: 46.b) Faça um procedimento que imprima no ecrã um quadrado com a altura indicada como argumento e com as diagonais assinaladas. Crie um pequeno programa para testar o procedimento. Exemplo:
****
* *
* *
****
Introduza a altura do quadrado: 87. Faça uma função que permita ao utilizador inserir 20 caracteres e devolva quantos dos caracteres introduzidos pelo utilizador são asteriscos. Crie um pequeno programa para testar esta função. Exemplo:
********
** **
* * * *
* ** *
* ** *
* * * *
** **
********
Introduza um conjunto de caracteres: qwe*98*8wer*we112rwq8. Escreva uma função que calcule a multiplicação inteira de dois números recorrendo apenas aos operadores aritméticos + e -. Qual é o progresso mais simples? E o mais eficiente?
Contei 3 asteriscos.
9. Suponha que as letras A, B, C e D foram codificadas em zeros e uns da seguinte forma: A = 0, B = 11, C = 100 e D = 101. Crie um programa que, quando é introduzida uma sequência de zeros e uns apartir do teclado, descodifique as várias letras. Atenção: pode haver sequências que não terminam com a codificação total de um caracter (por exemplo 01 = A?). O programa deve estar preparado para lidar com esse tipo de erros do utilizador. Por exemplo:
Introduza um conjunto de zeros e uns: 10010011001101Utilize uma função para descodificar cada caractere. A leitura deve terminar quando for introduzido um caractere que não seja '0' nem '1'.
CCBAABA?
10. Crie uma função que leia uma sequência de números inteiros e devolva um valor booleano que indica se este conjunto de números está por ordem crescente (no sentido lato). A sequência termina quando o utilizador insere o número 0 (zero). Como é evidente este número serve apenas como marcador do fim da sequência e não é tido em conta para o resultado da função. Pode assumir que a sequência tem sempre dois ou mais números. Crie um pequeno programa para testar esta função.
11. Crie uma função que leia uma sequência de números inteiros e devolva um valor inteiro que será 2 caso a sequência esteja ordenada por ordem crescente (em sentido lato), 1 caso esteja por ordem decrescente (em sentido lato), 0 (zero) caso seja constante e -1 caso não seja monótona. A sequência termina quando o utilizador insere o número 0 (zero). Como é evidente este número serve apenas como marcador do fim da sequência e não é tido em conta para o resultado da função. Crie um pequeno programa para testar esta função.
[2] Yedidyah Langsam, Moshe J. Augenstein e Aaron M. Tenenbaum, "Data Structures Using C and C++", segunda edição, Prentice Hall, Upper Saddle River, New Jersey, 1996.
[3] Donald E. Knuth, "Fundamental algorithms", volume 1 de "The Art of Computer Programming", segunda edição, segunda edição, Addison-Wesley Publishing Company, Reading, Massachusetts, 1973. *
[4] David Gries, "The Science of Programming", volume da série "Texts and Monographs in Computer Science", editada por David Gries, Springer-Verlag, Nova Iorque, 1981 [1989]. *
[5] Edsger Dijkstra, "A Discipline of Programming", Prentice Hall, 1976. *
[6] Bjarne Stroustrup, "The C++ Programming Language", terceira edição, Addison-Wesley, Reading, Massachusetts, 1998. *